Besoin d'aide dans la densite...

Soit A c R verifiant :
V xeR, E a,b e A, a<x<b
V a,b e A. (a+b)/2 e A

E: il existe V: pour tout e: appartient

Montrer que A est dense dans R.

Merci...

Soit
2
f :N2 →N,
(p,q) 􏰀→ (1/2)(p+q)(p+q+1)+ p

1. Montrer pour q>0: f(p+1,q−1)= f(p,q)+1et f(0,p+1)= f(p,0)+1.
2. Montrerque: f(0,p+q)≤ f(p,q)< f(0,p+q+1).
3. Montrer que g : n 􏰀→ f (0, n) est strictement croissante.
4. Montrer que f est injective (on supposera f(p,q) = f(p′,q′) et on montrera dans un premier temps que p+q = p′ +q′).
5. Montrer que f est surjective.

Grinta a écrit:

Soit A c R verifiant :
V xeR, E a,b e A,  a<x<b
V a,b e A. (a+b)/2 e A
E: il existe V: pour tout e: appartient
Montrer que A est dense dans R.
Merci...

Je propose une solution:
Soient x un réel.
Selon l'hypothèse, on a .
Donc , où I=][.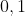
On va construire une suite d'éléments de qui converge vers x.
On a: 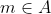, et 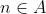, donc 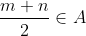, et par suite .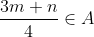
On généralise ce résultat tout en démontrant que: , et cela par récurrence simple sur l'entier k.
On démontre aussi que , et cela par par récurrence sur l'entier p.
On doit donc choisir p en fonction de k, tel que la suite 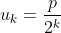, admet t comme limite lorsque k tend vers .
On considère la suite d'éléments de A, définie par: (E désigne la fonction partie entière).
Cette suite converge vers x, lorsque k tend vers .
CQFD.
Sauf erreurs.

Le deuxieme cas, ce n'est pas plutot p=<n ??

Bonne solution nmo . mais juste une remarque il s'agit ici du principe du dicotomie.
Puisque  a<x<b alors soit  a<x<(a+b)/2 ou  (a+b)/2<x<b on iterant cette operation on constate que la difference entre x et les bornes des intervalles qui vont etre definie successivement diminue .
D'ou l'idee de considere dans un premier lieu la suite
u_0=(a+b)/2 et u_1=b et u_(n+2)=(u_n+u_(n+1))/2 et la suite en decoule .