ipek
Habitué

 Nombre de messages : 26 Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
 |  Sujet: exercice difficile Sujet: exercice difficile  Mer 01 Jan 2014, 15:11 Mer 01 Jan 2014, 15:11 | |
| j'arrive pas à résoudre cet exercice .. ça fait 2 semaines que je cherche la solution  soit a et b et c strictement positif démontrez que √(2a)⁄√(a+b) +√(2b)⁄√(b+c) + √(2c)⁄√(a+c)≤3 | |
|
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  Mer 01 Jan 2014, 19:10 Mer 01 Jan 2014, 19:10 | |
| réponse: on sait que la moyenne quadratique est supérieur ou égale la moyenne arithmétique alors:  alors il suffit maintenant de prouver que 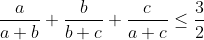 par symétrie de rôle on suppose que 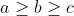 avec l'inégalité de réordonnement on aura  et  en ajoutant les deux inégalité on aura  alors 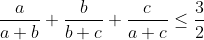 | |
|
ipek
Habitué

 Nombre de messages : 26 Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  Mer 01 Jan 2014, 21:46 Mer 01 Jan 2014, 21:46 | |
| merci pour votre réponse
mais normalement je pense on doit d'abord démontrer la première inéquation
| |
|
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  Mer 01 Jan 2014, 21:49 Mer 01 Jan 2014, 21:49 | |
| j'ai pas écrit toutes les simplifications, mais juste les résultats parce que cela prend du temps d'une part, d'autre part c'est évident.
P.S elle ne s'appelle pas inéquation c'est inégalité on cherche pas un inconnu
Dernière édition par L-W-P le Jeu 02 Jan 2014, 00:50, édité 1 fois | |
|
ipek
Habitué

 Nombre de messages : 26 Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  Mer 01 Jan 2014, 21:55 Mer 01 Jan 2014, 21:55 | |
| ok merci  donc je vais essayer de la refaire | |
|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  Jeu 02 Jan 2014, 19:55 Jeu 02 Jan 2014, 19:55 | |
| - L-W-P a écrit:
- par symétrie de rôle on suppose que
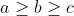
On aura:  Cela est clairement faux, si on prend 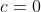 et 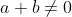 . L'inégalité que tu as écrit devient: 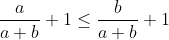 , soit 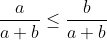 ou encore 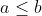 . Et cela contredit ce que tu as supposé. | |
|
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  Jeu 02 Jan 2014, 20:28 Jeu 02 Jan 2014, 20:28 | |
| Proposition , on pose x=b\a , y=c\b , z=a\c ; on utilise l'estimation suivante , rac(u)+rac(v) =< rac(2(u+v)} facile a prouvé en élévant au carré ou bien c'est simplement caushy swarsh pour les connaisseur , l'inégalité est equivalente apres le changemente de variable a : \sum 1\rac(1+x) =< 3\rac(2) , parmis les produites xy , yz , xz il existe au moin un inférieur a 1 , sans perdre de généralité on peut supposé xy =< 1 . d'apres l'estimation on a : &space;.) en utilise le lemme suivant maintenant , facile a prouver aussi par simple calcule , pour u , v positif tel que uv =< 1 on a : 1\1+u² + 1\1+v² =< 2\1+uv . il vient donc en l'appliquant au membre droit de l'estimation que :  comme xy=1\z , en posant z=m² il suffit de prouver que ,  , ce qui est vrai je te laisse faire les calcules  , bonne chance . | |
|
Contenu sponsorisé
 |  Sujet: Re: exercice difficile Sujet: Re: exercice difficile  | |
| |
|
