Exo Tc

pour le 1:
A=1+2+3+...+n
A=n+(n-1)+(n-2)+...+1
2A=n+1+(n-1)+2+(n-2)+3+...+n+1
2A=n+1+n+1+n+1.....+n+1
2A=n(n+1)
A=[n(n+1)]/2

egalite 2, Indication

Spoiler:

J'ai été vraiment très intéressé par cet exercice, surtout qu' il a été proposé par M. Legend_Crush: Les sommes des puissances sont très utiles dans de nombreux exercices et en facilitent la résolution, et pour ceux qui sont intéressés voici un lien qui donne une très bonne introduction pour le calcul des sommes des nombres entiers naturels grâce aux nombres de Bernouilli :
http://fr.wikipedia.org/wiki/Nombre_de_Bernoulli

Quant à l'exercice proposé, voici une solution dont la démarche se trouve dans de nombreux recueils mathématiques et qui peut être généralisée.

J'aimerai bien que M. Legend_Crush, me rassure sur l'exactitude du résultat que j'ai obtenu pour la deuxième inégalité.

Merci.

En fait, pour la premier somme ya un million (hyperbole :p ) de méthode parmi lesquelles:
   1* S=1+2+...+n
       S=n+(n-1)+...+1
==>  2S=n(n+1) => S=n(n+1)/2

   2*  la méthode que vous avez proposé

   3* considérer un polynôme de degré 2 tq: P(x+1)-P(x)=x , déterminer le polynome,puis téléscoper
   4* Réccurence <3
Pour la deuxième, je ne connais que 2 méthode, l'une est celle que vous avez uitlisé, la réccurence puis celle de considérer un polynome de degré 3 tq P(x+1)-P(x)=x² ...

Pour la première inégo, vous l'avez parfaitement résolu.
Pour la deuxième, au lieu de devellopper, j'ai pensé à faire comme suit:

Merci M. Legend_Crush, Je n'aurai jamais pensé à développer (2n + 1) en (n + n + 1): c'est une très jolie astuce que je viens de découvrir: Merci.

Ah alors l'inégalité n'est pas aussi bonne que je le voulais, je viens de m'en rendre compte, ça doit être alors 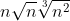. c'est moi qui a fait cet exo :p (s'il existait pas avant)

jallais le dire mais comme n^2>=n ca en decoule (comme n est un entier)

Salam,
Voici une autre démonstration.

http://www.4shared.com/office/k3hPoouFce/Demonstration_-_arabmaths.html

M. Mae24, j'ai le regret de vous faire remarquer que le lien présumé de la "Démonstration" mène vers une page qui n'a aucune parenté avec les Mathématiques.

Salam,
Tu vas trouver sur ce lien un document que tu peux télécharger.