P.Coelho
Habitué

 Nombre de messages : 17 Nombre de messages : 17
Age : 27
Localisation : berchide
Date d'inscription : 28/02/2014
 |  Sujet: Joliii Sujet: Joliii  Dim 02 Mar 2014, 11:58 Dim 02 Mar 2014, 11:58 | |
| Trouver tous les entiers n tels que 2^(n-1) divise n! | |
|
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Joliii Sujet: Re: Joliii  Dim 02 Mar 2014, 12:34 Dim 02 Mar 2014, 12:34 | |
| on a clairementt - Spoiler:
n=2^a avec a de N
je posterais la solution complete plus tard
| |
|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Joliii Sujet: Re: Joliii  Dim 02 Mar 2014, 12:35 Dim 02 Mar 2014, 12:35 | |
| Il nous faut montrer que les puissances deux sont les seules solutions. Dans un premier temps, on va montrer qu'elle le satisfaissent vraiment puis, on démontrera qu'elle sont les seules. J'userai dans ma démo le théo. de Legendre:   d'ou 2^{n-1} ne peut diviser n! si n n'est pas une puissance de 2 Conclusion: S={2^k /kCN*} | |
|
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Joliii Sujet: Re: Joliii  Mer 05 Mar 2014, 23:21 Mer 05 Mar 2014, 23:21 | |
| bien joué ^^ mais peux-tu m'expliquer le premier passage stp? je crains ne pas avoir compris :2^(n-1)|n! <==> [2^k/2]....  merci bien de m eclairer | |
|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Joliii Sujet: Re: Joliii  Mer 05 Mar 2014, 23:51 Mer 05 Mar 2014, 23:51 | |
| 2^(n-1)|n! <=> n-1 =< V_2(n!) et j'ai remplacé V_2(n!) par l'expression de Legendre  Amicalement | |
|
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Joliii Sujet: Re: Joliii  Jeu 06 Mar 2014, 07:26 Jeu 06 Mar 2014, 07:26 | |
| j'ai compris. merci bien  | |
|
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Joliii Sujet: Re: Joliii  Jeu 06 Mar 2014, 13:09 Jeu 06 Mar 2014, 13:09 | |
| voila une autre methode plus courte, basee sur la tienne (tout les honneurs te reviennent biensur) 2^(n-1) | n!  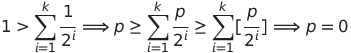 ce qui donne le resultat demandé L-C, a toi de poster un exo  | |
|
