lim E(x)^E(x)

Sauf Erreur, . je sais que j'ai utilisé des écritures pas acceptée ....
Si mes calculs de ces limites sont correctes, Mtn je vous invite à calculer une limite (si elle existe) qui m'est venue à l'esprit à l'instant :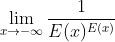

c est 0 ^^

elidrissi a écrit:

c est 0 ^^

celle-là 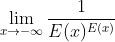?? O.o

euuh oui celle la. jai calculé ici avant de demontré [lien mais malheureusement pas pu demontrer

elidrissi a écrit:

euuh oui celle la. jai calculé ici avant de demontré [lien mais malheureusement pas pu demontrer

Je ne vois pas pourquoi ce serait 0. Déja la limite que je vois dans ton lien est alors que j'ai donné 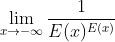. Je pense que cette limite que j'ai donné n'existe pas, car sa vire périodiquement de +oo à -oo selon si E(x) est pair ou impair. A vous de voir si c'est correct ^^

oui tu dois remplacer en haut par la fonction souhaitee.
je le pense aussi, mais je crois qu un programme se connait surement mieux que moi . quand la limite n existe pas il affiche un message d erreur...franchement je ne sais pas

Si j'ai bien compris le cours, et à notre niveau, la fonction f qui à x fait correspondre f(x)=x^x , n'est défini que sur ]0;+infini[, donc chercher la limite de E(x)^E(x) quand x tend vers -infini est absurde à notre niveau, de même pour la limite de 1/(E(x)^E(x)) quand x tend vers -infini.

A un niveau supérieur, comme on me l'a indiqué, on peut représenter par exemple x^x sur http://www.wolframalpha.com/ : on entre dans l'etude des fonctions à variables complexes.

Att, Je pense que E(x)^E(x) est définie sur R, car aussi je suppose que l'ensemble de definition de x^x inclus également Z*-
Donc pourquoi n'aurait-elle pas de limite en -oo ?

Vous avez raison M. Legend_Crush, E(x)^E(x) a une limite quand x tend vers -infini, mais en ce qui concerne l'ensemble de définition de x^x, j'ai un autre avis : je crois qu'il n'inclue pas Z*-.

Somme toute, je vous laisse juger de l'exactitude de ma proposition, avec tous mes remerciements.