| | x^y +y^x |  |
|
|
| Auteur | Message |
|---|
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: x^y +y^x Sujet: x^y +y^x  Mar 04 Mar 2014, 22:51 Mar 04 Mar 2014, 22:51 | |
| Bonsoir , x et y des réels positifs . montrez que x^y+y^x>1 Amicalement.  | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Jeu 06 Mar 2014, 13:33 Jeu 06 Mar 2014, 13:33 | |
| J'ai bien aimé cet exercice qui m'a fait faire des recherches durant deux jours, je vous en remercie beaucoup.  | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Jeu 06 Mar 2014, 13:37 Jeu 06 Mar 2014, 13:37 | |
| On considère WLog x>y donc x=y+k (k de R+) Donc il faut montrer (f)  On a  Donc f est croissante, il s'en suit que: 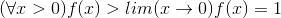 Et donc : 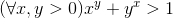 | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Jeu 06 Mar 2014, 13:47 Jeu 06 Mar 2014, 13:47 | |
| | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Jeu 06 Mar 2014, 14:00 Jeu 06 Mar 2014, 14:00 | |
| Une autre solution pour le plaisir:
Cas n° 1: x ou y >= 1
Démarche similaire à celle explicité dans ma solution sus mentionnée.
Cas n° 2: x,y<1
par l'inégalité de Bernoulli, nous avons :
x^y = [1 + (x-1)]^y >= 1 + y(x-1) => x^y + y -1 >= xy ,
de même on a:
y^x + x - 1 >= xy ,
donc on a x^y + y^x + x + y - 2 >= 2xy
équi x^y + y^x>= 2xy - x - y + 2 =(xy - x - y + 1) + xy + 1 = (1 - x)(1 - y) + xy + 1 > 1
donc , x^y + y^x > 1 .
Donc quelque soient x et y des réels positifs, on a : x^y + y^x > 1 .
Une remarque: j'ai utilisé principalement du "vert" dans ma première solution en l'honneur à M. Bianco_Verde qui veut dire peut-être "Blanc et Vert".
Merci. | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Sam 08 Mar 2014, 08:46 Sam 08 Mar 2014, 08:46 | |
| | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mar 11 Mar 2014, 21:09 Mar 11 Mar 2014, 21:09 | |
| Je crois que la solution de MR. Elidrissi est fausse vu que l'inégalité de BERNOULLI est employée d'une maaniere incorrecte. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mer 12 Mar 2014, 07:04 Mer 12 Mar 2014, 07:04 | |
| en effet, je crois qu elle est a l envers
mais ce nest pas ma solution. je l ai trouvée dans le livre de Cvetkovski Z. | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mer 12 Mar 2014, 18:41 Mer 12 Mar 2014, 18:41 | |
| Pouvez vous nous donner le lien du livre en format pdf ?? ^^ | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mer 12 Mar 2014, 20:53 Mer 12 Mar 2014, 20:53 | |
| Je n'ai plus le lien, je m en excuse. mais le nom est :
inequalities theorems techniques and selected problems springer 2012 | |
|
  | |
naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mer 02 Mai 2018, 19:29 Mer 02 Mai 2018, 19:29 | |
| | |
|
  | |
naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mer 02 Mai 2018, 20:26 Mer 02 Mai 2018, 20:26 | |
| : حيث إن
، (1+x)^r > 1+r.x
x> -1 و r>1لكل : فإنَّ
، (1-x)^(1/r) > 1-x/r
0<r<1 و x<1لكل :أي ،[(1-x)^(1/r)]^r > (1-x/r)^r
1-x> (1-x/r)^r : يعني | |
|
  | |
naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  Mar 15 Mai 2018, 15:14 Mar 15 Mai 2018, 15:14 | |
| - naïl a écrit:
: حيث إن
، (1+x)^r > 1+r.x
x> -1 و r>1لكل : فإنَّ
، (1-x)^(1/r) > 1-x/r
0<r<1 و x<1لكل :أي ،[(1-x)^(1/r)]^r > (1-x/r)^r
1-x> (1-x/r)^r : يعني x<=r لكن يجب لصحة المتفاوتة الأخيرة أن يكون الطرف الأدنى موجبا أي .x عوض x*r و للحصول على المتفاوتة المبتغاة يجب وضع https://mathsmaroc.jeun.fr/f26-theoremes-et-formules انظر قسم القواعد و المتطابقات | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: x^y +y^x Sujet: Re: x^y +y^x  | |
| |
|
  | |
| | x^y +y^x |  |
|
