| | Test n°3 Olympiade TSM 2014 |  |
|
|
| Auteur | Message |
|---|
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Test n°3 Olympiade TSM 2014 Sujet: Test n°3 Olympiade TSM 2014  Ven 21 Mar 2014, 12:39 Ven 21 Mar 2014, 12:39 | |
| Exercice 1 :Peut-on écrire le nombre 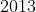 sous forme 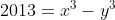 où 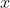 et 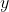 sont des nombres entiers relatifs ? Exercice 2 :Trouver toutes les fonctions surjectives 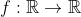 telles que 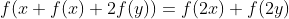 pour tout 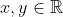 . Exercice 3 :Soient 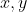 et  trois nombres réels strictement positifs tels que : 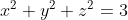 Montrer que : 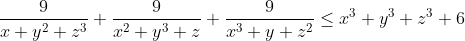 Exercice 4 : Exercice 4 :Soit ABC un triangle à angles aigus avec 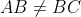 , M le milieu du côté [ AC], N le point où la médiane ( BM) rencontre à nouveau le cercle circonscrit au triangle ABC, H l'orthocentre du triangle ABC, D le point sur le cercle circonscrit pour lequel l'angle 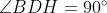 et K le point tel que ANCK est un parallélogramme. Montrer que les droites ( AC),( KH) et ( BD) sont concourantes. | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: Test n°3 Olympiade TSM 2014 Sujet: Re: Test n°3 Olympiade TSM 2014  Ven 21 Mar 2014, 12:39 Ven 21 Mar 2014, 12:39 | |
| Pour moi voici ce que j'ai fais : - Solutions :
- Exercice 1 :
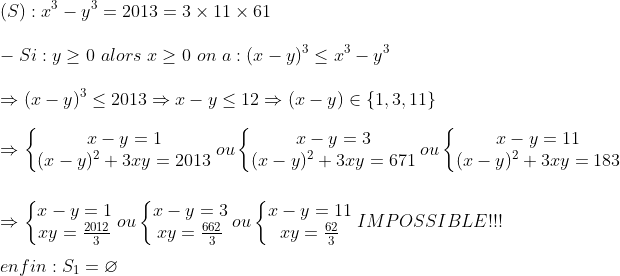 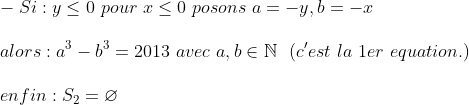 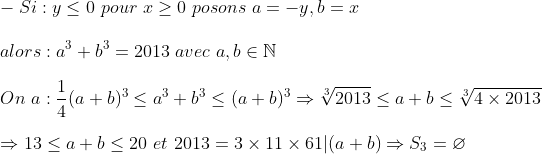 (je vois que les inégalités sont importants  ) Conclusion : Il n'existe aucun couple (x,y) qui vérifie les données de l'exercice.
- Exercice 2 :
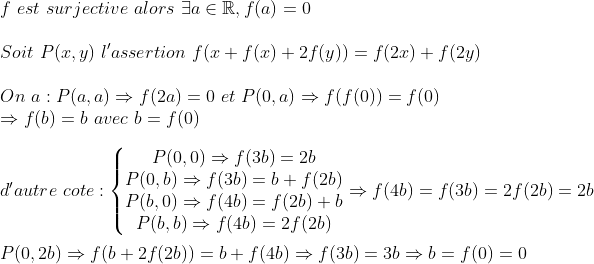 bon les choses importants que j'ai trouvée ce sont : 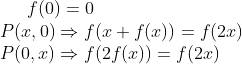 Cela signifie que l'exercice n'est pas encore été résolu  . Je pense que c'est un bon exo!!
- Exercice 3 :
- Exercice 4 :
est déjà posté l'année précèdent ici https://mathsmaroc.jeun.fr/t19869-olampide-968830-11-2012-9688 mais sans solution mais je l'ai trouvée facile, il suffit de connaître quelques relations posons :- 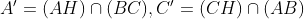 - 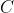 le cercle circonscrit au triangle ABC - 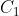 le cercle circonscrit au triangle AHC - 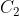 le cercle circonscrit au quadrilatère A'BC'H.  " K le point tel que ANCK est un parallélogramme" et " M le milieu du côté [ AC]" 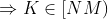 et M le milieu de [ NK] On a alors : 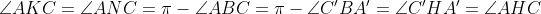 ce qui nous a donne que 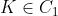 d'autre côté 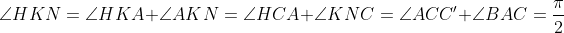 d'où : 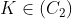 Résumé : 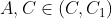 ; 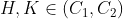 ; 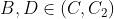 Conclusion : les droites ( AC),( KH) et ( BD) sont concourantes.
| |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Test n°3 Olympiade TSM 2014 Sujet: Re: Test n°3 Olympiade TSM 2014  Ven 21 Mar 2014, 15:36 Ven 21 Mar 2014, 15:36 | |
| Pour l'exercice 1, on a 2013 = x^3 - y^3 = (x - y)((x - y)^2 + 3 xy)= (x - y)^3 + 3 xy(x - y) , donc on a xy = (2013 - (x - y)^3)/(3(x - y)) qui doit être un entier relatif.
Les diviseurs de 2013 sont: 1; 3; 11; 61; 33; 183; 671; 2013 et leurs conjugués, donc (x - y) peut prendre l'une de ces valeurs, et par simple calcul on obtient que (2013 - (x - y)^3)/(3(x - y)) n'est pas un nombre entier relatif, donc 2013 ne peut pas s'écrire sous la forme d'une différence de cubes d'entiers relatifs.
J'ai proposé cette solution pour inviter tous les amis à apporter de l'aide - dans la limite du possible - à M. Komikomi qui a des difficultés pour résoudre un exercice sur les rotations dans un plan complexe.
Merci.
| |
|
  | |
Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Test n°3 Olympiade TSM 2014 Sujet: Re: Test n°3 Olympiade TSM 2014  Ven 21 Mar 2014, 17:08 Ven 21 Mar 2014, 17:08 | |
| | |
|
  | |
Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Test n°3 Olympiade TSM 2014 Sujet: Re: Test n°3 Olympiade TSM 2014  Ven 21 Mar 2014, 17:25 Ven 21 Mar 2014, 17:25 | |
| Pour la 1er qestion , j'ai pas compris le passage où x-y=< alors x-y £ (1,3,11)  | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: Test n°3 Olympiade TSM 2014 Sujet: Re: Test n°3 Olympiade TSM 2014  Ven 21 Mar 2014, 22:52 Ven 21 Mar 2014, 22:52 | |
| - Amiral a écrit:
- Pour la 1er qestion , j'ai pas compris le passage où x-y=< alors x-y £ (1,3,11)
 On a 2013=(x-y)(x²+xy+y²) donc 0 <x-y <12 les diviseurs de 2013 qui appartiens a [0,12] sont 1,3 et 11 alors x-y £ (1,3,11). | |
|
  | |
Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: Test n°3 Olympiade TSM 2014 Sujet: Re: Test n°3 Olympiade TSM 2014  | |
| |
|
  | |
| | Test n°3 Olympiade TSM 2014 |  |
|
