nmo
Expert sup
 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 | | Sujet: Inégalité: Sam 13 Sep 2014, 10:52 | |
| Voici une inégalité qui n'est pas classique: Montrez que:  [ 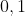 ]  :\cos(x)\ge e^{-x^2}) . Bonne chance.P.S: On pet étendre le résultat sur [  ] pour des raisons de parité.
Dernière édition par nmo le Dim 14 Sep 2014, 12:20, édité 2 fois | |
|
galillee56
Expert grade2
Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
| | Sujet: Re: Inégalité: Dim 14 Sep 2014, 00:09 | |
| - Spoiler:
deriver f(x)=exp(x^2)*cos(x) et montrer que tan(x)-2x est negative sur [0,1] conclure quef est croissante sur [0,1]
| |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Inégalité: Dim 14 Sep 2014, 12:19 | |
| - galillee56 a écrit:
- Spoiler:
deriver f(x)=exp(x^2)*cos(x) et montrer que tan(x)-2x est negative sur [0,1] conclure quef est croissante sur [0,1]
J'ai une autre démonstration en tête autre que celle que tu as adoptée. Sinon, comment tu vas démontrer que [ 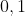]  :\tan(x)-2x\le0) ? | |
|
galillee56
Expert grade2
Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
| | Sujet: Re: Inégalité: Dim 14 Sep 2014, 12:30 | |
| f(x)=tan(x)-2x f'(x)=tan^2(x)-1 donc f decroissante sur [0,pi/4] et croissante sur [pi/4,1] tan(1)<2 d'ou le resultat | |
|
younesmath2012
Expert sup
Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
| | Sujet: Re: Inégalité: Dim 14 Sep 2014, 18:58 | |
| | |
|
