| | belle équation trigo |  |
|
|
| Auteur | Message |
|---|
belgacem
Maître
 Nombre de messages : 112 Nombre de messages : 112
Age : 61
Date d'inscription : 18/06/2012
 |  Sujet: belle équation trigo Sujet: belle équation trigo  Ven 16 Jan 2015, 19:48 Ven 16 Jan 2015, 19:48 | |
| Résoudre dans R l'équation suivante : 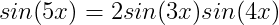 | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Lun 19 Jan 2015, 13:16 Lun 19 Jan 2015, 13:16 | |
| - belgacem a écrit:
- Résoudre dans R l'équation suivante :
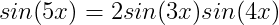 BJR belgacem En effet , c'est Une Belle Equation Trigo !! Mais la Poser ne Signifie pas que l' on sache la résoudre à la Main aussi facilement que Cela !!!! Maple ou Mathématica Sauront le faire en un Clin d' Oeil . LHASSANE PS1 : Pour des Lycéens , ce n'est pas Intéressant du tout .... PS2 : Pour les Etudiants en Fac et les Préparationnaires , c'est un excellent T.P à faire sur Maple ou tout autre Logiciel de Calcul Formel !!! PS3 : Pour Toi belgacem , Tu pourras essayer celle-ci un peu moins dure Résoudre dans R l'équation suivante : 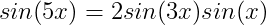
Dernière édition par Oeil_de_Lynx le Sam 07 Fév 2015, 13:10, édité 1 fois | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Mar 03 Fév 2015, 19:59 Mar 03 Fév 2015, 19:59 | |
| On a Sin(5x) est une fonction impaire et 2 Sin(3x) Sin(4x) est une fonction paire: l'égalité n'a lieu que
pour (Sin(5x)=0 et Sin(3x) Sin(4x)=0) <--> (Sin(5x)=0 et Sin(3x)=0) ou (Sin(5x)=0 et Sin(4x)=0)
<--> (5x=k pi : k entier relatif et 3x=h pi : h entier relatif)
ou (5x=m pi : m entier relatif et 4x=n pi : n entier relatif)
<--> (x=k pi/5 : k entier relatif et x=h pi/3 : h entier relatif) : k=3K et h=5H avec K et H des entiers relatifs
ou (x=m pi/5 : m entier relatif et x=n pi/4 : n entier relatif) : m=4M et n=5N avec M et N des entiers relatifs
<--> (x=K pi : K entier relatif et x=H pi : H entier relatif)
ou (x=M pi : M entier relatif et x=N pi : N entier relatif)
<--> x= t pi : t entier relatif.
J'espère que ce n'est pas faux.
Cordialement, AymaneMaysae. | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Mar 03 Fév 2015, 20:22 Mar 03 Fév 2015, 20:22 | |
| - aymanemaysae a écrit:
- On a Sin(5x) est une fonction impaire et 2 Sin(3x) Sin(4x) est une fonction paire: l'égalité n'a lieu que
pour (Sin(5x)=0 et Sin(3x) Sin(4x)=0) <--> (Sin(5x)=0 et Sin(3x)=0) ou (Sin(5x)=0 et Sin(4x)=0)
.........................................................................
J'espère que ce n'est pas faux.
Cordialement, AymaneMaysae. BSR au Forum . BSR aymaneMaysae . C'est Très Séduisant à Première Vue ... Mais Vous Faites Une Erreur . Considérons les deux applications suivantes : f : x ---------> f(x)=x^2 de IR dans IR et g : x ---------> g(x)=x.Abs(x) de IR dans IR aussi f est PAIRE , g est IMPAIRE Mais on a l' égalité f(x)=g(x) lorsque x est dans IR+ Et non pas seulement en x=0 . Voilà votre erreur . Autrement , c'est très charmant . Amicalement . LHASSANE | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Mar 03 Fév 2015, 23:37 Mar 03 Fév 2015, 23:37 | |
| Merci, pour la remarque.
Je me rends compte que ce n'est pas si simple que çà !
| |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Mer 04 Fév 2015, 20:35 Mer 04 Fév 2015, 20:35 | |
| | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Mer 04 Fév 2015, 21:37 Mer 04 Fév 2015, 21:37 | |
| Résoudre dans R l'équation suivante : 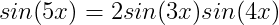 BSR au Forum . BSR aymanemaysae . Mon idée était de transformer tout le problème en une recherche de racines d' un polynôme P(SIN(x)) . Or si SIN(5.x) et SIN(3.x) peuvent s'exprimer sous la forme Q(SIN(x)) ou Q[X] est un polynôme facile à déterminer ... Le Cas de SIN(4.x) pose problème La Transformation de SIN(4x) fait apparaitre un facteur COS(x) gênant ..... Il n' empêche que l' on peut continuer en Tournant la difficulté MAIS en compliquant les Calculs . Il suffira de poser t=TAN(x/2) et d' utiliser les Formules Classiques : SIN(x) = 2.t/(1+t^2) et COS(x) = (1-t^2)/(1+t^2) Pour ramener l' équation initiale à une autre de la forme : Résoudre dans IR l' équation R(t)=0 Avec R[X] polynôme ( de degré assez élevé , je n' ai pas cherché ... ) Cela ne me parait pas évident à traiter ..... Amicalement . LHASSANE | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Jeu 05 Fév 2015, 16:15 Jeu 05 Fév 2015, 16:15 | |
| | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Sam 07 Fév 2015, 13:07 Sam 07 Fév 2015, 13:07 | |
| BJR au Forum.
BJR AymaneMaysae .
Je voulais te dire Trois choses :
1) Les expressions de SIN(5x) , SIN(3x) et SIN(4x) sont exactes ...
2) L'équation proposée admet les solutions x=0 Modulo (PI)
A Cause du Facteur SIN(x) que l' on retrouve ......
3) Lorsque SIN(x)<>0 on peut simplifier l' équation d' une part et d' autre par et on peut se permettre de faire le Changenent de variable t=TAN(x/2)
Note que Modulo PI , il n'est valable que si -PI <x < PI .
Pour le reste , le polynôme en t obtenu est de Degré si élevé qu' Il faut laisser Maple ou Mathématica utiliser ses Routines Internes pour trouver les autres solutions Modulo PI .
Les Calculs à la Main s' avèrent extrêmement Fastidieux !!!!!
Amicalement . LHASSANE
| |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  Mer 24 Juin 2015, 19:26 Mer 24 Juin 2015, 19:26 | |
| Pour les CPGE et équivalent
Pour tout t réel , sin(t)=sum_{n=0}^{+oo} (-1)^n t^{2n+1}/(2n+1)!
sin(5x)=2sin(3x)sin(4x)
<==>
sum_{n=0}^{+oo} (-1)^n (5x)^{2n+1}/(2n+1)!
=2sum_{n=0}^{+oo} (-1)^n (3x)^{2n+1}/(2n+1)! sum_{n=0}^{+oo} (-1)^n (4x)^{2n+1}/(2n+1)!
produit de Cauchy ..... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: belle équation trigo Sujet: Re: belle équation trigo  | |
| |
|
  | |
| | belle équation trigo |  |
|
