|
| | Equation fonctionnelle: |  |
| | | Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Equation fonctionnelle: Sujet: Equation fonctionnelle:  Sam 20 Juin 2015, 13:04 Sam 20 Juin 2015, 13:04 | |
| Soit 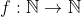 une fonction tel que >0) et :f(m^2+n^2)=f(m)^2+f(n)^2) . Montrez que :f(n)=n) . Bonne chance. | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Equation fonctionnelle: Sujet: Re: Equation fonctionnelle:  Dim 21 Juin 2015, 17:01 Dim 21 Juin 2015, 17:01 | |
| il m'arrivait souvent de trifouiller dans l’équation : m²+n²=u²+t² , dans mon souvenir ce quadruplet (p,p-2s, (p+3s)\2 , (p-5s)\2) p et s dans N est une solution ,de la on peut finir le problème par une récurrence forte sur p , en effet si on choisit s=p(mod 2) on a s=< 1 car les restes modulos 2 sont soit 0 ou 1 , donc pour p > 5 on p >5s et p+3s\2 =< p+3 \2 < p , donc par récurrence forte il vient f(p)²=p² => f(p)=p , pour p=< 5 il est facile de calculer les valeurs de f en ces points partant de f(1)=1 , qui donne f(2)=2 , et f(0)=0.... | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Equation fonctionnelle: Sujet: Re: Equation fonctionnelle:  Dim 21 Juin 2015, 21:57 Dim 21 Juin 2015, 21:57 | |
| - Oty a écrit:
- il m'arrivait souvent de trifouiller dans l’équation : m²+n²=u²+t² , dans mon souvenir ce quadruplet (p,p-2s, (p+3s)\2 , (p-5s)\2) p et s dans N est une solution ,de la on peut finir le problème par une récurrence forte sur p , en effet si on choisit s=p(mod 2) on a s=< 1 car les restes modulos 2 sont soit 0 ou 1 , donc pour p > 5 on p >5s et p+3s\2 =< p+3 \2 < p , donc par récurrence forte il vient f(p)²=p² => f(p)=p , pour p=< 5 il est facile de calculer les valeurs de f en ces points partant de f(1)=1 , qui donne f(2)=2 , et f(0)=0....
Oui, l'idée de départ est bonne! Cependant, le quadruplet n'est pas une solution à l'équation, et de plus le troisième et le quatrième membre du quadruplet peuvent ne pas être des entiers. L'inégalité que tu montres pour pouvoir utiliser l'hypothèse de récurrence n'est pas vraie aussi (mais là ce n'est pas un problème car tu peux bien évidemment appliquer la récurrence pour le calcul de l'image du plus grand élément du quadruplet) ! | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Equation fonctionnelle: Sujet: Re: Equation fonctionnelle:  Lun 22 Juin 2015, 04:02 Lun 22 Juin 2015, 04:02 | |
| (p,(p-5s)\2 , p-2s , (p+3s)\2 ) voici un quadriplet solution maintenant le problème est résolue avec la même démarche , en faite nmo je n'essaye pas de trouver la solution general de l'equation juste un quadriplet qui marche , quand je prend s=p(mod2) tout les membres du quadruplet sont parfaitement définie et sont tel que peut finir le probleme par reccurence , c'etait juste approche pour resoudre le probleme et non une solution bien rédigé je pense que c'est ce qui t'a un peu ambiguë Merci | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Equation fonctionnelle: Sujet: Re: Equation fonctionnelle:  Lun 22 Juin 2015, 13:43 Lun 22 Juin 2015, 13:43 | |
| P(m,n) : f(m²+n²)=f(m)²+f(n)²
P(0,0) : f(0)=2f(0)² ==> f(0)=0 car f(0) entier
P(1,0) : f(1)=f(1)² et f(1)>0 ==> f(1)=1
P(m,0): f(m²)=f(m)²
P(m,1): f(m²+1)=f(m)²+1
P(m,m): f(2m²)=2f(m)²
==> f(2)=2 , f(4)=4, f(5)=f(2²+1)=5
f(25)=f(9+16)=f(3)²+f(4)²=25 ==> f(3)=3
de la même façon on montre que f(6)=6, ...., f(12)=12
Par récurrence :
Supposons que pour tout k =<2n , f(k)=k pour un certain n>=6
(2n + 1)² + (n − 2)² = (2n − 1)² + (n + 2)²
==> f(2n + 1)² + f(n − 2)² = f(2n − 1)² + f(n + 2)²
mais n − 2=<2n , 2n − 1=<2n et n + 2=<2n ==> f(2n+1)=2n+1
(2n + 2)² + (n − 4)² = (2n − 2)² + (n + 4)²
==> f(2n + 2)² + f(n − 4)² =f(2n − 2)² + f(n + 4)²
mais n − 4=<2n , 2n − 2=<2n et n + 4=<2n ==> f(2n+2)=2n+2 | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Equation fonctionnelle: Sujet: Re: Equation fonctionnelle:  Lun 22 Juin 2015, 18:01 Lun 22 Juin 2015, 18:01 | |
| jolie MrAttioui Bravo  | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Equation fonctionnelle: Sujet: Re: Equation fonctionnelle:  | |
| |
|   | | | | Equation fonctionnelle: |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
