| | Problème de Septembre 2007 |  |
|
+3radouane_BNE selfrespect abdelbaki.attioui 7 participants |
| Auteur | Message |
|---|
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Problème de Septembre 2007 Sujet: Problème de Septembre 2007  Sam 01 Sep 2007, 14:19 Sam 01 Sep 2007, 14:19 | |
| Soit d(n) le nombre des chiffres de n écrit en représentation décimale.
Evaluer la somme : (somme de n=1 à +00 ) 1/d(n)! | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Sam 01 Sep 2007, 14:20 Sam 01 Sep 2007, 14:20 | |
| Salut,
Pour participer prière de :
1) Poster votre réponse par E-MAIL
abdelbaki.attioui@menara.ma
2) Envoyer ici le message "Solution postée"
Merci | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Sam 01 Sep 2007, 16:55 Sam 01 Sep 2007, 16:55 | |
| Salam ;
solution postée.
on pose:
tt d'abord on remarque que d(n)=E(log(n)+1)
preuve :facil a mdemontrer on remarquant seulemnt que 10^{E(log(n))+1}>n=10^{E(log'n)}>=10^{E(log(n))}.
♦maintenant retournons a Sn:
on remarque que:
tel que pour k fixé:
alors
remarquant que exp(x)=sum{k=0^+00}x^k/k!
on deduit :
sauf erreure de calculs ma part.
a+
Les formules n'apparaissent pas car ecrites en LATEX mais c'est juste
Champion | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Lun 03 Sep 2007, 13:45 Lun 03 Sep 2007, 13:45 | |
| Salam ;
solution postée.
sigma(k=->n)1/d(n)!=9*1/1!+90*1/2!+900*1/3!+.....=9/10*(10^1/1!+10^2/2!+...+10^n*1/n!)
d'où lim(n->+00)sigma(k=1->n)(1/d(n)!)=10/9(exp(10-1)
NOTA BENNE: lim(n->+00)(1+a/1!+a^2/2!+....+a^n/n!)=exp(a).
Champion | |
|
  | |
Raa23
champion de la semaine

 Nombre de messages : 179 Nombre de messages : 179
Age : 39
Date d'inscription : 02/04/2007
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Mer 05 Sep 2007, 17:16 Mer 05 Sep 2007, 17:16 | |
| Solution Postée
(Rebonjour à tous!!)
0..9
10..99
100..999
10*1 + 100*1/2! + 10^3*1/3! ..
Sn=sum( 10^n/n! ,n=1..inf )
Sn=e^10
Raa23
| |
|
  | |
aliaz
Débutant
Nombre de messages : 6
Date d'inscription : 29/01/2006
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Lun 10 Sep 2007, 14:47 Lun 10 Sep 2007, 14:47 | |
| salut a tous
solution postée
salut a tous
voila ce que je propose
on a d(n) peut prendre toytes les valeurs entieres >0
de plus pour tout k de N* il existe exactement 10^k-10^(k-1) entiers
dont le nombre de chiffres est k
don notre somme S vaut S=(somme de n=1 à +00 ) 1/d(n)!
=(somme de n=1 à +00 ) (10^k-10^(k-1))/k!
et en utilisant la formule exp(x)=(somme de n=1 à +00 )(x^k/k!)
on obtient S=9(e^10-1)/10 (sauf erreur)
voila
aliaz
Champion | |
|
  | |
callo
Expert sup

 Nombre de messages : 1481 Nombre de messages : 1481
Age : 34
Localisation : paris
Date d'inscription : 03/03/2007
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Mer 12 Sep 2007, 16:36 Mer 12 Sep 2007, 16:36 | |
| salut,
solution postée.
bonjour,
voici la solution du pb du mois de septembre ci-joint.
merci
Le fichier envoyé n'est pas accessible :
probléme de septembre.docx | |
|
  | |
massmoss
Féru

 Nombre de messages : 47 Nombre de messages : 47
Age : 47
Date d'inscription : 24/08/2007
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  Sam 15 Sep 2007, 21:26 Sam 15 Sep 2007, 21:26 | |
| salm a tous les participantssolution postée. BSR voila la reponse du probleme de septembre 2007; j'espère qu'il sera correcte
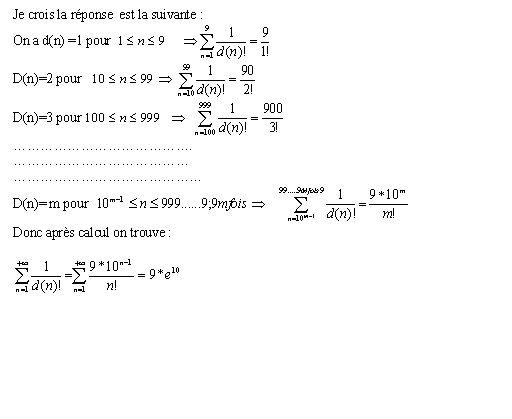 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Problème de Septembre 2007 Sujet: Re: Problème de Septembre 2007  | |
| |
|
  | |
| | Problème de Septembre 2007 |  |
|
