Aide urgente SVP

(quelque soit n de N*)(y a o moins (pn,qn)£N*)
tel que (2+V3)^n=p_n+(q_n)V3
3(q_n)²=(p_n)²-1

démontez par récurrence
et Mircé



P.S le "n" à coté de p et q est un indice et n'oubliez pas que c'est un système

J y réfléchi encore à ce satané exo.

une réponse walou ze3ma????????????????

On a cet excercice dans le manuel... Moi non plus je n'ai pas réussi à le faire... J'ai demandé à mon prof de maths comment le résoudre et il a dit que c'était trèès facile Et demain j'ai un examen de maths et il a dit qu'il sera facile...(Je sais bien que pour lui le facile c'est le difficile xD) Si quelqu'un pouvait bien le faire ça serait sympa

cet koi un systeme en arabe?

ça veut dire : Nidma ^^

huntersoul a écrit:

(quelque soit n de N*)(y a o moins (pn,qn)£N*)
tel que (2+V3)^n=p_n+(q_n)V3
3(q_n)²=(p_n)²-1
démontez par récurrence
et Mircé
P.S le "n" à coté de p et q est un indice et n'oubliez pas que c'est un système

Je vous donne des INDICATIONS !!!
Utiliser la formule du Binôme de NEWTON et montrer que l'on peut écrire :
(2+rac3)^n= An +Bn.rac3 avec An et Bn dans N*
Etablir des relations entre A(n+1), B(n+1) et An , Bn .
Vérifier par la suite que :
(2-rac3)^n=An-Bn.rac3
Enfin , évaluer (2+rac3)^n . (2-rac3)^n de deux manières différentes pour trouver :
(4-3)^n = 1 = (An)^2 - 3.(Bn)^2
Votre p_n c'est An
et q_n c'est Bn .

A+ LHASSANE

slt tt lemonde!
pour la méthode qu'a suggéré M.LHASSANE (le binome de newton), je crois qu'on ne l'a pâs encore étudier (jusqu'à la leçon du dénombrement).
voila comment j'ai pu démontrer cet exo, et a vous de voir!
j'ai utulisé effectivement la récurrence et ça a donné résultat!

on nous demande de prouver que :
(quelque soit n de IN*)(Il existe (pn,qn)£ IN*²):
(2+V3)^n=p_n+(q_n)V3 et
3(q_n)²=(p_n)²-1

• pour n=1 on a :
  

(2+V3)^n=2+1*V3 et on a : 3*1²=2²-1
donc effectivement, pour n=1, Il existe (pn,qn)£ IN*² (pn=2 et qn=1) tel que laproposition au dessus est réalisée.

• soit n un entier naturel non nul.
  

supposons que la proposition est réalisée jusqu'a n, et démontrons qu'elle est vraie pour (n+1).
on a :
(2+V3)^(n+1)=(2+V3)*(2+V3)^n
et d'après la supposition de la récurrence:
(2+V3)^n=p_n+(q_n)V3
donc:
(2+V3)^(n+1)=(2+V3)*(p_n+(q_n)V3)
=2p_n+2V3q_n+V3p_n+3q_n
(2+V3)^(n+1)= (2p_n+3q_n)+V3(p_n+2q_n)
et on a :
3(pn+2qn)²=3(p_n)²+12p_n*q_n+12(q_n)²
=4(p_n)²+12p_n*q_n+9(q_n)²+3(q_n)²-(p_n)²
=(2p_n+3q_n)²+ 3(q_n)²-(p_n)²
et d'après la supposition de récurrence : 3(q_n)²-(p_n)²= -1
donc 3(pn+2qn)²=(2p_n+3q_n)²-1
alors il existe p_(n+1)=2p_n+3q_n et q_(n+1)=p_n+2q_n de IN* tel que:
(2+V3)^(n+1)=p_(n+1)+(q_n+1)V3 et
3(q_n+1)²=(p_n+1)²-1.

• par conséquent, selon le principe de récurrence:
  

(quelque soit n de IN*)(Il existe (pn,qn)£ IN*²):
(2+V3)^n=p_n+(q_n)V3 et
3(q_n)²=(p_n)²-1

Oui , Rim !!!
C'est tout à fait JUSTE et de votre niveau !!!
BRAVO !!!
A+ LHASSANE

merci Mr Lhssane et rim pour votre aide

j'ai fais moi aussi quelque chose dont je suis pas sur
Pour la vérifivation c ok
mnt la méthode on suppose que la propostion est juste pour n=1
on a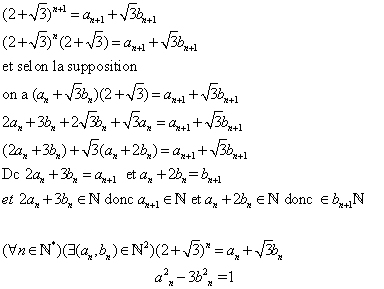

j'espère que c'est juste

merci bcq M.LHASSANE et huntersoul!