ex

f fonction tel que f(x)=(x-E(x))²
montrez que f mahdouda et que 1 dawroha

Alaoui.Omar a écrit:

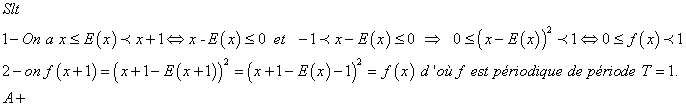BJR Omar !!!
On a toujours
E(x)<=x<E(x)+1 donc 0<=x-E(x)<1 !!!!!!
Ce que je ne comprends pas c'est :
Pourquoi Matheux-03 a considéré la fonction f
x-------> f(x) ={x-E(x)}^2
alors que l'on connait les mêmes conclusions pour la fonction g
x------->g(x)=x-E(x)
il ne restait plus qu'à composer g et la fonction t
x------->t(x)=x^2 pour avoir ce qu'il faut !!!!
A+ BOURBAKI

Sinon, la réponse à la 2eme question est fausse, ou plutôt incomplète:
Omar tu as montré que 1 est une période de la fonction, mais dire que f est périodique de période T signifie que le T en question est le plus petit réel strictement positif qui soit une période de la fonction.
Il fallait ajouter que f(T) = f(0) = 0, donc que T est forcément un entier, avant de conclure que la période de f est 1.

dala dawriya

No-Eni a écrit:

dala dawriya

bon jour adepte de la statue enrispa

hamzaaa a écrit:

Sinon, la réponse à la 2eme question est fausse, ou plutôt incomplète:
Omar tu as montré que 1 est une période de la fonction, mais dire que f est périodique de période T signifie que le T en question est le plus petit réel strictement positif qui soit une période de la fonction.
Il fallait ajouter que f(T) = f(0) = 0, donc que T est forcément un entier, avant de conclure que la période de f est 1.

Salut Hamza , Merci Pour la Remarque ...