galois2000
Féru
 Nombre de messages : 42 Nombre de messages : 42
Age : 35
Date d'inscription : 15/07/2008
 |  Sujet: nice result Sujet: nice result  Mer 23 Juil 2008, 18:53 Mer 23 Juil 2008, 18:53 | |
| soit: 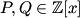 telle que pour n£Z on a: 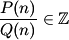 prouver que : 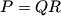 avec: 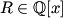 | |
|
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: nice result Sujet: Re: nice result  Mer 23 Juil 2008, 21:30 Mer 23 Juil 2008, 21:30 | |
| Utiluse les polynomes d'interpolation de lagrange ,
ps:est ce que tu as deja passé le sup ? | |
|
exodian95
Modérateur
 Nombre de messages : 246 Nombre de messages : 246
Age : 24
Date d'inscription : 27/06/2008
 |  Sujet: Re: nice result Sujet: Re: nice result  Mer 23 Juil 2008, 22:06 Mer 23 Juil 2008, 22:06 | |
| Salut selfrespect,
Je connais très bien les polynomes d'interpolation de lagrange, mais je vois mal leur utilisation ici.
Pourriez vous expliquer? | |
|
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: nice result Sujet: Re: nice result  Mer 23 Juil 2008, 22:16 Mer 23 Juil 2008, 22:16 | |
| - exodian95 a écrit:
- Salut selfrespect,
Je connais très bien les polynomes d'interpolation de lagrange, mais je vois mal leur utilisation ici.
Pourriez vous expliquer? Salut , avec plaisir : notons RQ=P ,m=deg(R) on a les reels R(1) ,R(2),....R(m) , sont des rationnels , soit T(x)=sum_{i=O,1..m} R(i).Li(x) avec Li(x)=Prod_{i=O.k-1,k+1...m}(x-i)/{prod(k-i), i#k} on a biensur T(i)=R(i) qq soit i de {o,1...,m} or le deg de R est m ( et aussi celui de T) donc on deduit que R et T sont proportionel , soit a tq :T=aR , pr x=1 on a T(1) et R(1) sont des rationnels alors a aussi , d'ou le resultats! puisque T est deja dans Q[X] (s,e) desoé latex ne marche po aujourd'hui ! A+ | |
|
exodian95
Modérateur
 Nombre de messages : 246 Nombre de messages : 246
Age : 24
Date d'inscription : 27/06/2008
 |  Sujet: Re: nice result Sujet: Re: nice result  Mer 23 Juil 2008, 22:25 Mer 23 Juil 2008, 22:25 | |
| Merci beaucoup selfrespect  | |
|
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: nice result Sujet: Re: nice result  Mar 19 Aoû 2008, 20:02 Mar 19 Aoû 2008, 20:02 | |
| autre solution.
la division euclidienne donne:P=QR+S avec deg(S(x))<deg(Q(x))=n.dans cette exprerssion on a a_n^n*R(x)£Z[X] avec Q(x)=a-n*x^n+....
Or puisque a_n^n*S(x)/Q(x)£Z pour tout n de IN alors S=0.
CQFD! | |
|
