| | Séries de logique |  |
|
+4ouths Koutaiba Perelman ADISON 8 participants |
| Auteur | Message |
|---|
ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Séries de logique Sujet: Séries de logique  Mar 23 Sep 2008, 21:48 Mar 23 Sep 2008, 21:48 | |
| Bonsoir les amis ...  | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 23 Sep 2008, 22:02 Mar 23 Sep 2008, 22:02 | |
| merci bcp pour la serie ADISON | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 23 Sep 2008, 22:03 Mar 23 Sep 2008, 22:03 | |
| je crois pour le permier exo il y a une faute ... | |
|
  | |
ouths
Féru

 Nombre de messages : 43 Nombre de messages : 43
Age : 34
Date d'inscription : 11/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 23 Sep 2008, 22:38 Mar 23 Sep 2008, 22:38 | |
| - Koutaiba a écrit:
- je crois pour le permier exo il y a une faute ...
.slt ; supposant que /l-l'/#0 ==> il existe k>0 tel que /l-l'/=k ==>/l-l'/=k>k/2 et k/2 >0 contradiction . donc l=l' | |
|
  | |
botmane
Expert grade1

 Nombre de messages : 411 Nombre de messages : 411
Age : 32
Localisation : surement chez moi
Date d'inscription : 03/04/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mer 24 Sep 2008, 01:10 Mer 24 Sep 2008, 01:10 | |
| - ouths a écrit:
- Koutaiba a écrit:
- je crois pour le permier exo il y a une faute ...
.slt ;
supposant que /l-l'/#0 ==> il existe k>0 tel que /l-l'/=k ==>/l-l'/=k>k/2
et k/2 >0 contradiction .
donc l=l' juste ! | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mer 24 Sep 2008, 16:59 Mer 24 Sep 2008, 16:59 | |
| pour la 2éme exo :
1-
x-x^2 = x(1-x)
et on sait que :
0=<x=<1
alors
x(1-x) >=0
d' autre part on a
4(1/4 - x + x^2) = 4 x^2 - 4x + 1 = (2x-1)^2 >=0
donc
0=<x-x^2=<1/4
2-a-
An.Bn = II xi * II (1-xi) = II (xi - xi^2 )
on sait que
0=<x-x^2=<1/4
alors
0=< II (xi - xi^2 ) =< II (1/4)
0=<II xi * II (1-xi) =< (1/4)^n
0=< An.Bn =< 1/(4^n) | |
|
  | |
yugayoub
Expert sup

 Nombre de messages : 842 Nombre de messages : 842
Age : 32
Localisation : Cimetiere famillial: la maison
Date d'inscription : 13/07/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Jeu 25 Sep 2008, 23:27 Jeu 25 Sep 2008, 23:27 | |
| | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 13:12 Mar 30 Sep 2008, 13:12 | |
| salut tt le monde pour l'exo N8: 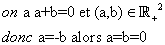  | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 13:26 Mar 30 Sep 2008, 13:26 | |
| salut les amis
pour l'exo N6
est-ce-qu'on va dire que V2 et V3 n'apprtient pas à Q .. alors leur somme et leur produit aussi n'apprtient pas à Q ??? | |
|
  | |
ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 16:14 Mar 30 Sep 2008, 16:14 | |
| - h99 a écrit:
- merci bcp pour la serie ADISON
de rien..  | |
|
  | |
ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 16:16 Mar 30 Sep 2008, 16:16 | |
| - yugayoub a écrit:
- merci bcp
de rien  ... mais il faut essayer de la résoudre ...  | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 16:34 Mar 30 Sep 2008, 16:34 | |
| j'ai resolu le 8eme exo!!!!!!!!!!!!!! | |
|
  | |
ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 16:36 Mar 30 Sep 2008, 16:36 | |
| - h99 a écrit:
- j'ai resolu le 8eme exo!!!!!!!!!!!!!!
C'est juste mon ami h99 ...  | |
|
  | |
ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Mar 30 Sep 2008, 16:38 Mar 30 Sep 2008, 16:38 | |
| - Koutaiba a écrit:
- salut les amis
pour l'exo N6
est-ce-qu'on va dire que V2 et V3 n'apprtient pas à Q .. alors leur somme et leur produit aussi n'apprtient pas à Q ??? en attendant de résoudre l'exercice 6 | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 13:55 Ven 03 Oct 2008, 13:55 | |
| - Koutaiba a écrit:
- salut les amis
pour l'exo N6
est-ce-qu'on va dire que V2 et V3 n'apprtient pas à Q .. alors leur somme et leur produit aussi n'apprtient pas à Q ??? SVP les amis .. comment faire pour l'exo N6 ??? | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 20:37 Ven 03 Oct 2008, 20:37 | |
| N'y a-t-il personne ici ?? | |
|
  | |
Chessmaster
Maître
 Nombre de messages : 163 Nombre de messages : 163
Age : 32
Date d'inscription : 02/10/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 20:53 Ven 03 Oct 2008, 20:53 | |
| ça serait de supposer directement : V6-V2-V3=p/q
Vouloir démontrer l'irrationalité de V6,V2 et V3 chacune tout seule sera très long à faire. | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 21:13 Ven 03 Oct 2008, 21:13 | |
| Pourrais-tu mieux expliquer ??? | |
|
  | |
Chessmaster
Maître
 Nombre de messages : 163 Nombre de messages : 163
Age : 32
Date d'inscription : 02/10/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 21:44 Ven 03 Oct 2008, 21:44 | |
| on nous demande de démontrer que V6-V2-V3 est irrationnel donc on fait une démonstration par l'absurde en supposant qu'il est rationnel, et tout nombre rationnel s'écrit sous la forme p/q avec p et q premiers entre eux, sinon je ne sais pas comment continuer :p | |
|
  | |
spiderccam
Expert sup

 Nombre de messages : 584 Nombre de messages : 584
Age : 33
Date d'inscription : 27/10/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 22:04 Ven 03 Oct 2008, 22:04 | |
| tres bonne serie elle semble contenir un bon nombres d'astuces | |
|
  | |
Chessmaster
Maître
 Nombre de messages : 163 Nombre de messages : 163
Age : 32
Date d'inscription : 02/10/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 22:43 Ven 03 Oct 2008, 22:43 | |
| sinon je pense qu'on doit démontrer que chacun des nombres V6,V2 et V3 sont irrationnels, car en utilisant V6-V2-V3=p/q on bloque. | |
|
  | |
spiderccam
Expert sup

 Nombre de messages : 584 Nombre de messages : 584
Age : 33
Date d'inscription : 27/10/2007
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 22:54 Ven 03 Oct 2008, 22:54 | |
| utilise le conjuger mourafike | |
|
  | |
Chessmaster
Maître
 Nombre de messages : 163 Nombre de messages : 163
Age : 32
Date d'inscription : 02/10/2008
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  Ven 03 Oct 2008, 23:09 Ven 03 Oct 2008, 23:09 | |
| 1-2V6=p/q(V6+V2+V3)
la suite? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Séries de logique Sujet: Re: Séries de logique  | |
| |
|
  | |
| | Séries de logique |  |
|
