| | problème N°78 de la semaine (23/04/2007-29/04/2007) |  |
|
+14Bison_Fûté khamaths radouane_BNE R.kira stof065 aannoouuaarr Alaoui.Omar abdelbaki.attioui elhor_abdelali im@ne saiif3301 coucou rockabdel samir 18 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: problème N°78 de la semaine (23/04/2007-29/04/2007)  Lun 23 Avr 2007, 17:59 Lun 23 Avr 2007, 17:59 | |
|
_________________
وتوكل على الحي الذي لا يموت وسبح بحمده
| |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Lun 23 Avr 2007, 18:02 Lun 23 Avr 2007, 18:02 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci
_________________
وتوكل على الحي الذي لا يموت وسبح بحمده
| |
|
  | |
rockabdel
Maître
Nombre de messages : 264
Date d'inscription : 15/09/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Lun 23 Avr 2007, 19:21 Lun 23 Avr 2007, 19:21 | |
| Envoyée
voici la solution de rockabdel
Salut samir ,
X²+y²+z²+t²-xy-xz-xt=0 <==> (1/2x-y)²+(1/2x-z)²+(1/2x-t)²+1/4x²=0
A+b+c+d=0 et a, b, c et d supérieurs a 0 <==> a=0 et b=0 et c=0 et d=0
D’où S={(0,0,0,0)} | |
|
  | |
coucou
Maître

 Nombre de messages : 180 Nombre de messages : 180
Age : 33
Date d'inscription : 08/04/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Lun 23 Avr 2007, 21:40 Lun 23 Avr 2007, 21:40 | |
| Salut :
Solution postée
voici la solution de coucou
Salut :
l'équation vaut à : (x/2-y)² +(x/2-z)²+(x/2-t)²+ x²/4 =0
x=0 ; y=0 ; z=0 ; t=0 | |
|
  | |
saiif3301
Expert grade2
 Nombre de messages : 378 Nombre de messages : 378
Age : 33
Localisation : benslimane
Date d'inscription : 07/05/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Lun 23 Avr 2007, 21:50 Lun 23 Avr 2007, 21:50 | |
| solutions postèe
voici la solution de saiif3301
voila ma solution
x²+y²+z²+t²-xy-xz-xt=(1/2*x-y)²+(1/2*x-t)²+(1/2*x-z)²+1/4*x²=0 donc
x²=0 et
x=2y et x=2z et x=2t donc la seul solution sè x=y=z=t=0 de
saiif3301 | |
|
  | |
im@ne
Maître

 Nombre de messages : 271 Nombre de messages : 271
Age : 33
Localisation : à la mizo {lma9bara l3a2ilia}
Date d'inscription : 08/04/2007
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Lun 23 Avr 2007, 21:56 Lun 23 Avr 2007, 21:56 | |
| solution postéé voici la solution d'imanex²+y²+z²+t²-xy-xz-xt =0
x²=1/4x²+1/4x²+1/4x²+1/4x²
1/4x²-xy+y²+1/4x²-xz+y²+1/4x²-xz+z²+1/4x²-xt+t²
=1/(2x-y)²+1/(2x-z)²+(1/2x-t)²+1/4x²
et puiske un nombre caré >ou egale 0 donc 1/(2xy)²=0
et c o6 pr les otres carrés et puisque
1/(2x-y)²+1/(2x-z)²+(1/2x-t)²=0
donc 1/4x²=0
résultat:
1/(2x-y)²+1/(2x-z)²+(1/2x-t)²+1/4x²=x²+y²+z²+t²-xy-xz-xt=0
x²+y²+z²+t²-xy-xz-xt=0
jéspère ke c correcte ,
merci à stof065 .  | |
|
  | |
elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 61
Localisation : Maroc.
Date d'inscription : 24/01/2006
 | |
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Mar 24 Avr 2007, 09:35 Mar 24 Avr 2007, 09:35 | |
| Bonjour solution postée voici la solution d'abdelbaki.attiouiBonjour, même chose que
a²+b²+c²+d²+e²=>a(b+c+d+e)
x²+y²+z²+t²-xy-xz-xt=0
<==>(y-x/2)²+(z-x/2)²+(t-x/2)²+x²/4=0
<==>x=y=z=t=0
A+
_________________
وقل ربي زد ني علما
| |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 33
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Mar 24 Avr 2007, 11:20 Mar 24 Avr 2007, 11:20 | |
| Bonjour Solution postée 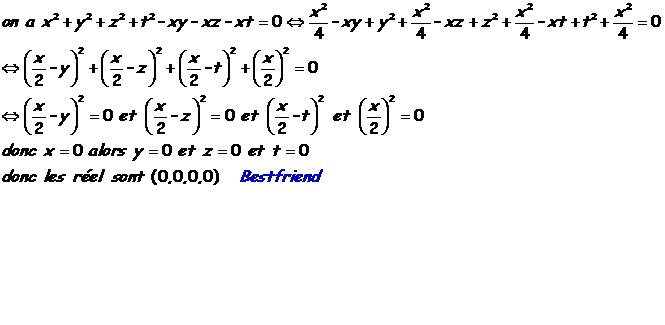 | |
|
  | |
aannoouuaarr
Maître
 Nombre de messages : 154 Nombre de messages : 154
Age : 35
Localisation : meknes
Date d'inscription : 14/11/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Mar 24 Avr 2007, 19:04 Mar 24 Avr 2007, 19:04 | |
| solution postée
voici la solution d'anouar
x=0 <==> y²+z²+t²=0 <=> x=y=z=t=0
si x#0 alors x²/3+y²>x²/4+y²>=xy de la meme facon x²/3+z²>xz et
x²/3+t²>xy
en sommant==> x²+y²+z²+t²>xy+xz+xt cad l'equation n a pas de solution
pr x#0
S={(0,0,0,0)} | |
|
  | |
stof065
Expert sup

 Nombre de messages : 540 Nombre de messages : 540
Age : 33
Date d'inscription : 01/02/2007
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Mar 24 Avr 2007, 19:07 Mar 24 Avr 2007, 19:07 | |
| solution postée
voici la solution de stof
on a
x²+y²+z²+t²-xy-xz-xt=0
((1/2)x-y)²+ ((1/2)x-z)²+ ((1/2)x-t)²+1/4x²=0
On a ((1/2)x-y)²+ ((1/2)x-z)²+ ((1/2)x-t)²+1/4x²>=0
Cela implique que
((½)x-y)²=0 et ((1/2)x-z)²=0et((½)x-y)²=0et 1/4x²=0
(½)x-y=0 et (1/2)x-z=0et(½)x-y=0et x=0
De cela on déduit que les seuls nombres qui réalisent cette relation
Et x=y=z=t=0
Stof065
A+ | |
|
  | |
R.kira
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 34
Date d'inscription : 17/04/2007
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Mar 24 Avr 2007, 19:32 Mar 24 Avr 2007, 19:32 | |
| solution postée
voici la reponse de kira
On a x²+y²+z²+t²-xy-xz-xt=0 equiv.à
1/4x²-xy+y²+1/4x²-xz+z²+1/4x²-xt+t²+1/4x²=0
Equiv.à (1/2x+y)²+(1/2x+z)²+(1/2x+t)²+1/4x²=0
Equiv.à x=0 et y=0 et z=0 et t=0
D’où les valeurs sont : x=0 et y=0 et z=0 et t=0
r.kira (reda bouchry) | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Mar 24 Avr 2007, 21:22 Mar 24 Avr 2007, 21:22 | |
| salut tout le monde.
soution postée
solution non trouvée parmis mes mails (administration)
(N'oublies pas d'ecrire ton nom d'utilisateur dans la réponse envoyée) | |
|
  | |
khamaths
Maître
Nombre de messages : 98
Date d'inscription : 17/03/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Jeu 26 Avr 2007, 15:55 Jeu 26 Avr 2007, 15:55 | |
| Bonjour
Solution postée
voici la solution de khamaths
Bonjour Samir
on a: x² + y² + z² + t² = x ( y + z + t ) (1)
D'après l'inégalitée de Cauchy-schwarz on a:
(x + y + z + t )² <= 4 ( x² + y² + z ²+ t ²)
<===> (x + y + z + t )² <= 4x (y +z + t) (d'après (1))
<===>[x - (y + z + t) ]² <= 0
<===>x = y + z + t
(1) <==> y² + z² + t² = 0
<===> y = z = t = 0
conclusion: la seule solution est (0;0;0;0) | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 64
Date d'inscription : 11/02/2007
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Ven 27 Avr 2007, 12:10 Ven 27 Avr 2007, 12:10 | |
| Bonjour Mr SAMIR !!!
Solution au Pb 78 postée ce jour.
voici la solution de BOURBAKI
L’équation que vous proposez cette semaine est du type :
F(x,y,z,t) = 0
Avec F(x,y,z,t) = x^2+y^2+z^2+t^2-xy-xz-xt dont l’ensemble des solutions dans IR sera noté S .
La forme quadratique F est décomposable en somme de 4 carrés comme suit :
F(x,y,z,t) = [y-(x/2)]^2 + [z-(x/2)]^2 + [t-(x/2)]^2 + [(x/2)]^2
Par suite, la relation F(x,y,z,t) = 0 exige la nullité de chacun de ces 4 carrés et partant ,
on devrait avoir y = z = t = x/2 puis x = 0
En conclusion, on a une seule solution et S = {(0,0,0,0)}
UNE AUTRE SOLUTION : on pourrait aussi essayer d’exprimer explicitement x en fonction de y,z et t .
On sera amené à étudier un trinôme du second degré en x à coefficients dépendants de y, z et t
x^2+B.x+C=0
avec B= - (y+z+t) et C = y^2+z^2+t^2
Le discriminant de ce trinôme est Delta = 2.[yz+yt+zt] – 3.[ y^2+z^2+t^2] utilisant l’inégalité classique
2.a.b <=[a^2+b^2] pour tout a, b dans IR alors il en résulte que
Delta <= - [y^2+z^2+t^2] <=0
On s’interesse aux solutions réelles donc Delta >=0 et de là Delta =0 ceci exige
y = z = t = 0 et x = 0 et on retrouve la conclusion de la méthode précédente. | |
|
  | |
Kendor
Féru
Nombre de messages : 64
Localisation : Malakoff (92240)
Date d'inscription : 13/12/2005
 |  Sujet: Solution au problème de la semaine n°78 par Kendor Sujet: Solution au problème de la semaine n°78 par Kendor  Ven 27 Avr 2007, 16:44 Ven 27 Avr 2007, 16:44 | |
| Bonjour!
Solution postée.
voici la solution de Kendor
On a x²+y²+z²+t²-xy-xz-xt=0
Donc x²+(y-x/2)²-x²/4+(z-x/2)²- x²/4+(t-x/2)²- x²/4=0
Donc x²/4+(y-x/2)²+(z-x/2)²+(t-x/2)²=0
D’où x/2=y=z=t et x=0
Donc x=y=z=t=0.
A+
Ciao!
Kendor. | |
|
  | |
badr
Expert sup

 Nombre de messages : 1408 Nombre de messages : 1408
Age : 34
Localisation : RIFLAND
Date d'inscription : 10/09/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Ven 27 Avr 2007, 20:29 Ven 27 Avr 2007, 20:29 | |
| solution postee
voici la solution de badr
salut samir
x²+y²+z²+t²-xy-xz-xt=0
on multipe le polynome avec4
4x²+4y²+4z²+4t²-4xy-4xz-4xt=0
on a les identitee remarquables
x²-4xy+4y²+x²-4xz+4z²+x²-4xt+4t²+x²=0
(x-2y)²+(x-2z)²+(x-2t)²+x²=0
on cluclant de la somme de quatre nombre positive ou egale a
0
que (x-2y)²=0
(x-2z)²=0
(x-2t)²=0
x²=0
que (x-2y)=0
(x-2z)=0
(x-2t)=0
x=0
x=2y
x=2z
x=2t
x=0
donc x=y=z=t=0 | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 33
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Dim 29 Avr 2007, 17:04 Dim 29 Avr 2007, 17:04 | |
| Salut
solution postée
voici la réponse de codex
x²+y²+z²+t²-xy-xz-xt=0
<=>4x²+4y²+4z²+4t²-4xz-4xt-4xy=0
<=>(x²-4xy+4y²)+(x²-4xz+4z²)+(x²-4xt+4t²)+x²=0
<=>(x-2y)²+(x-2z)²+(x-2t)²+x²=0
donc x=0 y=0 z=0 t=0 | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 33
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  Dim 29 Avr 2007, 17:33 Dim 29 Avr 2007, 17:33 | |
| salut Mr Samir
solution postée
voici la solution de conana
On : (x² +y²) + (x²+z²)+(t² + x²) ≥ xy + xz +xt
Donc : 2x² + (x² +y² +z² +t² - xy - xz – xt ) ≥ 0
Alors : 2x² ≥ 0
Càd l'equation [x² +y² +z² +t² - xy - xz – xt = 0 ] est vrai pour tous x,y,z,t de R !!! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007) Sujet: Re: problème N°78 de la semaine (23/04/2007-29/04/2007)  | |
| |
|
  | |
| | problème N°78 de la semaine (23/04/2007-29/04/2007) |  |
|
