| | problème N°128 de la semaine (07/04/2008-13/04/2008) |  |
|
+4iverson_h3 memath rachid18 samir 8 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: problème N°128 de la semaine (07/04/2008-13/04/2008)  Lun 07 Avr 2008, 21:17 Lun 07 Avr 2008, 21:17 | |
|
_________________
وتوكل على الحي الذي لا يموت وسبح بحمده
| |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Lun 07 Avr 2008, 21:19 Lun 07 Avr 2008, 21:19 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci
_________________
وتوكل على الحي الذي لا يموت وسبح بحمده
| |
|
  | |
rachid18
Expert grade2

 Nombre de messages : 369 Nombre de messages : 369
Age : 32
Date d'inscription : 23/03/2008
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Lun 07 Avr 2008, 22:23 Lun 07 Avr 2008, 22:23 | |
| solution postée
voici la solution de rachid18
En multipliant par (x+1)(y+1)(z+1) on trouve qu’on doit prouver que :
x²+y²+z²+x²y+y²x+z²y >= x+y+z+3
On a : x²y+y²x+z²y >=3 (inégalité de moyenne avec xyz=1),
Alors prouvons que : x²+y²+z² >=x+y+z,
On a x²+1>=2x
y²+1>=2y
z²+1>=2z
En sommant on trouve que : x²+y²+z² >= 2x+2y+2z-3
Et puis ce que x+y+z >=3 (inégalité de moyenne avec xyz=1)
Alors 2x+2y+2z-3 >=x+y+z
Alors x²+y²+z² >=x+y+z.
Alors l’inégalité voulue est prouvée. | |
|
  | |
Invité
Invité
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Mar 08 Avr 2008, 11:12 Mar 08 Avr 2008, 11:12 | |
| Solution postée
voici la solution de neutrino
L'inégalité équivaut à:
x²+y²+z²-x-y-z+x²z+y²x+z²y-3>=0
ce qui est trivial en effet ona:
x²+y²+z² >= (x+y+z)²/3 = (x+y+z)*(x+y+z)/3 >= (x+y+z) ( Cauchy+AM-GM)
et x²z+y²x+z²y>=3xyz=3 (AM-GM)
A+ |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Mar 08 Avr 2008, 11:36 Mar 08 Avr 2008, 11:36 | |
| postée voici la solution de memathon a :  (1) par AM-GM :  donc x+y+z>=3 ce qui montre que 1() est vraie  | |
|
  | |
iverson_h3
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 32
Date d'inscription : 08/09/2007
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Mar 08 Avr 2008, 13:01 Mar 08 Avr 2008, 13:01 | |
| solution postée par e-mail 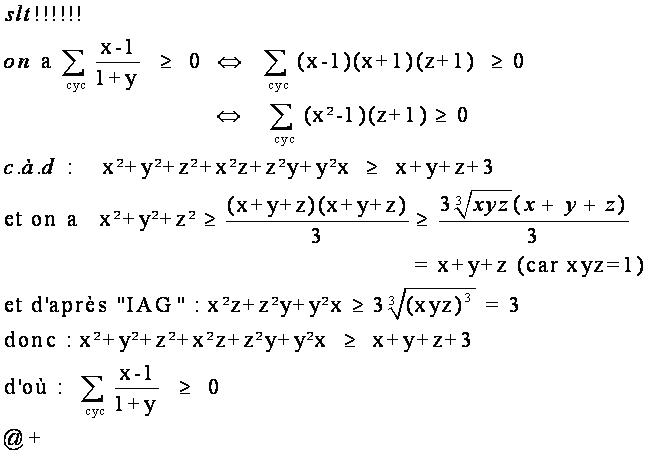 | |
|
  | |
joystar1
Maître
 Nombre de messages : 148 Nombre de messages : 148
Age : 34
Date d'inscription : 17/03/2007
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Dim 13 Avr 2008, 13:05 Dim 13 Avr 2008, 13:05 | |
| solution postée
on note S le terme gauche.
S>=0 =>x²+y²+z²+(x²z+z²y+y²x-3)-(x+y+z)>=0
=>x²+y²+z²-(x+y+z)>=0(AM-GM et xyz=1)
=>(x+y+z)((x+y+z)/3-1)>=0 (moyenne quadratique et arithmetique)
=>(x+y+z)>=0 (am-gm et xyz=1)
ce qui est tjs vrais(xyz>0) | |
|
  | |
fezzibasma
Maître

 Nombre de messages : 193 Nombre de messages : 193
Age : 33
Date d'inscription : 24/02/2008
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Dim 13 Avr 2008, 14:05 Dim 13 Avr 2008, 14:05 | |
| c'est bon  postée voici la solution de fezzibasma( x-1)/(1+y)= (x-1)/(xyz+y) =x/(xyz+y)-1/(xyz+y)
la mm chose ca donne : pr les autres
(y-1)/(1+z)=y/(xyz+z)-1/(xyz+z)
(z-1)/(1+x)=z/(xyz+x)-1/(xyz+x)
puisque 1>0 et xyz>0 donc x>xyz>0
donc x/(xyz+y)> 1/(xyz+y) (xyz)>0
et y/(xyz+z)> 1/(xyz+z)
et z/(xyz+x)> 1/(xyz+x)
avec la somme en bleu ca donne le resultat demandé | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Dim 13 Avr 2008, 22:15 Dim 13 Avr 2008, 22:15 | |
| Bonjour
Solution postée
voici la solution d'abdelbaki.attiouiBonjour
L'inégalité <==> (x²-1)(1+z)+(y²-1)(1+x)+(z²-1)(1+y) >=0
<==> x²+y²+z²-x-y-z+x²z+xy²+yz²>=3
Mais, I.A.G donne x²+y²+z²>=3 (xyz)^(2/3)=3 et
x²z+x²z+xy²>=3(x^5y²z²)^(1/3)=3x
xy²+xy²+yz²>=3(x²y^5z²)^(1/3)=3y
x²z+yz²+yz²>=3(x²y²z^5)^(1/3)=3z
on obtient, en faisant la somme que x²z+xy²+yz² >= x+y+z d'où le résultat.
A+
_________________
وقل ربي زد ني علما
| |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 33
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  Sam 26 Avr 2008, 00:11 Sam 26 Avr 2008, 00:11 | |
| - memath a écrit:
- postée
voici la solution de memath
on a :
 (1) (1)
par AM-GM : 
donc x+y+z>=3 ce qui montre que 1() est vraie  ce n'est pas tjrs valable la premiére inégo , car méme si 1/(1+y)>=1/(1+y+x+t) ca ne signifit pas que (x-1)/(y+1)>=(x-1)/(1+x+y+z) ,(au cas ou x-1 =< 0) et si c'est vrai malgré cela , alors il faut le prouver  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008) Sujet: Re: problème N°128 de la semaine (07/04/2008-13/04/2008)  | |
| |
|
  | |
| | problème N°128 de la semaine (07/04/2008-13/04/2008) |  |
|
