quote="h-o-u-s-s-a-m"]salut
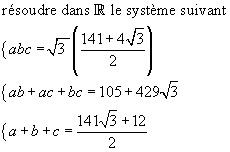
[/quote]
Salut !!
J'ai comme l'impression de reconnaitre des fonctions symétriques de racines !!!
Je crois que a , b et c sont solutions de l'équation du troisième degré :
(X-a).(X-b).(X-c)=0
Il n'y a qu'à développer et remplacer abc , ab+bc+ac et a+b+c par leurs valeurs et enfin résoudre l'équation du troisième degré par la méthode de CARDAN par exemple .
LHASSANEPS: Rédouane ! Tu es arrivé plus tôt que moi ce coup-ci !!!!!
