- issam erriahi a écrit:

Remarquons que
=4cos^3(x)-3cos(x))
Si nous arrivons à démontrer que
)
, la démonstration sera achevée. Nous avons :
=16cos^6(x)-24cos^4(x)+9cos^2(x))
Et donc :
=16cos^6(\frac{\pi%20}{9})-24cos^4(\frac{\pi%20}{9})+9cos^2(\frac{\pi%20}{9}))
Posons par absurde
=\frac{p}{q})
avec p et q deux entiers premiers entre eux. Nous avons alors :
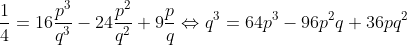
De ce fait, p divise q et puisque p et premier avec q, alors p=1,
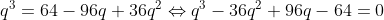
. Cette équation admet trois solutions non-entières et cela est aisément prouvable par TVI. Ce qui est absurde. Et donc
)
est irrationnel. Nous avons :
=\frac{1}{tan^2(\frac{\pi%20}{9})}=\frac{1}{\frac{1}{cos^2(\frac{\pi%20}{9})}-1})
et donc
)
est irrationnel, et donc :
)
est irrationnel.
Sauf erreur.
Au plaisir !
