issam erriahi
Expert sup
 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 | | Sujet: prove that Sam 02 Jan 2010, 18:15 | |
| | |
|
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: prove that Sam 02 Jan 2010, 18:23 | |
| x=y=z=0....
Il manque quelque chose .. | |
|
MohE
Expert grade2
Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
| | Sujet: Re: prove that Sam 09 Jan 2010, 18:57 | |
| Bonsoire!
Il manque le fait que x,y,z sont des réels tels xyz=1, c'est l'IMO 2008 qui était assez facile! | |
|
{}{}=l'infini
Expert sup
Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
| | Sujet: Re: prove that Sam 09 Jan 2010, 20:22 | |
| on a xyz = 1
==) a = sup (x;y;z) sup à 1
(a/a-1)^2 sup ou égal à 1
C.Q.F.D | |
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: prove that Sam 09 Jan 2010, 20:41 | |
| - {}{}=l'infini a écrit:
- on a xyz = 1
==) a = sup (x;y;z) sup à 1
(a/a-1)^2 sup ou égal à 1
C.Q.F.D 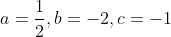  La condition d'être des réels positifs aurait pu évidemment radicalement simplifier le problème. | |
|
{}{}=l'infini
Expert sup
Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
| | Sujet: Re: prove that Sam 09 Jan 2010, 20:45 | |
| oui , je me dépeche toujours , bonne remarque ! | |
|
Thalès
Expert grade1
Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
| | Sujet: Re: prove that Ven 26 Fév 2010, 15:06 | |
| | |
|
