| | limite complique |  |
|
+8kobica achraf_djy master oussama1305 mehdi-47 zakariaforever Othmaann Pedro thunder 12 participants |
|
| Auteur | Message |
|---|
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: limite complique Sujet: limite complique  Dim 14 Mar 2010, 11:26 Dim 14 Mar 2010, 11:26 | |
| demontrer que
lim(x-->0)(tanx-x)/x^3=1/3 | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 12:04 Dim 14 Mar 2010, 12:04 | |
| tu as déja la reponse tu peux donc utiliser la définition de limite c'est à dire : (\exists%20\alpha%20%3E0)(\forall%20x\in%20D_f):%20|x|%3C\alpha\Rightarrow%20|f(x)-\frac{1}{3}|%3C\epsilon) a partir de lencadrement de f , tu trouves un encadrement de x ensuite tu exprimes alfa en fonction de epsilon et cest bon ! | |
|
  | |
zakariaforever
Féru
 Nombre de messages : 33 Nombre de messages : 33
Age : 31
Date d'inscription : 12/03/2010
 | |
  | |
mehdi-47
Féru
 Nombre de messages : 37 Nombre de messages : 37
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 13:45 Dim 14 Mar 2010, 13:45 | |
| facile on va utiliser l'hopital^^ | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 15:02 Dim 14 Mar 2010, 15:02 | |
| - mehdi-47 a écrit:
- facile on va utiliser l'hopital^^
C'est pratique, mais hors-programme malheureusement. - Pedro thunder a écrit:
- demontrer que
lim(x-->0)(tanx-x)/x^3=1/3 Cette limite est un peu compliquée, à part la définition (cf. zakariaforever), ou le développement limité (programme prépas) tu n'a pas d'autre alternatives. Il existe beaucoup de limites telles que la tienne, comme : 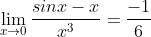 | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 17:23 Dim 14 Mar 2010, 17:23 | |
| bsr : bonne exo pedro voila ce que je l'ai trouve je suis pas sur si il est vrais :
(limx==>0) (tanx - x)/x^3 -1/3 =(limx==>0) 3tanx -3x -x^3/3x^3
et on a : 3tanx-3x-x^3/3x^3 < 3tanx -3x-x^3
puisque (limx==>0)3tanx -3x-x^3 =0
donc (limsx==>0)3tanx -3x-x^3/3x^3 =0
ce qui conduit a : (limx==>0) (tanx -x)/x^3 -1/3=0
donc necesserement on aurait (limx==>0) tanx-x/x^3 =1/3
A+ | |
|
  | |
achraf_djy
Expert grade1

 Nombre de messages : 401 Nombre de messages : 401
Age : 33
Localisation : Rabat
Date d'inscription : 01/08/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 17:42 Dim 14 Mar 2010, 17:42 | |
| Salut!
D'abord je vais calculer la lim quand x tend vers 0 de f(x)=(sin(x)-x)/x^3
Ensuite je vais l'utiliser pour calculé la limite de ce sujet!
On a x tend vers 0, donc 2x tend aussi vers 0, d'ou ils ont la meme limite que je la note Y.
Or f(2x)=(sin(2x)-2x)/(2x)^3
=(2sin(x)cos(x)_2x)/8x^3
=(sin(x)cos(x)-x)/4x^3
=(sin(x)cos(x)-xcos(x)+xcos(x)-x)/4x^3
=cos(x)(sin(x)-x)/4x^3 -x(1-cos(x))/4x^3
=f(x)*cos(x)/4 -(1-cos(x))/4x²
Et on a lim quand x tend vers 0 de f(2x)= lim quand x tend vers 0 de f(x)
car 2x et x tend tout les deux vers 0
donc
Y=Y*1/4 -1/4*(1/2)
D'ou Y=-1/6
ça d'une part
Maintenant on calcule la mil quand x tend vers 0 de (Tan(x)-x)/x^3
On a
(tan(x)-x)/x^3=(sin(x)-xcos(x))/x^3cos(x)
=(sin(x)-xcos(x)+x-x)/x^3cos(x)
=(sin(x)-x)/x^3*cos(x) +x(1-cos(x))/x^3cos(x)
=(1/cos(x))*(sin(x)-x)/x^3 +(1/cos(x))*(1-cos(x))/x²
maintenat on calcule la limite
lim quand x tend vers 0 de (tan(x)-x)/x^3=(-1/6)*1 +1*1/2
=1/3
achraf-djy | |
|
  | |
kobica
Maître

 Nombre de messages : 74 Nombre de messages : 74
Age : 31
Date d'inscription : 29/04/2008
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 21:11 Dim 14 Mar 2010, 21:11 | |
| salut achraf_djy
le petit probleme de cette methode c'est tu n'a pa le droit de citer la limite de f(x) avant qu'on demontre qu'elle admet une limite | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 21:32 Dim 14 Mar 2010, 21:32 | |
| - master a écrit:
- bsr : bonne exo pedro voila ce que je l'ai trouve je suis pas sur si il est vrais :
(limx==>0) (tanx - x)/x^3 -1/3 =(limx==>0) 3tanx -3x -x^3/3x^3
et on a : 3tanx-3x-x^3/3x^3 < 3tanx -3x-x^3
puisque (limx==>0)3tanx -3x-x^3 =0
donc (limsx==>0)3tanx -3x-x^3/3x^3 =0
ce qui conduit a : (limx==>0) (tanx -x)/x^3 -1/3=0
donc necesserement on aurait (limx==>0) tanx-x/x^3 =1/3
A+ Aie aie aie ... Si c'est vrai, alors: 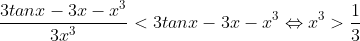 (En admettant que le dénominateur est positif au voisinage de 0+) Ce qui est totalement faux au voisinage de 0+ Réessayez ... | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 21:38 Dim 14 Mar 2010, 21:38 | |
| - master a écrit:
- bsr : bonne exo pedro voila ce que je l'ai trouve je suis pas sur si il est vrais :
(limx==>0) (tanx - x)/x^3 -1/3 =(limx==>0) 3tanx -3x -x^3/3x^3
et on a : 3tanx-3x-x^3/3x^3 < 3tanx -3x-x^3
puisque (limx==>0)3tanx -3x-x^3 =0
donc (limsx==>0)3tanx -3x-x^3/3x^3 =0(*)
ce qui conduit a : (limx==>0) (tanx -x)/x^3 -1/3=0
donc necesserement on aurait (limx==>0) tanx-x/x^3 =1/3
A+ Ta methode nest pas trés rigoureuse il ya des passages plutot louche , jmexplique : Pour pouvoir deduire que la limite (*) est egale à 0 il faut montrer quelle est superieur à 0 Et l'encadrement utilisé nest pas toujours vrai non plus! Et pour le dernier passage il n'est pas toujours vrai , meme si dans ce cas je pense que si. Je pense que pour que la lim f(x) - g(x) = lim f(x) - lim g(x) quand chacune des fonction f et g admet une limite déja et quelle soit finie | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 21:58 Dim 14 Mar 2010, 21:58 | |
| - achraf_djy a écrit:
- Salut!
D'abord je vais calculer la lim quand x tend vers 0 de f(x)=(sin(x)-x)/x^3
Ensuite je vais l'utiliser pour calculé la limite de ce sujet!
On a x tend vers 0, donc 2x tend aussi vers 0, d'ou ils ont la meme limite que je la note Y.
Or f(2x)=(sin(2x)-2x)/(2x)^3
=(2sin(x)cos(x)_2x)/8x^3
=(sin(x)cos(x)-x)/4x^3
=(sin(x)cos(x)-xcos(x)+xcos(x)-x)/4x^3
=cos(x)(sin(x)-x)/4x^3 -x(1-cos(x))/4x^3
=f(x)*cos(x)/4 -(1-cos(x))/4x²
Et on a lim quand x tend vers 0 de f(2x)= lim quand x tend vers 0 de f(x)
car 2x et x tend tout les deux vers 0donc
Y=Y*1/4 -1/4*(1/2)
D'ou Y=-1/6
ça d'une part
Maintenant on calcule la mil quand x tend vers 0 de (Tan(x)-x)/x^3
On a
(tan(x)-x)/x^3=(sin(x)-xcos(x))/x^3cos(x)
=(sin(x)-xcos(x)+x-x)/x^3cos(x)
=(sin(x)-x)/x^3*cos(x) +x(1-cos(x))/x^3cos(x)
=(1/cos(x))*(sin(x)-x)/x^3 +(1/cos(x))*(1-cos(x))/x²
maintenat on calcule la limite
lim quand x tend vers 0 de (tan(x)-x)/x^3=(-1/6)*1 +1*1/2
=1/3
achraf-djy Je pense que ce qui est en rouge est faux ( po sur ) mais d'après ce que je sais tu n'as pas le droit de changer certaine variable de ta limite en constante et de laisser d'autre variables tel qu'elles sont !! | |
|
  | |
achraf_djy
Expert grade1

 Nombre de messages : 401 Nombre de messages : 401
Age : 33
Localisation : Rabat
Date d'inscription : 01/08/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 22:20 Dim 14 Mar 2010, 22:20 | |
| Salut!
pour darkpseudo ce que je fait c'est totalement juste !
Cette méthode est juste!!!! | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Dim 14 Mar 2010, 22:55 Dim 14 Mar 2010, 22:55 | |
| On peut (presque) jamais etre sur d'une démonstration en maths surtout quand ya des calculs ... Mais ce que t'as fait ca me parait juste , sauf qu'il faut faire intervenir une autre limite qu'il faut connaitre à l'avance ! | |
|
  | |
achraf_djy
Expert grade1

 Nombre de messages : 401 Nombre de messages : 401
Age : 33
Localisation : Rabat
Date d'inscription : 01/08/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 07:01 Lun 15 Mar 2010, 07:01 | |
| Mais est ce que vous avez trouvé une erreur?
(pour f(x) on peut accépter qu'elle a une limite, s'elle exciste c'est Y)!!! | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 15:08 Lun 15 Mar 2010, 15:08 | |
| we we les gars merci ,c'est pour cela j'ai dis que je suis pas sur 100% | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 18:43 Lun 15 Mar 2010, 18:43 | |
| ok je viens de presenter autre methode avec l'hopitale: on appliquant le theoreme l'hopital on deduit  (tgx -x)/x^3)'=1+tg²x/3x² et on a : (1+tg²x/3x²)' = 2tgx/6x= tgx/3x (tgx/6x)'=1+tg²x/3 alors limx==>0 1+tg²x/3 = 1/3 j'espere qu'il soit cette fois vrais A+ | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 18:47 Lun 15 Mar 2010, 18:47 | |
| | |
|
  | |
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 18:56 Lun 15 Mar 2010, 18:56 | |
| L'hopitale dit que
lim x-->a[f(x)/g(x)]=f'(x)/g'(x)
alors
lim x-->0[(tanx-x)/x^3]=(tan0 - 0)/0^3 ????? | |
|
  | |
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 18:57 Lun 15 Mar 2010, 18:57 | |
| la methode de achraf_djy est la bonne | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Lun 15 Mar 2010, 19:14 Lun 15 Mar 2010, 19:14 | |
| bsr pedro thunder pour l'hopital on a lim x==>a f(x)/g(x)=limx==>a f'(x)/g'(x) =limx==>a f''(x)/g''(x) ......=L
ou est la faute ??? dans la demonsration | |
|
  | |
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Mar 16 Mar 2010, 11:01 Mar 16 Mar 2010, 11:01 | |
| lim x-->a[f(x)/g(x)]=f'(x)/g'(x)
pas
lim x-->a[f(x)/g(x)]=lim x-->a f'(x)/g'(x) | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Mar 16 Mar 2010, 12:10 Mar 16 Mar 2010, 12:10 | |
| slt pedro il te faut un peu reviser et maitriser ce loi je te donne ce lien ou tu peux le comprendre bien : http://fr.wikipedia.org/wiki/R%C3%A8gle_de_L%27H%C3%B4pital N.B: veulliez voire les exemples qui sont assez comme le tienne  | |
|
  | |
Miss imane
Féru

 Nombre de messages : 51 Nombre de messages : 51
Age : 32
Date d'inscription : 15/02/2010
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Mar 16 Mar 2010, 20:52 Mar 16 Mar 2010, 20:52 | |
| Bsr!
c'est juste ce qu'a fait master j'ai utilisé la meme methode et j'ai touvé que la limite est égale à 1/3. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Mar 16 Mar 2010, 22:14 Mar 16 Mar 2010, 22:14 | |
| Regardez l'exo 29 de Dima² . la règle de l'hopital y figure .  | |
|
  | |
albertmath
Féru

 Nombre de messages : 41 Nombre de messages : 41
Age : 30
Localisation : taourirt
Date d'inscription : 01/11/2008
 |  Sujet: Re: limite complique Sujet: Re: limite complique  Mer 17 Mar 2010, 17:59 Mer 17 Mar 2010, 17:59 | |
| on peut la calculé seulement par l'application de la définition | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: limite complique Sujet: Re: limite complique  | |
| |
|
  | |
| | limite complique |  |
|
