Nouveau JOPSM

Sujet: Nouveau JOPSM Lun 29 Mar 2010, 18:59

Bonsoir
j'ai aimé l'initiative de MOHE et de houssam110 pour l'idée du JOPSM c pour cela j'ai posté ce test:
j'accepterai toutes les solution reçues dans les 24 heures qui suivent:
EXERCICE 1:
a,b,c,d>0
Démontrer que parmi ces inégalités
(a+b)cd<ab(c+d) , (a+b)(c+d)<ab+cd , a+b<c+d
il y a au moins une incorrecte.
EXERCICE 2:
Le cercle inscrit dans le triangle ABC touche le côté [AC] en K
Démontrer que la droite qui joint le milieu du côté [AC] au centre du cercle inscrit coupe le segment [BK] en son milieu
EXERCICE 3:
Démontrer que l'équation 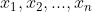$Nouveau JOPSM Gif$ admet une solution (x,y) dans Z pour un nombre infini d'entiers premier $Nouveau JOPSM Gif$
EXERCICE 4 :
$Nouveau JOPSM Gif.latex?x_{1},x_{2},..$ avec 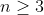$Nouveau JOPSM Gif$ sont de réels strictement positifs tels que 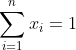$Nouveau JOPSM Gif$
Démontrer que $Nouveau JOPSM Gif.latex?x_{1}^{2}x_{2}+x_{2}^{2}x_{3}+..$
BONNE CHANCE !

Sujet: Re: Nouveau JOPSM Mer 31 Mar 2010, 13:06

imanos a écrit:: EXERCICE 1:
a,b,c,d>0
Démontrer que parmi ces inégalités
(a+b)cd<ab(c+d) , (a+b)(c+d)<ab+cd , a+b<c+d
il y a au moins une incorrecte.

Un exercice intéréssant, mais peut-être plus accomodé pour les tronc communs.

Spoiler:

Sujet: Re: Nouveau JOPSM Mer 31 Mar 2010, 13:14

oussama1305 a écrit:: Un exercice intéréssant, mais peut-être plus accomodé pour les tronc communs.

c'est vrai qu'il est facile.,mais mr oussama il faut quand même ne pas voir seulement le premier exercice et juger.par exemple le dernier exercice n'est pas facile du tout;c'est une généralisation d'une inégalité qui etait tjs connue par sa difficulté...

Sujet: Re: Nouveau JOPSM Mer 31 Mar 2010, 15:38

Bonjour à tous,
Solution du problème 4:
V: indique (quelque soit)
Soit P_n l'expression suivante, P_n: (Vn£n)(Vx_i£IR+) tels que: sum x_i = 1 /i={1,2,...,n},
on a: x_1²x_2+...+x_n²x_1=<4/27
prouvons que, P_{n}=>P_{n+1}
P_{n+1} : (Vn£n)(Vx_i£IR+) tels que:
sum x_i = 1 /i={1,2,...,n,n+1},
on a: x_1²x_2+...+x_n²x_{n+1}+x_{n+1}²x_1=<4/27.
Tout d'abord, l'inégalité est cyclique supposons que: pour tous i£{1,3,...,n+1} x_2>=x_3>=x_i
alors, on a:
x_1²x_2+...+x_n²x_{n+1}+x_{n+1}²x_1
=x_1²x_2-2x_1x_2x_3-x_3x_2²+ [x_3(x_1+x_2)²+...+x_{n+1}.(x_1+x_2)]-x_2x_{n+1}
=<[(x_1+x_2)²x_3+...+x_{n+1}.(x_1+x_2)]=<4/27
car (x_1+x_2)+x_3+x_4+...+x_{n+1}=1.
d'où on deduit que P_{n} => P_{n+1}. il suffit alors de prouver P_n pour n=3, on posant 3x_1=a , 3x_2=b , 3x_3=c , l'inégalité devient,
a²b+b²c+c²a=< 4 avec a+b+c=3
celle-ci est facile, assez connu, et prouvable par plusieurs methodes, je vous propose l'une d'eux qui revient à un ami, et qui est très belle,
l'inégalité est cyclique, supposons que a=max{a,b,c}, alors,
a²b+b²c+c²a=< a²b + abc + c²a/2 + ca²/2=a(a+c)(b+c/2)= 4* a/2 * (a+c)/2 * (b+c/2) =< 4
d'où on deduit notre inégalité,
Egalité si et seulement si x_1=2/3 , x_2=1/3 , x_3=x_4=...=x_n=0.

Sujet: Re: Nouveau JOPSM Mer 31 Mar 2010, 16:12

Bonjour tt le monde
désolé pour le retard car j'ai voyagé et ma connexion marche plus
MAJDOULINE et MOHE ont pu faire 3/4
donc chacun de vous poste le prochain JOPSM
A+

MohE a écrit:: d'où on deduit notre inégalité,
Egalité si et seulement si x_1=2/3 , x_2=1/3 , x_3=x_4=...=x_n=0.

Mais x_1,x_2...x_n>0 !

Féru Nombre de messages : 54 Age : 32 Date d'inscription : 29/01/2009

salut,
c'est une erreur de la part de imanos car en revenant à l'origine de cette inégalité celle de x+y+z=1==>x²y+y²z+z²=<4/27 on trouve qu'il s'agit de réels positifs (et pas non nuls)
à imanos: veuillez corriger votre énoncé Wink

Solution du problème 3 :
Supposons que il existe un ensemble finis ( E ) de nombre premier p_{i} t.q :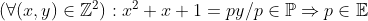
$Nouveau JOPSM P%5Cin%20%5Cmathbb%20P%20%5CRightarrow%20p%20%5Cin%20%5Cmathbb%20E$
Et posons :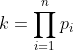
$Nouveau JOPSM %5C;%20%5Cforall%20i%5Cin%20%5Cleft%20%5C%7C%201,n%20%5Cright%20%5C%7C,p_%7Bi%7D%5Cin%20%5Cmathbb%20P%20%5Cright%20%5C%7D$
$Nouveau JOPSM Gif$
si k²+k+1 est premier alors :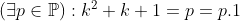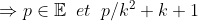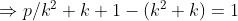
$Nouveau JOPSM Gif.latex?%28%5Cexists%20p%5Cin%20%5Cmathbb%20P%20%29:k%5E2+k+1=p=p$
$Nouveau JOPSM K%5E2+k+1$
$Nouveau JOPSM K%5E2+k+1-%28k%5E2+k%29=1$
Ce qui est absurde .
Avec un même raisonnement si k²+k+1 n'est pas premier on conclue que la supposition est fausse .
Alors il existe une infinité de nombre premier pour les quelles l'équation x²+x+1=py a une solution dans Z² .
Enfin , Sauf erreur ^^

» Nouveau Jopsm
» JOPSM - 2
» jopsm
» jopsm
» [b]le 14eme JOPSM[/b]