|
| | Nouveau Jopsm |  |
| | | Auteur | Message |
|---|
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Nouveau Jopsm Sujet: Nouveau Jopsm  Jeu 01 Avr 2010, 19:03 Jeu 01 Avr 2010, 19:03 | |
| Je crois que c'est deja l'heure de proposé un nv Jopsm,Problème 1.Soit E un ensemble des entiers naturels inferieurs ou égal a 100, c.à.d E={1,2,3,...,100}. prouvez que quelque soit 55 nombres choisi parmi E, il existe parmi eux, au moins deux nombres a_i et a_j, tels que a_j-a_i=12Problème 2.Soit n_1,n_2,...,n_{2012} des entiers positifs tels que:n_1²+n_2²+....+n_{2011}²=n_{2012}² Prouvez qu'au moins deux de ces nombres sont paires.Problème 3.Soit ABC un triangle acutangle tels que AB>AC et BÂC=60°. On note O le centre du cercle circonscrit du triangle ABC et H son orthocentre, la droite (OH) coupe [AB] en P et [AC] en Q. Prouvez que PQ=HQ.Problème 4.Soit a,b et c trois réel positifs. Prouver que:[(b+c-a)²]/[(b+c)²+a²] + [(a+c-b)²]/[(a+c)²-b²] + [(a+b-c)²]/[(a+b)²-c²]>= 3/5
Bonne Chance. P.S: j'accepterai toute solution reçu avant le vendredi 2 avril 20h00.- Spoiler:
N.B: Je n'ai proposé que des problèmes que j'ai trouvé sans solutions et que je l'ai resolu moi même, pour le deux, j'ai ajouter des choses aux problèmes original.
| |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Ven 02 Avr 2010, 22:54 Ven 02 Avr 2010, 22:54 | |
| Vainqueur: Dijkschneier; Score: 6/28.
Félicitations, à toi l'honneur de proposer le prochain Jopsm. | |
|   | | noirouge
Féru
 Nombre de messages : 54 Nombre de messages : 54
Age : 32
Date d'inscription : 29/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Sam 03 Avr 2010, 09:42 Sam 03 Avr 2010, 09:42 | |
| - MohE a écrit:
Problème 3.
[color=#8b0000]Soit ABC un triangle acutangle tels que AB>AC et BÂC=60°. On note O le centre du cercle circonscrit du triangle ABC et H son orthocentre, la droite (OH) coupe [AB] en P et [AC] en Q. Prouvez que PQ=HQ.
en dessinant la figure j'ai trouvé que O et H appartiennent à [PQ] ainsi on ne peut pas avoir PQ=HQ veux tu dire PO=HQ??????? | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Sam 03 Avr 2010, 10:28 Sam 03 Avr 2010, 10:28 | |
| - noirouge a écrit:
- MohE a écrit:
Problème 3.
[color=#8b0000]Soit ABC un triangle acutangle tels que AB>AC et BÂC=60°. On note O le centre du cercle circonscrit du triangle ABC et H son orthocentre, la droite (OH) coupe [AB] en P et [AC] en Q. Prouvez que PQ=HQ.
en dessinant la figure j'ai trouvé que O et H appartiennent à [PQ] ainsi on ne peut pas avoir PQ=HQ veux tu dire PO=HQ??????? Oui! c'était une faute de frappe, ca doit etre PO=QH. | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Sam 03 Avr 2010, 17:41 Sam 03 Avr 2010, 17:41 | |
| Exercie1bonjour.... je complète donc mon travail en postant la solution du premier exercice.....
on a E est l'union des deux ensemble A={1,2,3,....,96} et B={97,98,99,100}
remarquons que B ne contient aucun pair composé de deux entiers dont la différence est 12....essayons de trouver donc les pairs appartenant à A composés de deux entiers dont la différence est 12 ...c à d les pairs de forme (24k+n,24k+12+n) où 0≤k≤3 et 1≤n≤12 ainsi les nombres de ces pairs sont 12x4=48 pairs...ainsi en choisissant 55 élément de E on va choisir un certain nombre x parmi {1,2,3,....,96} et un certain y parmi {97,98,99,100} ...c à d x=55-y or y≤4 alors x≥51=48+3 ...ce qui prouve l'existence 3 pairs chacun est composé de deux éléments dont la différence est 12 ...ce qui est plus fort que ce qui est demandé
sauf erreur.... Exercice2: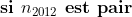 raisonnement par l'absurde: raisonnement par l'absurde: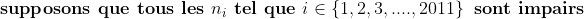 on a donc 2011 nombres impairs ce qui implique que la somme de leurs carrés est un nombre impair ce qui est absurde puisque 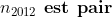 ainsi il existe au moins un n_{i} où i£{1,2,3,...,2011} qui est pair +n_{2012} qui est pair alors au moins deux des n_1,n_2,...,n_{2012} sont pairs CQFD ------------------------------------------------------------------------------------ 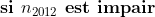 raisonnement par l'absurde: raisonnement par l'absurde: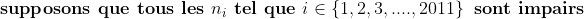 notons : +2011\Leftrightarrow%204\sum_{1}^{2011}(a_{i}^2+a_{i})+2011=4(n_{2012}^2+n_{2012})+1\Leftrightarrow%202005=2\left%20(n_{2012}^2+n_{2012}-\sum_{1}^{2011}(a_{i}^2+a_{i}%20\right%20)) alors 2 divise 2005 ce qui est absurde....ainsi au moins l'un des n_{i}(i£{1,2,3,...,2011}) est pair ....supposons qu'un seul nombre est pair alors la somme des carré des n_{i} sera un nombre pair ce qui est absurde car n_{2012} est impair.... alors au moins deux des n_1,n_2,...,n_{2011} est pair==>au moins deux des n_1,n_2,...,n_{2011},n_{2012} est pair ...CQFD --------------------------------------------------------------------------------- conclusion:dans tous les cas au moins deux des nombres n_{1},n_{2},..,n_{2012} sont pairs. -------------------------------------------------------------------------------- Exercice 3:(problème d'hébergement de Schéma) notons: (BH) coupe (AC) en M et (AH) coupe (BC) en I ..c à d: (BM) et (AI) sont hauteurs dans le triangle ABC ----------------------------------------------------- en considérant le triangle OBC(OB=OC) on a : 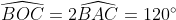 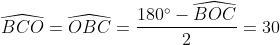 (a) d'autre part on a : 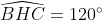 et on a : 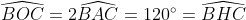 ainsi OHCB est circulaire........alors:(et en utilisant (a)) 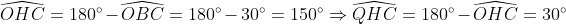 (1) en considérant le triangle BMC on a : 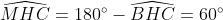 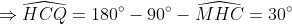 (2) de (1) et (2) on a donc: 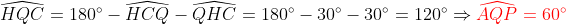 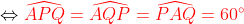 ==> PA=AQen considérant le triangle AIC on a : 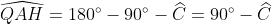 en considérant le triangle AOB (AO=OB)on a : 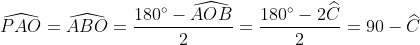 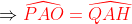 et on a : 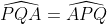 et AP=AQ alors les triangles AOP et AHQ sont isométriques d'où : PO=HQ ----------------------------------------------------------------------------------- Exercice4:voici ma solution que j'ai déja postée y a deux mois.... donc supposons que a+b+c=1(homogénéité) l'inégalité est équivalente à: ^2}{2a^2-2a+1}\geq\frac{3}{5}) \geq\frac{3}{5}<br />) 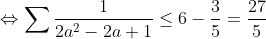 prouvons que : 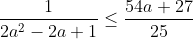 cela équivaut à : 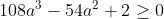 remarquons que 1/3 est une double racine et hop!!on obtient la factorisation: ^2(6a+1)\geq%200) ce qui est vrai...on a donc: 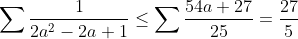 CQFD voir le lien: https://mathsmaroc.jeun.fr/inegalites-f2/easy-but-nice-t15389.htm?sid=797a6c396ed3bd7b10d35069364fcdee
Dernière édition par majdouline le Lun 05 Avr 2010, 21:56, édité 3 fois | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Dim 04 Avr 2010, 10:58 Dim 04 Avr 2010, 10:58 | |
| [quote="majdouline"] Exercice2: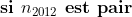 raisonnement par l'absurde: raisonnement par l'absurde: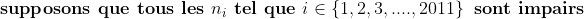 on a donc 2011 nombres impairs ce qui implique que la somme de leurs carrés est un nombre impair ce qui est absurde puisque 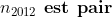 ainsi il existe au moins un n_{i} où i£{1,2,3,...,2011} qui est pair +n_{2012} qui est pair alors au moins deux des n_1,n_2,...,n_{2012} sont pairs CQFD ------------------------------------------------------------------------------------ 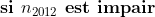 raisonnement par l'absurde: raisonnement par l'absurde: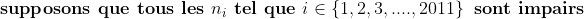 notons : +2011\Leftrightarrow%204\sum_{1}^{2011}(a_{i}^2+a_{i})+2011=4(n_{2012}^2+n_{2012})+1\Leftrightarrow%202005=2\left%20(n_{2012}^2+n_{2012}-\sum_{1}^{2011}(a_{i}^2+a_{i}%20\right%20)) alors 2 divise 2005 ce qui est absurde....ainsi au moins l'un des n_{i}(i£{1,2,3,...,2011}) est pair ....supposons qu'un seul nombre est pair alors la somme des carré des n_{i} sera un nombre pair ce qui est absurde car n_{2012} est impair.... alors au moins deux des n_1,n_2,...,n_{2011} est pair==>au moins deux des n_1,n_2,...,n_{2011},n_{2012} est pair ...CQFD --------------------------------------------------------------------------------- conclusion:dans tous les cas au moins deux des nombres n_{1},n_{2},..,n_{2012} sont pairs. -------------------------------------------------------------------------------- Exercice 3:(problème d'hébergement de Schéma) notons: (BH) coupe (AC) en M et (AH) coupe (BC) en I ..c à d: (BM) et (AI) sont hauteurs dans le triangle ABC ----------------------------------------------------- en considérant le triangle OBC(OB=OC) on a : 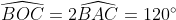 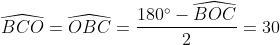 (a) d'autre part on a : 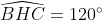 et on a : 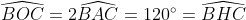 ainsi OHCB est circulaire........alors:(et en utilisant (a)) 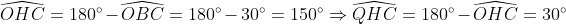 (1) en considérant le triangle BMC on a : 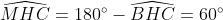 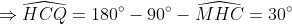 (2) de (1) et (2) on a donc: 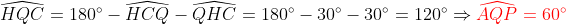 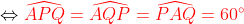 ==> PA=AQen considérant le triangle AIC on a : 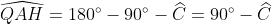 en considérant le triangle AOB (AO=OB)on a : 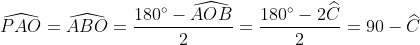 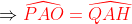 et on a : 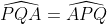 et AP=AQ alors les triangles AOP et AHQ sont isométriques d'où : PO=HQ ----------------------------------------------------------------------------------- Exercice4:voici ma solution que j'ai déja postée y a deux mois.... donc supposons que a+b+c=1(homogénéité) l'inégalité est équivalente à: ^2}{2a^2-2a+1}\geq\frac{3}{5}) \geq\frac{3}{5}br /) 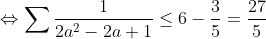 prouvons que : 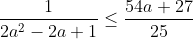 cela équivaut à : 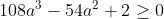 remarquons que 1/3 est une double racine et hop!!on obtient la factorisation: ^2(6a+1)\geq%200) ce qui est vrai...on a donc: 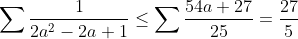 CQFD voir le lien: https://mathsmaroc.jeun.fr/inegalites-f2/easy-but-nice-t15389.htm?sid=797a6c396ed3bd7b10d35069364fcdee[/quote] Bonne travail majdouline  , j'ai lu les solutions des problems 2 et 4, c'est correctes, je n'ai pas lu celle de l'exo de geometri, mais je suis sur qu'elle serait aussi corrects , j'ai lu les solutions des problems 2 et 4, c'est correctes, je n'ai pas lu celle de l'exo de geometri, mais je suis sur qu'elle serait aussi corrects  . juste une remarque, lors d'un olympiade, n'oubli pas de noter que: 2a²-2a+1>0. . juste une remarque, lors d'un olympiade, n'oubli pas de noter que: 2a²-2a+1>0. | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Dim 04 Avr 2010, 14:20 Dim 04 Avr 2010, 14:20 | |
| bonjour.... voilà je viens d'éditer mon récent message pour poster la solution du premier exercice!!!  | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Dim 04 Avr 2010, 17:29 Dim 04 Avr 2010, 17:29 | |
| Ta solution pour le 1 est fausse, j'arrive pas a comprendre ce que tu as fais, disons qu'il 48 pairs, il se peut qu'on choisit de chaque couple l'un de ces termes qui serait plus loin de celui qu'on prendra du prochain couple, mais en tout cas j'arrive pas a bien comprendre, mais ce qui me pousse a dire que la solution est fausse, c'est qu'on peut pas prouver qu'il existe plus de deux nombres verifiant la relation, contrairement a ta solution qui prouve qu'il y a 4 nombres, alors que pour ce resultats il y a des contradiction, cherche encore... tu dois trouver d'autre solution. | |
|   | | noirouge
Féru
 Nombre de messages : 54 Nombre de messages : 54
Age : 32
Date d'inscription : 29/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Dim 04 Avr 2010, 20:11 Dim 04 Avr 2010, 20:11 | |
| aussi je n'arrive pas à comprendre la méthode de majdouline et je ne peux pas juger si c'est faux ou correct.mais mohE si elle a prouvé qu'il existe au moins 4 ça implique au moins 2,il n'y a pas de contradiction n'oublie pas qu'au moins 2=2 ou plus.
NB.mohE tu peux donner un ensemble inclus dans E contenant 55 éléments où il y a seulement 2 a_{i }et 2a_{j} comme contre exemple ,si tu crois fort bien que son raisonnement est faux. | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 07:20 Lun 05 Avr 2010, 07:20 | |
| - MohE a écrit:
- Ta solution pour le 1 est fausse, j'arrive pas a comprendre ce que tu as fais, , alors que pour ce resultats il y a des contradiction, cherche encore... tu dois trouver d'autre solution.
je le crois pas .... pas grave..quelle contradiction?!pas la peine! j'en ai une P.S.j'ai fait une toute petite erreur de calcul celle de 51=48+4 or 51=48+3 je viens de la corriger... et puis....le minimum c'est 3 ...et je suis capable de donner comme exemple un ensemble de 55 éléments où l'existence de ces 3 pairs(depuis mon raisonnement)...es tu donc capable de me donner un exemple où il y'a seulement deux pairs??(si ton raisonnement est vraiment correct).... sauf erreur.... | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 18:02 Lun 05 Avr 2010, 18:02 | |
| - majdouline a écrit:
- MohE a écrit:
- Ta solution pour le 1 est fausse, j'arrive pas a comprendre ce que tu as fais, , alors que pour ce resultats il y a des contradiction, cherche encore... tu dois trouver d'autre solution.
je le crois pas ....
pas grave..
quelle contradiction?!
pas la peine! j'en ai une
P.S.j'ai fait une toute petite erreur de calcul celle de 51=48+4 or 51=48+3
je viens de la corriger...
et puis....le minimum c'est 3 ...et je suis capable de donner comme exemple un ensemble de 55 éléments où l'existence de ces 3 pairs(depuis mon raisonnement)...es tu donc capable de me donner un exemple où il y'a seulement deux pairs??(si ton raisonnement est vraiment correct)....
sauf erreur.... Si! ta solution est fausse!Si! car je ne suis pas le seul à ne pas comprendre ta solution, on ne sait même pas de qu'elle principe s'agit ta solution?! et puis, le forume n'est pas fait pour proposer des solutions que les autres (peut-etre que personne) n'arivent pas a comprenerQuand même, je ne vais pas m'assoeoir ici, et essayer jusqu'a te trouver une contradiction, mais, lit ta solution une autre fois, tu as peut-etre prouvé qu'il existe 48 couple de la forme de (24k+n,24k+12+n) qui appartient tous a N, mais tu as bien oublié qu'il a des intersections entre ces couples, or nous on a pris des nombres distincts, aussi regarde bien ta solution, au debut tu parlais des couples, et dans la sixieme ligne, tu associ le resultat sur le nombres?!? oui on choisira x>=48+3 de E, mais tois tu prouver qu'il existe 48 couple par E et non plus parmi les choisi, je crois que tu as un peu confondu les choses.Tant pis!garde ta solution fausse, elle te servira très bien et pour longtemps.Là, tu me prouve, que tu t'es baser sur ta solutions sur des exemples qui peuvent être fausse, mais bon! On ne cherche pas un exemple, on cherche une solution pour le cas generalJuste pour tes infos, le problème n'est pas de cette facilté, ta solution fausse (sois-en sûre) le rend plus-que-facil. Ta solution pour l'inego m'as bien fasciné  | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 20:37 Lun 05 Avr 2010, 20:37 | |
| en tout cas je ne suis pas obligée de rester là en train d'expliquer mais crois moi..je crois fort bien (pas certaine ..enfin je n'étais jamais certaine) que ma solution est correcte ....je crois qu'en cherchant un minimum on peut distinguer le cas où ce minimum est atteint et ce que je veux moi c'est un cas où il n y a que 2 pairs... la seule chose que tu es en train de dire et de répéter c'est que ce n'est pas compréhensible or ce n'est pas vraiment un argument qui prouve que c'est faux.... par un petit contre exemple ou par une simple contradiction dans mon raisonnement je serai convaincue...sinon j'aime bien ma jolie solution! P.S.je me base rarement sur les exemple pour prouver le cas général!(et ici ce n'est pas le cas) amicalement  sinon je demande l'intervention d'un membre d'un plus haut niveau! | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 21:05 Lun 05 Avr 2010, 21:05 | |
| - majdouline a écrit:
- Exercie1
bonjour....
je complète donc mon travail en postant la solution du premier exercice.....
on a E est l'union des deux ensemble A={1,2,3,....,96} et B={97,98,99,100}
remarquons que B ne contient aucun pair composé de deux entiers dont la différence est 12....essayons de trouver donc les pairs appartenant à A composés de deux entiers dont la différence est 12 ...c à d les pairs de forme (24k+n,24k+12+n) où 0≤k≤3 et 0≤n≤12 ainsi les nombres de ces pairs sont 12x4=48 pairs...ainsi en choisissant 55 élément de E on va choisir un certain nombre x parmi {1,2,3,....,96} et un certain y parmi {97,98,99,100} ...c à d x=55-y or y≤4 alors x≥51=48+3 ...ce qui prouve l'existence 3 pairs chacun est composé de deux éléments dont la différence est 12 ...ce qui est plus fort que ce qui est demandé
sauf erreur....
J'espère que quelqu'un de haut niveau intervient dans ce topic pour resoudre ce quiproquo, en fait, ce qui est en rouge, ne doit-elle pas etre 13*4=52? , si oui, qu'est ce qu'il s'en suit?! et puis alors pourquoi si il existe 52 couples dans B=E\{96,97,98,100} (ou 48 couples), et qu'on retirera au moins 48+3 nombres de B, il existera 3couple verifiant l'ennoncé, il n'y a aucun relation entre l'argument 1 et l'argument 2 et la conclusion. , si oui, qu'est ce qu'il s'en suit?! et puis alors pourquoi si il existe 52 couples dans B=E\{96,97,98,100} (ou 48 couples), et qu'on retirera au moins 48+3 nombres de B, il existera 3couple verifiant l'ennoncé, il n'y a aucun relation entre l'argument 1 et l'argument 2 et la conclusion. | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 21:11 Lun 05 Avr 2010, 21:11 | |
| - MohE a écrit:
J'espère que quelqu'un de haut niveau intervient dans ce topic pour resoudre ce quiproquo, en fait, ce qui est en rouge, ne doit-elle pas etre 13*4=52? , si oui, qu'est ce qu'il s'en suit?! et puis alors pourquoi si il existe 52 couples dans B=E\{96,97,98,100} (ou 48 couples), et qu'on retirera au moins 48+3 nombres de B, il existera 3couple verifiant l'ennoncé, il n'y a aucun relation entre l'argument 1 et l'argument 2 et la conclusion. , si oui, qu'est ce qu'il s'en suit?! et puis alors pourquoi si il existe 52 couples dans B=E\{96,97,98,100} (ou 48 couples), et qu'on retirera au moins 48+3 nombres de B, il existera 3couple verifiant l'ennoncé, il n'y a aucun relation entre l'argument 1 et l'argument 2 et la conclusion. nn k peut prendre 4 valeurs le 0 le 1 le 2 et le 4.....et le i peut prendre 12 valeurs de 1 jusqu'à 12 ce qui fait au total 12x4=48 pairs je me demande d'où vient tu de 13x4=52???? pourquoi les3?? car on a trouvé que:au maximum 52 éléments a_{i}et a_{j}(qui appartiennent à E)qui ne réalisent pas la relation a_{i}-a_{j}=12 ..ce maximum 52 vient des 4 éléments de B qu'on peut prendre au maximum+ les 48 éléments sans leurs partenaires de l'ensemble A qu'on peut prendre au maximum .....je souhaite que c'est plus compréhensible  55=52+3...ce qui nous conduit vers ces 3 au moins!!! tout à fait!  | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 21:44 Lun 05 Avr 2010, 21:44 | |
| - majdouline a écrit:
- MohE a écrit:
J'espère que quelqu'un de haut niveau intervient dans ce topic pour resoudre ce quiproquo, en fait, ce qui est en rouge, ne doit-elle pas etre 13*4=52? , si oui, qu'est ce qu'il s'en suit?! et puis alors pourquoi si il existe 52 couples dans B=E\{96,97,98,100} (ou 48 couples), et qu'on retirera au moins 48+3 nombres de B, il existera 3couple verifiant l'ennoncé, il n'y a aucun relation entre l'argument 1 et l'argument 2 et la conclusion. , si oui, qu'est ce qu'il s'en suit?! et puis alors pourquoi si il existe 52 couples dans B=E\{96,97,98,100} (ou 48 couples), et qu'on retirera au moins 48+3 nombres de B, il existera 3couple verifiant l'ennoncé, il n'y a aucun relation entre l'argument 1 et l'argument 2 et la conclusion. nn k peut peut prendre 4 valeur le 0 le 1 le 2 et le 4.....et le i peut prendre 12 valeurs de 1 jusqu'à 12 ce qui fait au total 12x4=48 pairs je me demande d'où vient tu de 13x4=52????
pourquoi les3?? car on a trouvé que:au maximum 52 éléments a_{i}et a_{j}(qui appartient à E)qui ne réalisent pas la relation a_{i}-a_{j}=12 ..ce maximum 52 vient des 4 éléments de B qu'on peu prendre au maximum+ les 48 éléments sans leurs partenaires de l'ensemble A qu'on peut prendre au maximum .....je souhaite que c'est plus compréhensible 
55=52+3...ce qui nous conduit vers ces 3 au moins!!!
tout à fait!  4?! je crois que c'est plutôt 3. i? de qu'elle i parle tu? il n'y a pas de i dans ta solution, je crois que tu voulais dire n, de plus tu ecrit, 0=<k=<3 (4 valeurs pour k), et 0=<n=<12 (13 valeures pour n), en fait il y a 13*4-1 couples de cette forme. de plus t'as pas prouver qu'il existe au maximum 52 élèment qui ne verifient pas la relation a_i-a_j=12, mais plutôt 52 couples, qui -theoriquement- n'as rien avoir avec ce que tu as deduit. de plus comment ca 52 nombres vient de 4 element de B+ 48 de A, tu ne maximze pas les element pris B, mais tu assure qu'on aurra des (4) élèments de B, cequi n'as pas obligatoire,de plus, tu as ecrit que tu vas trouver le minimum qui verifie la relation dans A (ligne 4), <=> le maximum qui ne verifie pas la relation et qui appartient à A et qui ne verifie pas l'ennonce, et puis tu y inclus aussi B, c'est pas logique.Je repète que l'erreure de ta solution est que tu as travaillé sur les couples, puis tu a appliqué sur les nombres.  | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 21:59 Lun 05 Avr 2010, 21:59 | |
| absolument c'etait plutôt une erreur de frappe ce sont les n et non pas les i ....correction les n£{1,2,....12} (comme j'ai indiqué dans mon récent post) | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 22:10 Lun 05 Avr 2010, 22:10 | |
| t'as bien fais de corriger cette erreure, mais je vois encore que ta solution est fausse, elle est fausse. | |
|   | | noirouge
Féru
 Nombre de messages : 54 Nombre de messages : 54
Age : 32
Date d'inscription : 29/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Lun 05 Avr 2010, 22:42 Lun 05 Avr 2010, 22:42 | |
| bonsoir, quelle conversation!  j'arrive maintenant plus ou moins à comprendre .je vois qu'elle a commencé par considérer les pairs qui appartiennent à l'ensemble{(24k+n,24k+12+n}) avec les mêmes conditions de k et n qu'elle a considérées ,qui sont 48 pairs mais après la récente modification. et puis l'ensemble{97,98,100} pour former en union avec le précèdent ensemble l'ensemble E celui du départ. on retire 55 éléments de E alors on retire des élément des deux ensembles . le maximum de nombre d'éléments a_{i} qu'on peut choisir non accompagnés de leurs "partenaire" a_{j} sont les 3 de l'ensemble B qui peuvent être retirés sans leurs partenaires et puis les 48 éléments du premier ensemble sans qu'il soient accompagnés de leurs partenaires.52 élément en total. mais ta solution est vraiment louche Majdouline ,n'est pas bien présentée et pourtant je crois qu'elle est correcte. aussi ,je voudrais bien qu'un membre de haut niveau intervienne pour mieux parler de ce joli problème!et présenter encore d'autres solution à part celle de Majdouline!ou bien tout contredire et présenter la bonne solution. | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Mar 06 Avr 2010, 12:25 Mar 06 Avr 2010, 12:25 | |
| - noirouge a écrit:
- bonsoir,
quelle conversation! 
j'arrive maintenant plus ou moins à comprendre .je vois qu'elle a commencé par considérer les pairs qui appartiennent à l'ensemble{(24k+n,24k+12+n}) avec les mêmes conditions de k et n qu'elle a considérées ,qui sont 48 pairs mais après la récente modification.
et puis l'ensemble{97,98,100} pour former en union avec le précèdent ensemble l'ensemble E celui du départ.
on retire 55 éléments de E alors on retire des élément des deux ensembles .
le maximum de nombre d'éléments a_{i} qu'on peut choisir non accompagnés de leurs "partenaire" a_{j} sont les 3 de l'ensemble B qui peuvent être retirés sans leurs partenaires et puis les 48 éléments du premier ensemble sans qu'il soient accompagnés de leurs partenaires.52 élément en total.
mais ta solution est vraiment louche Majdouline ,n'est pas bien présentée et pourtant je crois qu'elle est correcte.
aussi ,je voudrais bien qu'un membre de haut niveau intervienne pour mieux parler de ce joli problème!et présenter encore d'autres solution à part celle de Majdouline!ou bien tout contredire et présenter la bonne solution. merci pour l'intervention, bon! du moins maintenant je commence a comprendre ce qu'elle a fait, mais, elle a ecrit que 0=<k=<3 et 1=<n=<12A alors contient 4*12=48 couples de la forme {(24k+n,24k+n+12)}, B n'en contient aucun, c'est vrai qu'on a E=AUB, mais seula ne veut pas dires que les nombres des couples sera ceux de A + ceux de B=48, il se peut qu'on y rajoute d'autre couples, en fait il y a beaucoup de couple a ajouter, par exemple (96,84). c'est a dire que E contient beaucoup plus que 48 couples.après; oui le maximum qu'on peut retiré de B est 3 élèments, mais 48 élèments de A n'aynt pas de partenaire, c'esl le minimum, tu peux bien le remarqué. @noirouge, je proposerai ma solution si tu la veux, sois par mp, sois dans ce topic même. comme tu veux. P.S: en fin, tant pis, que la solution sois bonne ou pas, ce dont j'insiste, c'est qu'elle était fausses (ou contenaits des erreures) et qu'on m'as pas modestement recueilli lorsque je l'ai signalé, alors, tant pis. | |
|   | | noirouge
Féru
 Nombre de messages : 54 Nombre de messages : 54
Age : 32
Date d'inscription : 29/01/2009
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  Mar 06 Avr 2010, 13:16 Mar 06 Avr 2010, 13:16 | |
| bonjour  oui c'est bien vrai que la solution de Majdouline contenait des erreurs ,exactement deux erreurs:celle de 51=48+4 ,et celle des n. Mais je crois que ce n'était que des erreurs d'inattention ,il est vrai aussi que la solution n'était pas bien claire et "louche" mais elle est jolie et je crois qu'elle est correcte. je veux aussi signaler à majdouline qu'elle doit plutôt expliquer sa solution et essayer de convaincre à la place de dire qu'elle "n'est pas obligée" j'aimerais bien que tu m'envoie ta solution par mp...en attendant encore l'intervention d'un autre membre! et pour l'exemple que tu as ajouté mohE (96,84) n'oublie pas qu'on cherche le maximum de couples n'ayant pas leur partenaires ,ce qui veut dire le minimum de couples de forme (i,i+12) c'est pour cela qu'elle a choisi de considérer précisément ces deux ensembles pour avoir le minimum de couples de forme (i,i+12)  | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Nouveau Jopsm Sujet: Re: Nouveau Jopsm  | |
| |
|   | | | | Nouveau Jopsm |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
