NOUVEAU TEST

Féru Nombre de messages : 66 Age : 30 Date d'inscription : 09/02/2010

EXERCICE 1:
on considère le polynom P(x) tel que
P(x)=ax²+bx+c / a£ IN et (b,c)£Z²
Trouver la valeur minimale de a pour laquelle il existe b,c tels que P(x) a 2 racines réeles distinctes appartiennet a ]0,1[
EXERCICE 2:
on a carré sa surface est égale a 4
un forgeron veut faire une boite de ce carré
trouver le volume maximal de cette boite
EXERCICE 3
Soient 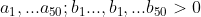$NOUVEAU TEST Gif.latex?a_{1},...a_{50};b_{1}...,b_{1},..$
MQ $NOUVEAU TEST Gif$
Exercice 4
soient x,y,z des côtés d'un triangle tels que
$NOUVEAU TEST Gif$
MQ
$NOUVEAU TEST Gif$
PS: L'ordre des exos n'a pa une relation avec le niveau de difficulté

Féru Nombre de messages : 54 Age : 32 Date d'inscription : 29/01/2009

bonjour Imanos,
je crois qu'il y a une petite erreur dans la dernière inégalité ,à toi de la corriger ,regarde le dénominateur du premier terme, Wink

Bonsoir...
• Exercice1:
P(x)=ax²+bx+c à deux racines réelles distinctes qui appartiennent à ]0,1[ alors :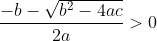
$NOUVEAU TEST Gif$ et puisque a>0 alors b<0 ...on réécrit donc le polynôme ainsi :
P(x)=ax²-bx+c où (a,b)£IN² et c£Z
on a donc :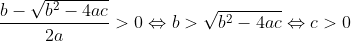
$NOUVEAU TEST Gif$
ainsi notre polynôme devient:P(x)=ax²-bx+c où (a,b,c)£IN³
on a : 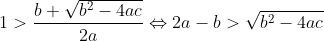$NOUVEAU TEST Gif$
on peut facilement remarquer que 2a>b ...
$NOUVEAU TEST Gif$
b²>4ac et 2a>b alors a>c et on a (a+c)²>b²>4ac alors entre (a+c)² et 4ac il existe au moins un entier d'où (a+c)²-4ac≥2 <=>(a-c)²≥2<=>(a-c)²≥4(car le carré parfait qui vient directement après 2 c'est 4)
d'où a-c≥2 d'où (2a-2)²≥(a+c)²>b² ==>2a>b+2
a-c≥2<=>a≥2+c et on a c≥1 alors a≥3...pour a=3
et on a 2a>b+2 alors b<4 d'autre part on a b²>4ac=12c alors b²>12>9
d'où b<4 et b>3 contradiction
a=4 on a 2a>b+2 alors 6>b et on a b²>4ac=16c>16 alors 6>b>4 alors b=5
et on a b²>16c alors 25/16>c d'où c=1 alors le polynôme devient
4x²-5x+1 qui a pour racine x=1==>contradiction ....
finalement pour a=5
et pour b=5 et c=1 (on prouve ici l'existence de b et c) c à d le polynôme:
P(x)=5x²-5x+1 a pour racines:
NOUVEAU TEST 1271017210754

et effectivement les deux racines appartiennent à ]0,1[!
--------------------------------------------------------------------------------------------------------------------------------------

•Exercice 3:
$NOUVEAU TEST Gif$
$NOUVEAU TEST Gif$
$NOUVEAU TEST Gif$
avec égalité si :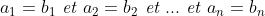
$NOUVEAU TEST Gif.latex?a_{1}=b_{1}\textit{%20et%20}a_{2}=b_{2}\textit{%20et%20}..$
-----------------------------------------------------------------------------------
•Exercice 4:
en posant :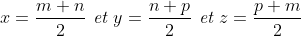
$NOUVEAU TEST Gif$
la condition 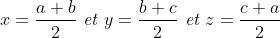$NOUVEAU TEST Gif$ devient :
mnp=8 et l'inégalité 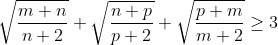$NOUVEAU TEST Gif$ devient:
$NOUVEAU TEST Gif$
encore un changement de variables ....
en posant : 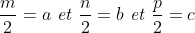$NOUVEAU TEST Gif$
la condition devient abc=1
et l'inégalité devient: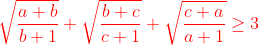
$NOUVEAU TEST Gif$
par Am-Gm on a :
NOUVEAU TEST 1271005842151

il suffit donc de prouver que :
(a+b)(b+c)(c+a)≥(a+1)(b+1)(c+1) ce qui équivaut à:a²b+b²a+b²c+c²b+c²a+a²c≥ab+bc+ca+a+b+c
Or d'après Cauchy Schwartz on a:
$NOUVEAU TEST Gif$
et puisque abc=1 alors :1/a=bc et 1/c=ab et 1/b=ac;d'où: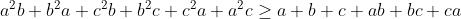
$NOUVEAU TEST Gif$
CQFD, avec égalité si et seulement si x=y=z=2
sauf erreur....

Féru Nombre de messages : 66 Age : 30 Date d'inscription : 09/02/2010

BONSOIR!!
BRAVO MAJdouline
POur le 4eme exercice BRAVO pour les chagements de vraiables
car pour faire cette inégalité j'ai pris celle en rouge (une inégalité de VASC) et j'ai fait (presque les meme chagements que t'as fait)
IL vous reste encore le 2eme Exercice!!

Bonsoir, j'ai pas pu participer et envoyer mes solutions, j'avoue cependant que j'ai trouvé des difficultés avec le premier exos, mais en fin trouver a=5. mais ma solutions est très longue.
Solution 2:
Soit V le volume de la boite, a,b,c ces dimensions dans l'espace, on a alors, 2(ab+bc+ca)=4 => ab+bc+ca=2
V=abc => V²= a²b²c²=(ab)(bc)(ac)=<[(ab+bc+ca)/3]^3=8/27
=> V=<(2V2)/(3V3), la boite du forgeron atteindra un volume maximal lorsqu'elle sera un cube de côté a=V2/V3.
Solution 3:
Juste multiplier les deux côté par 99, simplifier puis utiliser l'identité a²+b²>=2ab, pour trouver le resultats voulu.
Solution 4:
même methode qui est déjà cité, avec une différence dans la deuxième moitié.
Il suffit de prouver que (a+b)(b+c)(c+a)>=(a+1)(b+1)(c+1)
on pose q=ab+bc+ca et p=a+b+c et r=abc, il suffit donc de prouver que:
pq-r>=p+q+r+1 <=>pq-p>=q+3 <=>p(q-1)>=q+3
puisque p>=3 (Am-Gm), on a: p(q-1)>=3q-3>=q+3.
égalité si et seulement si a=b=c. ou encore, si le triangle du debut éait equilateral.

Féru Nombre de messages : 66 Age : 30 Date d'inscription : 09/02/2010

BRAVO A toi aussi MOHE
tu a utilisé IAG pour le 2eme exo
jlé résolu ainsi aisément
IL ya aussi une solution en utlisant la dérivation...
A+

avec la derivé, oui, ce problème peut-etre resolu en utilisant la derivation,
par symetrie de role supposons que a=<b=<c.
on ab+bc+ca=2 => c=(2-ab)/(a+b)
ainsi V=abc=ab(2-ab)/(a+b), on fixe b pour a et on pose:
f(a)=ab(2-ab)/(a+b), on trouve facilement que f'(a)=b²(2-ab)/(a+b)>=0, d'où f est croissante et ainsi, elle est maximal lorsque a est maximal, c.a.d a=V2/V3, or a ne peut atteindre cette valeure tant qu'il inferieur à b et inferieur à c sauf, et seulement sauf lorsque a=b=c=V2/V3, ainsi, on trouve
V_{max}= (2/3)(V2/V3)

Sauf erreure.

Salut! le problème deux est tellement inetéressent même si il est facile, mais, on peut tout de même le rendre plus délicat.
Extension du Problème n°2:
On se dispose d'un carré de surface S=a² où a est un réel non-negatif.
Peut-on découpez ce carré en exactement 6 morceaux, avec lesquels on pourrait construire une boite dont le volume est maximal.

Expert sup Nombre de messages : 1665 Age : 30 Date d'inscription : 05/03/2010

Ma solution de l'exercise N°1:

- On a: ax²+bx+c=0 a deux solutions distinctes, donc b²-4ac>0. (A)
* x1,x2 se trouvérent dans ]0,1[, donc 0<(-b-V(b²-4ac)/2a<1 (1) et 0<(-b+V(b²-4ac)/2a<1 (2)
* En sommant (1) et (2), on trouve: 0<-b/a<1 (M), donc -b<a (B) avec b<0 et a£|N*.
* De (A) et (B): a²>4ac donc a>=4c+1. (C)
* On a dans (1) : 2a>0, donc -b-V(b²-4ac)>0, par (M) -b>0 et par (A) V(b²-4ac)>0 D'ou: b²>b²-4ac => -4ac<0 => c>0 => c>=1. (H)
- Par (H) et (C) on déduit que: a>=5. Donc Min(a)=5.

ça veut dire quoi IAG ?

Expert sup Nombre de messages : 1004 Age : 31 Date d'inscription : 14/06/2010

inégalité arithmético-géométrique
AM-GM: pour tous réels positifs x1,x2....xn on a:
(x1+.....+xn)>= n . racine n ième de x1.x2....xn
[/i]

Merci Tarask pour ta réponse si rapide,je suis nouveau ici et je ne comprends pas encore les abréviations mathématiques utilisés...

Expert sup Nombre de messages : 1004 Age : 31 Date d'inscription : 14/06/2010

avec plaisir Yasser Very Happy

on est là pour s'entraider Very Happy

» un nouveau test d'ly pour vous
» Résultats du TDM -test 4 et test 5 -
» test
» TDM - test 2 - Problème 4
» TDM - Test 1