Exercice!

soit 2n+1 un carré complet (telle que n appartient a IN)
Démontrez que n+1 et la différence de 2 carrés complets!

W.Elluizi a écrit:

soit 2n+1 un carré complet (telle que n appartient a IN)
Démontrez que n+1 et la différence de 2 carrés complets!

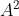
Un carré parfait n'est logiquement impair que si est impair. Et donc, par conséquent :
Déduisons donc que concernant le n de l'énoncé :
Et donc
Essayons de soupçonner quelque résultat. Nous avons :



Essayons de soupçonner la relation entre les k et les F sachant que
Nous avons d'après ce que nous avons déjà fait :

Il est donc fort probable que
Il est aussi intéressant de remarquer que
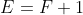
Et donc il est fort probable que
Ce qui est facilement prouvable par la suite en développant l'expression.
Comme vous pouvez le remarquer, ma méthode fait beaucoup appel à l'intuition.
Sauf erreur.
Au plaisir !

Pour ma part j'ai procéder autrement , au fait ce qui m'avais poser probléme c'est le fait que tout nombre impair est la différence de deux carrés parfait ( un ami me l'a rappeler )
déja prenons un carré parfait a^2
on a (a+1)^2 - a^2 = 2a+1 donc tout nombre impair est la différence de deux carré parfait !!
Il suffira de prouver que n+1 est impair
on a 2n+1 = (2k+1)^2
2n+1 = 4k^2+4k+1
2n+2 = 4k^2+4k+2
n+1 = 2(k^2+k) +1
qui est pair , ce qui conclu ^^

en fait,il faut juste prouver que n est pair!ce qui suit devient trop simple!!
2n+1=A²
alors:A=2k+1
ce qui implique :2n+1=4k²+4k+1
alors n=2(k²+k) supposons ke k²+k=S
donc : n+1=2S+1
et a la fin:n+1=(S+1)²-S²

Oui c'est ce que j'ai dis ^^ ! Merci pour l'exo

pas de quoi!!

J'ai la méme idée de Mr Elluizi. Merci bien pour l'exo.
Bonne chance.

avec plaisir!!