exo de suites

Débutant Nombre de messages : 4 Date d'inscription : 06/09/2006

soit (Un) une suite géométrique, son prmier terme est Uo=125, sa raison q=1/5.
1-calculer U1 et U2.
2- calculer S6=Uo+U1+U2+....+U5.
3- calculer Un en fonction de n, pour tout n de IN.
4- déterminer le plus petit entier naturel n tel que: Un < 10^-6
( 10 à la puissance -6).

je cherche une réponse concernant la 4 ème question. meri de votre aide. c urgent...

Expert sup Nombre de messages : 1595 Age : 65 Date d'inscription : 11/02/2007

BJR nki12 !!

D'abord tu prouves que Un=125.(1/5)^n
( c'est la question 3) )
Ensuite tu écris que Un={125/5^n} <10^(-6)
donc , puisque 125=5^3 , 5^(3-n) < 10^(-6)
d'ou 5^(n-3) > 10^6
et de là (n-3) Ln(5) > 6.Ln(10)
Conclusion : n > E(3 + 6.{Ln(10)/Ln(5)})+1
Le plus petit entier que tu cherches c'est N=E(3 + 6.{Ln(10)/Ln(5)})+1

Mnt à l'aide de ta Calculatrice ..... N=12

LHASSANE

Maître Nombre de messages : 234 Age : 31 Date d'inscription : 24/10/2009

nki12 a écrit:: soit (Un) une suite géométrique, son prmier terme est Uo=125, sa raison q=1/5.
1-calculer U1 et U2.
2- calculer S6=Uo+U1+U2+....+U5.
3- calculer Un en fonction de n, pour tout n de IN.
4- déterminer le plus petit entier naturel n tel que: Un < 10^-6
( 10 à la puissance -6).

je cherche une réponse concernant la 4 ème question. meri de votre aide. c urgent...

1\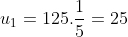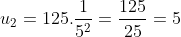
$exo de suites Gif.latex?u_{1}=12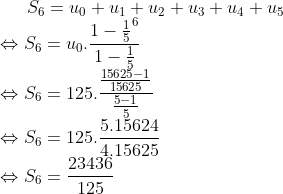5$
$exo de suites Gif.latex?u_{2}=125$

2\
$exo de suites Gif.latex?S_{6}=u_{0}+u_{1}+u_{2}+u_{3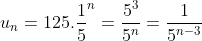}+u_{4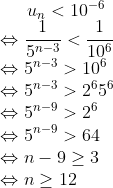}+u_{5}%20\\\Leftrightarrow%20S_{6}=u_{0}.\frac{1-\frac{1}{5}^6}{1-\frac{1}{5}}%20\\\Leftrightarrow%20S_{6}=125.\frac{\frac{15625-1}{15625}}{\frac{5-1}{5}}%20\\\Leftrightarrow%20S_{6}=125.\frac{5.15624}{4$

3\ $exo de suites Gif.latex?u_{n}=125$

4\
$exo de suites Gif$
n=12 est donc la réponse.

Sauf erreur.
Au plaisir ! Smile

ta utilisés ça 5^x > 5^y <=> x>y
pour que ca soit vrai il faut que la fonction 5^x soit une bijection croissante. Là je pense que c'est vrai , mais pour un autre exemple peut etre pas!

Débutant Nombre de messages : 4 Date d'inscription : 06/09/2006

merci les amis vous êtes vraiment gentils et serviables..

Othmaann a écrit:: ta utilisés ça 5^x > 5^y <=> x>y
pour que ca soit vrai il faut que la fonction 5^x soit une bijection croissante. Là je pense que c'est vrai , mais pour un autre exemple peut etre pas!

T'as entendu parler du logarithme de base 5?

Quand tu l'apprenais moi j'apprenais l'humilité ... bref , en + c'est pas besoin de logarithme de base 5 ici , le logarithme naturel suffira ... 5^x > 5^y <=> e^(xln5)> e^(yln5) <=> xln5 > yln5 ( c'est a ce moment là qu'intervient mon commentaire , pour pouvoir simplifier il faut que le nombre soit positif ce qui est vrai dans notre cas par contre pour 1/2 ca ne serais pas le cas )
Je voulais juste mettre en garde d'un passage pas tjr vrai ..!

Othmaann a écrit:: Quand tu l'apprenais moi j'apprenais l'humilité ... bref , en + c'est pas besoin de logarithme de base 5 ici , le logarithme naturel suffira ... 5^x > 5^y <=> e^(xln5)> e^(yln5) <=> xln5 > yln5 ( c'est a ce moment là qu'intervient mon commentaire , pour pouvoir simplifier il faut que le nombre soit positif ce qui est vrai dans notre cas par contre pour 1/2 ca ne serais pas le cas )
Je voulais juste mettre en garde d'un passage pas tjr vrai ..!

Personne ne me l'avait faite celle-là, mais félicitations, tu m'a cassé.

» Les suites: Les suites adjacentes. (2)
» suites
» suites
» Suites
» suites