Arithmétiques et raisonnement par absurde:

1/Montrez que si n+1 est un carré parfait.
Alors 14n+50 est la somme de quatre carré parfait.
2/Montrez que le nombre 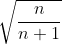n'est pas rationel avec n appartient à IN.
3/Montrez que 100010001 et 1000001 ne sont pas premiers.
4/Résolvez en IN: .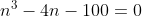
5/Trouvez tous les valeurs de n de IN, pour lesquels 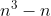soit divisible par n-3.
Bonne chance.

slt , je crois que t'a oublie dans deuxieme exo que n£N* , sinon tu auras une contradiction !! ^^

master a écrit:

slt , je crois que t'a oublie dans deuxieme exo que n£N* , sinon tu auras une contradiction !! ^^

Bien sûr.
C'est édité.

ok , meme si pas bien edité car il te faut N* ^^
donc supposons que Vn/n+1 rationnelt alors :

n=a² et n+1=b² ==> (b-a)(b+a)=1==> b=1 et a=0
alors n/n+1 =0 ==> n=0 => absurde
et deuxieme facon vous pouver essayer avec (valuation p-adique)
et vous trouver que la valiation su nombre n/n+1 est positif et d'ou la conclusion....

pour troisieme il suffit de remarquer que
1000001=1000000+1=10^6 + 1 =10^6 + 1^6 =(10+1)(10^5 +-.....-1) donc n'est pas premier
de meme pour l'autre

Je términe ce qu'à débuter Mr master:

Pour le premier:
Montrez que si n+1 est un carré parfait.
Alors 14n+50 est la somme de quatre carré parfait.
------------------------------------------------------------

14n+50=9(n+1)+4(n+1)+36+1
=> 14n+50=(3a)²+(2a)²+6²+1²

Bonne chance.

slt marjani , j'ai ete entrain d'ecrire le meme soluc ^^ , mais ...tu l'a posté avant moi ^^ !! en tt cas b1 .

master a écrit:

pour troisieme il suffit de remarquer que
1000001=1000000+1=10^6 + 1 =10^6 + 1^6 =(10+1)(10^5 +-.....-1) donc n'est pas premier
de meme pour l'autre

Pour celui-là, c'est juste.
On ne peut pas procéder de même pour l'autre.

M.Marjani a écrit:

Je términe ce qu'à débuter Mr master:
Pour le premier:
Montrez que si n+1 est un carré parfait.
Alors 14n+50 est la somme de quatre carré parfait.
------------------------------------------------------------
14n+50=9(n+1)+4(n+1)+36+1
=> 14n+50=(3a)²+(2a)²+6²+1²
Bonne chance.

Ou bien:
On a 14n+50=14n+14+36.
Donc 14n+50=14(n+1)+36.
Donc 14n+50=14a^2+6^2.
Donc 14n+50=a^2+4a^2+9a^2+6^2.
Donc 14n+50=a^2+(2a)^2+(3a)^2+6^2.
CQFD.

master a écrit:

pour troisieme il suffit de remarquer que
1000001=1000000+1=10^6 + 1 =10^6 + 1^6 =(10+1)(10^5 +-.....-1) donc n'est pas premier

On pourra écrire encore 1000001=1000000+1.
Donc 1000001=10^6+1.
Donc 1000001=(10^2)^3+1^3.
Donc 1000001=(10^2+1)(10^4-10^2+1).
Donc 1000001 n'est pas premier, car il admet au moins deux diviseurs.

nmo a écrit:

master a écrit:

pour troisieme il suffit de remarquer que
1000001=1000000+1=10^6 + 1 =10^6 + 1^6 =(10+1)(10^5 +-.....-1) donc n'est pas premier
de meme pour l'autre

Pour celui-là, c'est juste.
On ne peut pas procéder de même pour l'autre.

On a 100010001=100000000+10000+1.
Donc 100010001=10^8+10^4+1.
Donc 100010001=(10^2)^4+(10^2)^2+1.
Donc 100010001=(10^2)^4+(10^2)^2+1+(10^2)^2-(10^2)^2.
Donc 100010001=((10^2)^2)^2+2*(10^2)^2+1-(10^2)^2.
Donc 100010001=((10^2)^2+1)^2-(10^2)^2.
Donc 100010001=((10^2)^2+1-10^2)((10^2)^2+1+10^2).
Donc 100010001 n'est pas premier, car il admet au moins deux diviseurs.
Sauf erreur de frappe.

Pour le 4:
On a n^3-n=n(n²-1).
Donc n^3-n=n(n-1)(n+1).
On a n est un entiers naturel quelquonque.
Le reste de la division euclidienne de ce n sur 3 peut être 0, 1, ou 2.
On peut écrire n=3k ou n=3k+1 ou n=3k+2.
Si n=3k.
Donc n(n+1)(n-1)=3*k(n+1)(n-1).
Ainsi n^3-n et divisible par 3.==>(1)
Si n=3k+1.
Alors n-1=3k.
Donc n(n+1)(n-1)=3*k(n+1)n.
Ainsi n^3-n et divisible par 3.==>(2)
Si n=3k+2.
Alors n+1=3k+1+2.
Donc n+1=3k+3.
Donc n+1=3(k+1).
Donc (n+1)(n-1)n=3*n(k+1)(n-1).
Ainsi n^3-n et divisible par 3.==>(3)
De 1, 2, et 3 on conclut que n^3- est divisible par 3 quelquesoit n de IN.
Posons n^3-n=3m tel que m est un naturel.
On a n^3-4n-100=0.
Donc n^3-n-3n=100.
Donc 3m-3n=100.
Donc 3(m-n)=100.
Donc 100 est multiple de 3.
Ce qui est faux.
Ainsi l'équation n'admet aucune solution dans IN.
Sauf erreur.

Pour le 5:
Posons t=n-3 tel que t est un élément de IN.
Donc n=t+3.
On a n^3-3=(t+3)^3-3.
Donc n^3-3=t^3+9t^2+27t+27-3.
Donc n^3-3=t^3+9t^2+27t+24.
Si t divise t^3+9t^2+27t+24.
Donc t divise 24.
Donc t=1 ou t=2 ou t=3 ou t=4 ou t=6 ou t=8 ou t=12 ou t=24.
Si t=1, alors n=1+3.
Donc n=4.
Si t=2, alors n=2+3.
Donc n=5.
Si t=3, alors n=3+3.
Donc n=6.
Si t=4, alors n=4+3.
Donc n=7.
Si t=6, alors n=6+3.
Donc n=9.
Si t=8, alors n=8+3.
Donc n=11.
Si t=12, alors n=12+3.
Donc n=15.
Si t=24, alors n=24+3.
Donc n=27.
Pour que n-3 divise n^3-3, il faut que n=4 ou n=5 ou n=6 ou n=7 ou 9 ou n=11 ou n=15 ou n=27.
Sauf erreur.

J'ajoute celui-ci de géométrie:
Soit une droite xx' et deux points A et B de cette droite.
Montrez que pour tut point M du plan, MA+MB=AB équivaut à M appartien au seqment [AB].
Bonne chance.

nmo a écrit:

J'ajoute celui-ci de géométrie:
Soit une droite xx' et deux points A et B de cette droite.
Montrez que pour tut point M du plan, MA+MB=AB équivaut à M appartien au seqment [AB].
Bonne chance.

MA+MB=AB<=> AB²=MA²+MB²+2MA.MB=MA²+MB²-2MA.MA.cos(AMB)
<=> Cos (AMB)=- 1
D'où le résultat .

nmo a écrit:

J'ajoute celui-ci de géométrie:
Soit une droite xx' et deux points A et B de cette droite.
Montrez que pour tut point M du plan, MA+MB=AB équivaut à M appartien au seqment [AB].
Bonne chance.

Bonsoir;

On peut tracer une droite sur laquelle on met deux points A et B, puis on choisi un point M de l'espace(pas dans SATURNE ).
Dans le triangle AMB on a d'aprés le theoréme d'Alkachi: AB²=AM²+BM²-2AM*BM*Cos(M) (1)
Et d'aprés les donnés on a: MA+MB=AB <=> AB²=MA²+MB²+2MA*MB (2)
D'aprés (1) et (2) on a: Cos(M)=-1 <=> (Angle)M=180° (3).
(3) implique que M£[AB].
Au plaisir

Oui Mr MoH. Or, il ya d'autres methodes. On peut remarquer par EX que:
(Angle)M=180° (3).
(3) implique que M£[AB].

(Angle)M=180° le point M doit appartenir au segement [AB].
Sinon, (Angle)M=0°.

nmo a écrit:

J'ajoute celui-ci de géométrie:
Soit une droite xx' et deux points A et B de cette droite.
Montrez que pour tut point M du plan, MA+MB=AB équivaut à M appartien au seqment [AB].
Bonne chance.

Essayez de le résoudre par absurde.

Soit M un point appartenant au segement [AB]. Donc: AMB=180°.
(Vecteurs)AB=AM+MB <=> AB²=AM²+MB²+2AM*AB(vecteurs).
On a: (vecteurs) AM*MB=AM*MB(sanc vec) [(vec)AM,MB ont le méme sense. et M£[AB]]
=> AB²=AM²+MB²+2AM*MB (sans vec)
=> AB²=(AM+MB)²
=> AB=AM+MB.
Fini.
CQFD.

nmo a écrit:

J'ajoute celui-ci de géométrie:
Soit une droite xx' et deux points A et B de cette droite.
Montrez que pour tut point M du plan, MA+MB=AB équivaut à M appartient au seqment [AB].
Bonne chance.

Je réponds:
Supposons que MA+MB=AB et que M n'appartient pas à [AB].
Alors M est soit sur la demi-droite ouverte ]Ax'[, soit sur la demi-droite ouverte ]Bx[, soit non-aligné avec A et B.
(]xx'[ est un axe contenant A et B).
Si M appartient à la demi-droite ouverte ]Ax'[, tel que M'.
On a M'A+M'B=M'A+M'A+AB.
Donc M'A+M'B=2M'A+AB.
Et donc M'A+M'B#AB.
En contradiction avec l'hypothèse MA+MB=AB.
De même si M appartient à ]Bx[.
Si M n'est pas alligné avec A et B, on sait que dans le triangle non-aplati MAB, on a MA+MB>AB.
Ce qui contredit encore l'hypothèse.
On déduit intuitivement que M n'appartient pas à [AB] est impossible lorsque MA+MB=AB.
Autrement dit, le principe du raisonnement par l'absurde s'applique.
Et ainsi MA+MB=AB implique que M appartient à [AB].
Comme la réciproque M appartient à [AB] implique que MA+MB=AB, est vraie, également.
Le résultat voulu en découle.

Un exercice de plus:
Soient a et b deux entiers naturels non nuls, tel que a>b.
Démontrez que 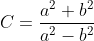n'est pas un entier.
Bonne chance.

M.Marjani a écrit:

nmo a écrit:

master a écrit:

pour troisieme il suffit de remarquer que
1000001=1000000+1=10^6 + 1 =10^6 + 1^6 =(10+1)(10^5 +-.....-1) donc n'est pas premier

On pourra écrire encore 1000001=1000000+1.
Donc 1000001=10^6+1.
Donc 1000001=(10^2)^3+1^3.
Donc 1000001=(10^2+1)(10^4-10^2+1).
Donc 1000001 n'est pas premier, car il admet au moins deux diviseurs.

Bonjour;
On peut également remarquer que: 1000001=(10^2+1)(10^4-10^2+1) pair > 2 , ce qui implique qu'il n'est guére un nombre premier.

Mais 1000001 n'est guère un pair!!!

W.Elluizi a écrit:

Mais 1000001 n'est guère un pair!!!

Faute de frappe, EDIT: IMPAIR : )

Attendez un solution pour l'EX de nmo.