| | Arithmétiques et raisonnement par absurde: |  |
|
+5MohE Sylphaen M.Marjani master nmo 9 participants |
|
| Auteur | Message |
|---|
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 20:27 Ven 03 Sep 2010, 20:27 | |
| Et bain alors ta réponse n'est pas correcte,c'est plutôt X pair et supérieur à 2 qui implique que X n'est pas premier! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 20:47 Ven 03 Sep 2010, 20:47 | |
| - W.Elluizi a écrit:
- Et bain alors ta réponse n'est pas correcte,c'est plutôt X pair et supérieur à 2 qui implique que X n'est pas premier!
 Non W.Elluizi, ce que t'as dis n'a aucun sens ^^ X un nombre premier est un nombre impair si et si que X>2. PS: Il ne s'agit pas d'une réponse à l'exercise. (Je hate reprendre mes solutions d'antan :d) | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 20:55 Ven 03 Sep 2010, 20:55 | |
| Je n'ai pas bien compris ce que tu essai de dire!Reformule! | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 21:01 Ven 03 Sep 2010, 21:01 | |
| Contre exemple:9 impaire et supérieur à 2,mais ce n'est tout de meme pas un nombre premier!
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 21:08 Ven 03 Sep 2010, 21:08 | |
| - nmo a écrit:
- Un exercice de plus:
Soient a et b deux entiers naturels non nuls, tel que a>b.
Démontrez que 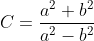 n'est pas un entier. n'est pas un entier.
Bonne chance. Indice: - Spoiler:
utilisez ce qui suit (d=pgcd(a,b) a=da' et b=db' tel que a'^b'=1) ça va surement mener à une solution 
bonne continuation  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 22:28 Ven 03 Sep 2010, 22:28 | |
|
Dernière édition par M.Marjani le Ven 03 Sep 2010, 23:14, édité 1 fois | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 22:43 Ven 03 Sep 2010, 22:43 | |
| petite remarque: on ne peut pas dire que t est de Q que si a et b sont premiers entre eux  et m=c+1  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 23:16 Ven 03 Sep 2010, 23:16 | |
| - tarask a écrit:
- petite remarque: on ne peut pas dire que t est de Q que si a et b sont premiers entre eux

et m=c+1  Oui, bonne remarque. Les légeres fautes de frappe ^^ La solution reste juste. | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Ven 03 Sep 2010, 23:53 Ven 03 Sep 2010, 23:53 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Un exercice de plus:
Soient a et b deux entiers naturels non nuls, tel que a>b.
Démontrez que 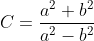 n'est pas un entier. n'est pas un entier.
Bonne chance.
Ma Solution:
+b^2\left ( 1+c \right )=0\Leftrightarrow \frac{c+1}{c-1}=(\frac{a}{b})^2)
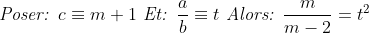
m et m-2 ne peuvent pas étre deux carrés en méme temps Car: 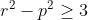 Pour tout Pour tout \varepsilon \mathbb{N})
Donc il n'existe pas de couple solution pour l'équation du départ. D'ou 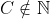 Je ne parle pas de ce cas-là, mais deux nombres peuvent ne pas être des carrés, mais leur fraction, oui; Et j'insiste sur "pas ce cas-là". Par exemple 18 et 2 ne sont pas des carrés, mais 18/2 = 9 = 3² oui. Une autre méthode pour résoudre l'exercice. Supposons que la fraction est vraiment un entier c, et supposons que PGDC(a,b) = 1, sinon on pose a=ka' et b=kb' avec PGDC(a',b') = 1, dans ce cas-là, la démonstration ci-dessous portera sur a' et b'. On a d'après le début de la démonstration de Marjani:  Donc avec :  Donc soit d=1 ou d=2 Cas numéro 1 : c est pair, donc c+1 et c-1 sont impairs, ce qui donne d=1 La fraction :  est donc irréductible, et elle est égal à a²/b², donc : c+1 =a² et c-1=b² Ce qui donne a²-b²=2 <=> (a-b)(a+b)=2 donc a-b=1 et a+b=2 => 2a=3 contradiction. Cas numéro 2 : c est impair, donc c+1 et c-1 sont pairs, ce qui donne : d=2 On pose c=2k+1, on trouve que :  Tel que la fraction k+1/k est irréductible (PGDC(k+1,k)=1) Donc k+1=a² et k=b², ce qui donne a²-b²=1, donc (a-b)(a+b)=1 => a-b=1 et a+b=1 => a=1 et b=0, contradiction avec b non nul. Dans les deux cas, on tombe sur une contradiction. Ce qui prouve que l'hypothèse est érronée : la fraction donnée n'est pas un entier. | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Sam 04 Sep 2010, 00:02 Sam 04 Sep 2010, 00:02 | |
| Très pertinente ta remarque.. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Sam 04 Sep 2010, 00:35 Sam 04 Sep 2010, 00:35 | |
|
Dernière édition par M.Marjani le Sam 04 Sep 2010, 00:39, édité 1 fois | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Sam 04 Sep 2010, 00:37 Sam 04 Sep 2010, 00:37 | |
| - M.Marjani a écrit:
- oussama1305 a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- Un exercice de plus:
Soient a et b deux entiers naturels non nuls, tel que a>b.
Démontrez que 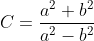 n'est pas un entier. n'est pas un entier.
Bonne chance.
Ma Solution:
+b^2\left ( 1+c \right )=0\Leftrightarrow \frac{c+1}{c-1}=(\frac{a}{b})^2)
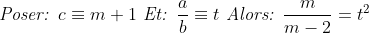
m et m-2 ne peuvent pas étre deux carrés en méme temps Car: 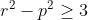 Pour tout Pour tout \varepsilon \mathbb{N})
Donc il n'existe pas de couple solution pour l'équation du départ. D'ou 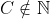
Je ne parle pas de ce cas-là, mais deux nombres peuvent ne pas être des carrés, mais leur fraction, oui; Et j'insiste sur "pas ce cas-là". Par exemple 18 et 2 ne sont pas des carrés, mais 18/2 = 9 = 3² oui.
Une autre méthode pour résoudre l'exercice.
Supposons que la fraction est vraiment un entier c, et supposons que PGDC(a,b) = 1, sinon on pose a=ka' et b=kb' avec PGDC(a',b') = 1, dans ce cas-là, la démonstration ci-dessous portera sur a' et b'.
On a d'après le début de la démonstration de Marjani:

Donc avec :

Donc soit d=1 ou d=2
Cas numéro 1 : c est pair, donc c+1 et c-1 sont impairs, ce qui donne d=1
La fraction :  est donc irréductible, et elle est égal à a²/b², donc : c+1 =a² et c-1=b² est donc irréductible, et elle est égal à a²/b², donc : c+1 =a² et c-1=b²
Ce qui donne a²-b²=2 <=> (a-b)(a+b)=2 donc a-b=1 et a+b=2 => 2a=3 contradiction.
Cas numéro 2 : c est impair, donc c+1 et c-1 sont pairs, ce qui donne : d=2
On pose c=2k+1, on trouve que :

Tel que la fraction k+1/k est irréductible (PGDC(k+1,k)=1)
Donc k+1=a² et k=b², ce qui donne a²-b²=1, donc (a-b)(a+b)=1 => a-b=1 et a+b=1 => a=1 et b=0, contradiction avec b non nul.
Dans les deux cas, on tombe sur une contradiction.
Ce qui prouve que l'hypothèse est érronée : la fraction donnée n'est pas un entier.
J'ai pas lu... Mais m/(m-2) est un entier si et si que m=3 ou m=4 dans les deux cas, ils ne donnent pas de carré.
A trés bientot ^^ Il faut que tu le fasses parce que comme a dit Othman c'est une remarque très pertinente et qui va surement t'aider dans d'autres exercices  | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Sam 04 Sep 2010, 00:43 Sam 04 Sep 2010, 00:43 | |
| Si je peux me permettre, quelle remarque au juste? | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Sam 04 Sep 2010, 00:47 Sam 04 Sep 2010, 00:47 | |
| - Citation :
- Je ne parle pas de ce cas-là, mais deux nombres peuvent ne pas être des carrés, mais leur fraction, oui; Et j'insiste sur "pas ce cas-là". Par exemple 18 et 2 ne sont pas des carrés, mais 18/2 = 9 = 3² oui.
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  Sam 04 Sep 2010, 00:48 Sam 04 Sep 2010, 00:48 | |
| - oussama1305 a écrit:
- Si je peux me permettre, quelle remarque au juste?
La méme question que je veux savoir aprés lire ce qui suit du methode de Oussama. EDIT: - Othmann a écrit:
- Je ne parle pas de ce cas-là, mais deux nombres peuvent ne pas être des carrés, mais leur fraction, oui; Et j'insiste sur "pas ce cas-là". Par exemple 18 et 2 ne sont pas des carrés, mais 18/2 = 9 = 3² oui.
Merçi de lire: - M.Marjani a écrit:
- m/(m-2) est un entier si et si que m=3 ou m=4 dans les deux cas, m/(m-2) ne donne pas de carré.
A trés bientot ^^ | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Arithmétiques et raisonnement par absurde: Sujet: Re: Arithmétiques et raisonnement par absurde:  | |
| |
|
  | |
| | Arithmétiques et raisonnement par absurde: |  |
|
