modeste!

soit a,b et c des réels tels que: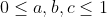,Prouver que:

(crée par moi)

On a :

Il suffit de prouver que :


Ce qui est vrai ..
Avec égalité ssi a=b=c=1

T'as commis une error Mr Sylphaen, dans la deuxiéme ligne, il faut dire plutot que: abc+2>=a+b+c <=> a(bc-1)+2-(b+c)>=0
Cela rend tout est faux je pense.

Wé bien vu .. C'étais une faute de signe !
On peut réécrire l'inégalité ainsi :

CQFD..

Ok, bien joué, maintenant on est d'accord .

J'ai pas bien compris ce que tu veux dire parce ce que :
a(bc-1)+2-(b+c)=a(bc-1)+1-bc + (bc+1 -b-c)
=(1-bc)(1-a)+(1-b)(1-c)
Puis que a et b et c sont <= 1 alors la somme est positive !

oui, car si on a :
a=b=c=1
on trouve que:
3/2<=3/2