Géométrie

Soit ABC un triangle dans lequelle AC=max{AB,BC,CA}. Soit O son centre du cercle circonscrit, N un point de AC, les médiatrices de CN et AN coupe BC et AB en en M et K, Prouver que O, M, K et B sont cocyclique.

Expert sup Nombre de messages : 1482 Age : 30 Date d'inscription : 12/12/2009

M, K et B sont colinéaires. Comment se peut-il que O,M,K et B soient cocycliques ?

Dijkschneier a écrit:: M, K et B sont colinéaires. Comment se peut-il que O,M,K et B soient cocycliques ?

Je ne crois pas que M, K, B sont collinéaires, quelque chose n'est pas correcte dans ton diagrame, sinon dans mon ennoncé, si tu trouve toujours que M,K et B sont collinéares, essaye de faire une figure avec geogebra et poste la dans ce topic, on rectifiera l'ennoncé si c'est necessaire.

Sujet: Re: Géométrie Dim 02 Jan 2011, 15:43

L'exercice est juste et les points sont bels et bien cocylciques.
Je visn de finir la solution je la posterais après Very Happy

Sujet: Re: Géométrie Dim 02 Jan 2011, 16:02

Voilà nous devons prouver que <OBM=<OKM
Posons F le milieu de [AN] et E le milieu de [CN]
Nous avons <OKM=180°-<MKB-<OKA=180°-<BAC-<BCA+180°-<KMC-<CKF-<FKA=360°<CKF-<FKA-(<BAC+<BCA+KMC)
et puisque les triangles AKF et KCF sont rectangles donc
<OKM=<KCF+90°+<BAC+90-<BCA-<BAC-KMC=<BCA-<MCK=<MCK
Donc le triangle MCK est isocèle et puisuqe O est le cercle circonscrit de ABC donc OBC est isocèle
Il s'ensuit que les deux triangles OBC et MKC sont semblables donc
<OKM=<OCM=<OBM
donc les points O,M,K et B sont cocycliques
CQFD Very Happy

Sujet: Re: Géométrie Dim 20 Mar 2011, 14:23

Salut Mehdi.O!
Belle tentative mais tu as du commettre une erreure quelque part, car le triangle MCK n'est pas forcément isocèle comme tu verra dans ma figure. Depuis Août, ce problème est sans solution, je me permet donc de proposer ma solution dédiée à ceux que y voient intêret.
Solution.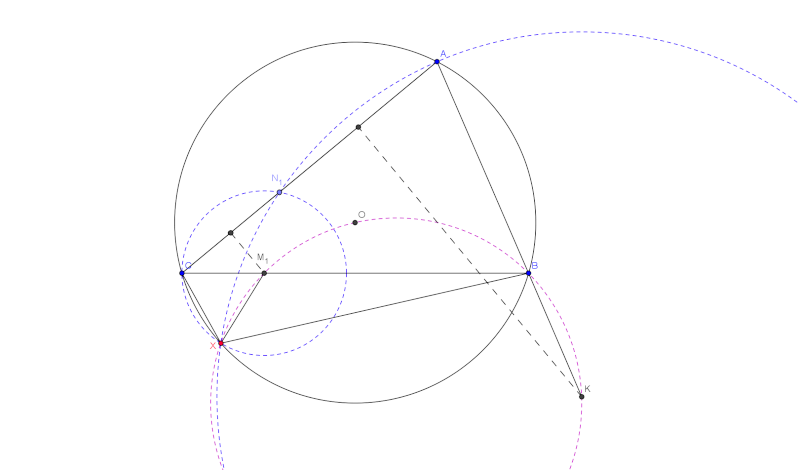
Géométrie Attach15

Soit M_1 et X les points d'intersection du cercle circonscrit au triangle KBO avec BC et le cercle circonscrit au triangle ABC respectivement.
On a: 2angle{M_1CX}=angle{XOB}=angle{XM_1B} d'où M_1C=M_1X. De même, on a: 2angle{XAK}=angle{XOB}=180°-angle{XKA} d'où KA=KX. Soit N_1 le point d'intersection des cercles C_1(K,KA) et C_2(M_1,M_1C) autre que X. On remarque que: angle{CN_1X}+angle{XN_1A}=180° et donc N_1£AC ainsi N_1=N et par conséquent M_1=M. Il s'ensuit directement que K,B,O et M sont cocycliques.

Sujet: Re: Géométrie Dim 20 Mar 2011, 17:29

j'arrive pas à comprendre pourquoi :
angle{CN_1X}+angle{XN_1A}=180°
Et merci d'avance de ta réponse .

Sujet: Re: Géométrie Dim 20 Mar 2011, 18:23

Avec plaisir.
On a: 2angle{CN_1X}=angle{CM_1X}=angle{XKA} et 2angle{XN_1A}=360°-angle{XKA}, en sommant les deux on trouve que: angle{CN_1X}+angle{XN_1A}=180°.
J'espère que c'est claire maintenant.

Sujet: Re: Géométrie Dim 20 Mar 2011, 19:01

Clair comme l'eau de source thx Smile

et joli solution .

» exo de geometrie
» Géométrie
» géométrie (4+)
» géométrie
» la geometrie