Considérons l'équation du troisième degré d'inconnue x
: x^3+3x²+15x-99=0)
.
Forme réduite:Trouvez trois nombres réels a, p, et q tels que pour tout réel x, on ait:
^3+p(x+a)+q)
.
On ppose alors
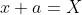
et on résout "l'équation réduite"
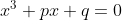
.
où a, p, et q ont les valeurs trouvées.
Cette façon de "réduire" l'équation a été éxposé par Viète, Cadran, et Descartes.
Dites-le avec un vers, un peu d'histoire avec Tartaglia:Nicolo Tartaglia (Mathématicien italien du 16-ème siècle) a dévoilé à Cadran, dans un poème comment il résolvait l'équation
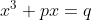
. (avec p et q positifs).
"Lorsque le cube et les choses à côté
S'égalent à quelque nombre discret:
Trouves-en deux, espacés du connu,
Et fais en sorte, suivant l'us,
Que leurs produit toujours égale
Le tiers cubé des choses, net.
Et le résidu général
Des côtés cubes bien soustraits
Te donnera ta chose principale."
Nous dirions aujourd'hui: pour résoudre l'équation:
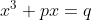
, trouvez deux nombres u et v tels que:
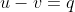
et
^3)
.
Alors une solution est:

.
Nous ne ferons pas comme Tartaglia, nous allons voir une autre methode.
La methode éxposé par Hudde (17-ème siècle):Pour résoudre l'équation
: x^3+12x-112=0)
, Hudde propose de poser
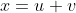
a/ Vérifiez que
^3=u^3+v^3+3uv(u+v))
.
Déduisez en lorsque
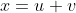
, on a:
(u+v)-112)
;
et que
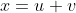
est solution de
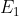
lorsque:
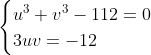
soit
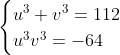
.
b/ On peut trouver deux nombres u et v tels que
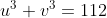
et
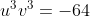
. Pourquoi? Quels sont ces nombres?
c/Calculez alors une solution
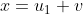
de
)
, puis résolvez l'équation
)
.
Indication: vérifiez que
^3=56+40\sqrt{2})
.
d/Résolvez l'équation

donnée initialement.
La fameuse methode de Cardan:A voir ici: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Cardan.
P.S: le livre d'où j'ai tiré ces methode ne parle pas de la methode de Cardan, car il s'agit d'un livre de Première S.
Les démarches présentés ici peuvent être généralisé.
