| | A=.... |  |
|
+4Mehdi.O M.Marjani Dijkschneier yumi 8 participants |
|
| Auteur | Message |
|---|
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: A=.... Sujet: A=....  Ven 08 Oct 2010, 18:55 Ven 08 Oct 2010, 18:55 | |
| salam all
حدد بتفصيل المجموعة التالية
A={(x,y}E Z² ;x²+xy-2y+5=0}
qui peut m'expliquer la question d'abord ?
est ce que normalement on doit trouver les couples x et y pour lesquels l'équation x²+xy-2y+5=0 reste juste?
si c ça alors moi j trouver les couples (1,2);(-1;-2);(3,-2);(-3;2)
Dernière édition par yumi le Sam 09 Oct 2010, 23:19, édité 2 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Ven 08 Oct 2010, 21:12 Ven 08 Oct 2010, 21:12 | |
| - yumi a écrit:
- salam all
[b]
حدد بتفصيل المجموعة التالية
A={(x,y}E Z² ;x²+xy-2y+5=0}
qui peut m'expliquer la quetsion d'abord svp ?
est ce que normalement on doit trouver les couples x et y pour lesquels l'équation x²+xy-2y+5=0 reste juste?
C'est à peu près ça. Il s'agit de trouver les couples (x,y) appartenant à Z² et vérifiant : x²+xy-2y+5=0. - yumi a écrit:
si c ça alors moi j trouver deux couples (2;3),(-2;-3)
Non. Les deux couples que tu proposes ne marchent pas. Solution :Soit (x,y) de A. Alors x et y sont deux entiers relatifs vérifiant : x²+xy-2y²+5=0. Si x était pair, alors x²+xy-2y²+5 serait impair, et ne pourrait donc pas être nul. Ainsi, x est impair. Si maintenant y était pair, alors x²+xy-2y²+5 serait impair, et ne pourrait donc pas être nul. Ainsi, x est impair tandis que y est pair. Par conséquent : %20\in%20\mathbb{Z}^2%20:%20x=2x%27+1%20\%20et%20\%20y=2y%27) ^2+(2x%27+1)2y%27-2(2y%27)^2+5%20\\%20&=%202(x%27(x%27+1)+y%27(2x%27+1)-4y%27^2+3)%20\end{align*}) Par suite, +y%27(2x%27+1)-4y%27^2+3=0) On sait par ailleurs que x'(x'+1) est pair. Et la somme étant nulle, donc paire, on a nécessairement que y'(2x'+1) est impair, c'est-à-dire que y' est impair. Par conséquent : ) Considérons maintenant l'équation x²+xy-2y²+5=0 d'inconnue x et de paramètre y. %20\\%20&=%209y^2-20%20\end{align*}) 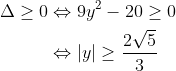 Si 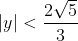 , alors l'équation n'aurait pas de solution, et le couple (x,y) n'existerait pas. Ainsi, 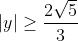 . Par conséquent, 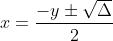 . Et puisque on a établi que ) , alors )^2-20%20=%204(9(2y%27%27+1)^2-5)) . Par suite, \pm%20\sqrt{(3(2y%27%27+1))^2-5}) . Et puisque x est un entier relatif, alors )^2-5}) est un entier naturel. Et on sait que 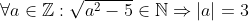 . Donc |3(2y''+1)|=3, c'est-à-dire que y''=0 ou y''=-1. On en déduit que y=2(2y''+1) 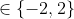 , et que 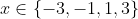 . Inversement, les couples (3,-2), (-1,-2), (1,2) et (-3,2) appartiennent à A. Donc A = {(3,-2), (-1,-2), (1,2), (-3,2)}.
Dernière édition par Dijkschneier le Sam 09 Oct 2010, 23:01, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 20:18 Sam 09 Oct 2010, 20:18 | |
| Comment ça:
"alors moi j trouver deux couples (2;3),(-2;-3)"
"Inversement, les couples (1,2) et (-3,2) appartiennent à A.
Donc A = {(1,2),(-3,2)}."
?!
Non, mais ç'est impossible ! Car: x²+xy-2y+5=0 <=> y(-x+2)=x²+5 >= 5
Puisque y(2-x) > 0 donc il y aurait deux cas, le cas ou y>0 et 2>x , le cas ou y<0 et x>2 (1)
Ce qui rend les 2 solutions de Yumi impossibles, et une solution de Dijkschneier. (-3,2) aussi n'est pas un couple solution en remplaçant.
On suppose par l'absurde que x=2 est une solution, donc x²+xy-2y+5=0 => 4+2y-2y+5=0 ==> Absurde.
D'ou x=/2. Alors on peut dire maintenant que: y=(x²+5)/(2-x)
On peut voir que (x²+5)/(2-x) >= 2 <=> x²+5-4+2x >= 0 <=> (x+1)² >= 0 ce qui est vrai ! Donc y>=2 ce qui rend x<2 d'aprés (1)
Jusqu'à maintenant on peut inspirer de y=(x²+5)/(2-x) (avec y=2) que S_1={-1,2}
On peut voir également que y=(x²+5)/(2-x) £ IN*-{1,2} (2 annuler car on l'a trouvé)
Dernière édition par M.Marjani le Sam 09 Oct 2010, 20:57, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 20:51 Sam 09 Oct 2010, 20:51 | |
| Il y a eu quiproquo. C'est soit qu'on parle de x²+xy-2y²+5=0 ou bien de x²+xy-2y+5=0.
J'ai travaillé, en ce qui me concerne, sur la première, et cela me semble l'essence du problème. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 21:00 Sam 09 Oct 2010, 21:00 | |
| - Dijkschneier a écrit:
- Il y a eu quiproquo. C'est soit qu'on parle de x²+xy-2y²+5=0 ou bien de x²+xy-2y+5=0.
J'ai travaillé, en ce qui me concerne, sur la première, et cela me semble l'essence du problème. Ahoui. C'est bien ton effort en tout cas de travailler sur x²+xy-2y²+5=0. On la considére une solution d'un probléme. | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 21:56 Sam 09 Oct 2010, 21:56 | |
| salam
bah moi voilà ce que j fait
x²+xy-2y²=(x-y)(x+2y)=-5
donc [(x-y)=-5 et (x+2y)=1]ou[(x-y)=-1 et (x+2y)=5]ou....
lmohim ya 4 cas
enfin on aura
A={(1,2);(-1;-2);(3,-2);(-3;2)}
j'attends vos confirmations...
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 22:28 Sam 09 Oct 2010, 22:28 | |
| C'est ça Yumi uen simple factorisation et le coup est joué ... Pas la peine d'aller plus loin  ! | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 22:38 Sam 09 Oct 2010, 22:38 | |
| wé merci mehdio  | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 23:24 Sam 09 Oct 2010, 23:24 | |
| et au fait oui t'as raison dijkshneier c pas 2 couples mais 4
c seulement que je me suis trompée dans le calcul voilà j corrigé dans l'énoncé
merci pr vos réponses
bonne nuit à vous tous
salam | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Sam 09 Oct 2010, 23:38 Sam 09 Oct 2010, 23:38 | |
| - yumi a écrit:
- et au fait oui t'as raison dijkshneier c pas 2 couples mais 4
c seulement que je me suis trompée dans le calcul voilà j corrigé dans l'énoncé
merci pr vos réponses
bonne nuit à vous tous
salam Il faut corriger A={(x,y}E Z² ;x²+xy-2y+5=0} plutot ... | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 06:59 Dim 10 Oct 2010, 06:59 | |
|
salam
je ne vois pas dans l'énoncé que x ,y E Z²
-------------------------
dans IR²: il s'agit (x,y) coord de points M appartenant à la réunion de 2 courbes.
-2y² + xy + x²-5 = 0
delta= 9x²-4 ===> |x|>= 4/9
y' = (x+V(9x²-4))/4 et y" = (x-V(9x²-4))/4
________________
| |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 08:12 Dim 10 Oct 2010, 08:12 | |
| bah voilà l'énoncé
حدد بتفصيل المجموعة التالية
A={(x,y}E Z² ; x²+xy-2y+5=0}
donc (x;y) E Z².....
et pr Houssa et Marjani j'arrive pas à comprendre ce que vous voulez dire,pouvez vous vous expliquez ?? | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 10:27 Dim 10 Oct 2010, 10:27 | |
| salam
mes excuses , je n'ai pas fait attention
donc je propose
x² + xy -2y +5 =0 (équation du second degré en x)
deltaD = y² +8y -24 = (y+4)²-36 = doit être un carré parfait = a²
===> (y+4)²-a² = 36
===> (y+4+a)(y+4-a) = 36
===> des systèmes en y et a ====> les valeurs de x
_______________________________________________
exemple1:
y+4+a=12
y+4-a = 3
===>2y +8 = 15 impossible
_________________________________
exemple 2:
y+4+a = 18
y+4-a=2
===> 2y+8=20 ====> y=6 ===> a =8
===> x'=(-y+a)/2 = 1 et x" = (-y-a)/2 = -7
_______________________ | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 10:55 Dim 10 Oct 2010, 10:55 | |
| Voilà une solution facile :
x²+xy-2y+5=0 donc (x-y)(x+2y)=5
et on sait que les diviseurs de 5 en Z sont 1,5 et -1,-5
à la fin on trouve 4 couples :
S={(1;2),(-1;-2);(3;-2);(-3;2)} | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 11:29 Dim 10 Oct 2010, 11:29 | |
| - yumi a écrit:
- bah voilà l'énoncé
حدد بتفصيل المجموعة التالية
A={(x,y}E Z² ; x²+xy-2y+5=0}
donc (x;y) E Z².....
et pr Houssa et Marjani j'arrive pas à comprendre ce que vous voulez dire,pouvez vous vous expliquez ?? Si c'est l'equation est ce qui est en rouge, donc vous avez trompez en croyant que x²+xy-2y²+5=0 . Je l'ai raisolu hier, si t'as besoin de la solution et si c'est la vrai énoncé qui est en rouge, je la posterai sans problémes. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 11:35 Dim 10 Oct 2010, 11:35 | |
| - Mehdi.O a écrit:
- Voilà une solution facile :
x²+xy-2y+5=0 donc (x-y)(x+2y)=5
et on sait que les diviseurs de 5 en Z sont 1,5 et -1,-5
à la fin on trouve 4 couples :
S={(1;2),(-1;-2);(3;-2);(-3;2)} La factorisation à laquelle tu procédé est erroné!En fait,Yumi a présenté 2 annoncés différents pour le problème ! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 12:01 Dim 10 Oct 2010, 12:01 | |
| - houssa a écrit:
- salam
mes excuses , je n'ai pas fait attention
donc je propose
x² + xy -2y +5 =0 (équation du second degré en x)
deltaD = y² +8y -24 = (y+4)²-36 = doit être un carré parfait = a²
===> (y+4)²-a² = 36
===> (y+4+a)(y+4-a) = 36
===> des systèmes en y et a ====> les valeurs de x
_______________________________________________
exemple1:
y+4+a=12
y+4-a = 3
===>2y +8 = 15 impossible
_________________________________
exemple 2:
y+4+a = 18
y+4-a=2
===> 2y+8=20 ====> y=6 ===> a =8
===> x'=(-y+a)/2 = 1 et x" = (-y-a)/2 = -7
_______________________ Bien ! De ma part j'ai trouvé à la fin que x=(y-V((y+4)²-36))/2 => (y-2x)²=(y+4)²-36 Avec y>=2 et x<2  Je pense que c'est la méme chose, et ce n'est pas la peine de répeter car la solution finale est: S={(-1,2),(1,6),(-7,6)} | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 16:39 Dim 10 Oct 2010, 16:39 | |
| Excusez moi mais ma factorisation est pour l'énoncé : x²+xy-2y²+5=0 | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 17:02 Dim 10 Oct 2010, 17:02 | |
| mais est ce qu'on peux pas utiliser la factorisation ?
x²+xy-2y+5=0 donc (x-y)(x+2y)=-5.....
sinon pk?? car avc la factorisation on trouve 4 couples et là Marjani t'as trouvé 3 couples....
qui peut mieux m''expliquer mieux car je me trouve perdue!!!??merci d'avance | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 22:04 Dim 10 Oct 2010, 22:04 | |
| - yumi a écrit:
- mais est ce qu'on peux pas utiliser la factorisation ?
x²+xy-2y+5=0 donc (x-y)(x+2y)=-5.....
sinon pk?? car avc la factorisation on trouve 4 couples et là Marjani t'as trouvé 3 couples....
qui peut mieux m''expliquer mieux car je me trouve perdue!!!??merci d'avance  x²+xy -2y+5=0 donc (x-y)(x+2y)=-5 ?! | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: A=.... Sujet: Re: A=....  Dim 10 Oct 2010, 22:09 Dim 10 Oct 2010, 22:09 | |
| ouais car si tu développes (x-y)(x+2y)+5=0 tu auras x²+xy-2y+5=0  sinon j'arrive pas à comprendre pk vous considérez ça faux??  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 | |
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 | |
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 | |
  | |
amazigh-tisffola
Expert grade1

 Nombre de messages : 487 Nombre de messages : 487
Age : 40
Localisation : kelaa m'gouna
Date d'inscription : 01/10/2010
 |  Sujet: Re: A=.... Sujet: Re: A=....  Lun 11 Oct 2010, 13:00 Lun 11 Oct 2010, 13:00 | |
| voici ma solution qui est classique,
x^2+xy-2y+5=0
x(x+y)-2y+5=0
x(x+y)-2y-2x+2x+5=0
x(x+y)-2(x+y)+2x+5=0
(x-2)(x+y)+2x+5=0
(x-2)(x+y)+2x-4+9=0
(x-2)(x+y+2)=-9
comme x et y sont dans Z alors x-2 et x+y+2 est dans Z,
==>x-2=1 et x+y+2=-9 ==>(3,-14)£A
x-2=3 et x+y+2=-3 ==>(5,-10)£A
x-2=9 et x+y+2=-1 ==>(11,-14)£A
x-2=-1 et x+y+2=9 ==>(1,6)£A
x-2=-3 et x+y+2=3 ==>(-1,2)£A
x-2=-9 et x+y+2=1 ==>(-7,6)£A
finalement on obtient A={(3,-14);(5,-10);(11,-14);(1,6);(-1,2);(-7,6)}
sauf erreur de ma part | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: A=.... Sujet: Re: A=....  | |
| |
|
  | |
| | A=.... |  |
|
