| | Epreuve d'olympiades . |  |
|
|
| Auteur | Message |
|---|
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Epreuve d'olympiades . Sujet: Epreuve d'olympiades .  Ven 15 Oct 2010, 14:22 Ven 15 Oct 2010, 14:22 | |
| Vu qu'on parle rarement des olympiades dans le forum ces derniers temps , je profite de ce temps libre pour vous proposer cette épreuve   P.S: Postez vos réponses ici  EDIT: longueurs pas longueur haha  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Ven 15 Oct 2010, 17:52 Ven 15 Oct 2010, 17:52 | |
| Merci tarask. Exercice 1 :1) Il s'agit de l'inégalité de Schur : la condition que a, b et c soient des longueurs de côté de triangle est inutile. 2) Équation polynomiale du troisième degré, donc trois solutions complexes d'après le théorème fondamental de l'algèbre. Supposons par l'absurde que cette équation possède une solution double, disons a. Celle-ci devrait être alors aussi une racine du polynôme dérivé de x^3 - x - 1, qui est 3x²-1, donc a devrait être à un signe près égal à sqrt(1/3). Mais sqrt(1/3) n'est pas une solution à l'équation x^3 - x - 1. Contradiction. Par conséquent, cette équation admet 3 solutions complexes différentes. De plus, en notant a, b et c ces racines complexes, on arrive à dire d'après les formules de Viète que : 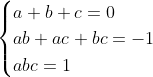 . Ainsi : %20\\%20&=%20-3%20+%202%20\cdot%20\frac{3+(ab+ac+bc)-2(a+b+c)}{1-(a+b+c)+(ab+ac+bc)-abc}%20\\%20&=%20-3%20+%202%20\cdot%20\frac{3-1-2\cdot%200}{1-0+(-1)-1}%20\\%20&=%20-3%20-%204%20\\%20&=%20-7%20\end{align*}) Exercice 2 : Exercice 2 :Sauf erreur de développement, l'inégalité présentée est équivalente à : x² + y² + 3 + 3(x+y) + xy + 2(sqrt(x)+sqrt(y)) + 2(xsqrt(x)+ysqrt(y))-4sqrt(xy) >= 0 Et c'est largement vrai : on peut voir par exemple que 3(x+y)-4sqrt(xy) = x+y +2(sqrt(x)-sqrt(y))² >= 0. Exercice 3 :(x²-2)(x²+7)(x²+14)=0 => x²-2 = 0 => |x| = sqrt(2). Et puisque sqrt(2) n'est pas un entier, alors cette équation n'a pas de solution dans IN. Je m'embrouille un peu dans la seconde partie : qu'est-ce qu'une solution modulo n ? | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Ven 15 Oct 2010, 19:19 Ven 15 Oct 2010, 19:19 | |
| pour le dérnier exo d'arith :
suppose P(x)=(x²-2)(x²+7)(x²+14) et N un entier t.q sa décomposition est N=(produit)p_i^alpha_i
il existe des entiers x_i t.q
P(x_1) = 0 (mod p1^alpha 1 )
P(x_2) = 0 (mod p2^alpha 2)
. .
. .
. .
P(x_n) = 0(mod pn^alpha n)
alors théo des chnois prouve l'existence d'un entier x tel que x=x_i (mod N)
d'ou P(x)=0 (mod N) a b1 une soluc
----------------------------------------------------------------------------------------------
ou on utilise la méthode classique su l'indicatrice d'uler (connu )
considérons p un nombre premier et prouvons avec le critére d'uler que 2,-7,-14 sont des carré mod p !
fermat ==> a^p-1 = 1(mod p) ==> (a^(p-1)/2-1)(a^(p-1)/2 +1 )=0 (mod p)
alors si on suppose que soit 2 soit -7 ne sont pas des carés mod p alors d'aprés critére d'uler ==> a^(p-1/2)=-1 (mod p )
pour a= 2 ==> 2^(p-1/2)=-1 (mod p )
pour a=-7 ===> -7^(p-1/2) =-1(mod p )
qui donnent ==< -14 ^(p-1/2) =1 (mod p )
alors -14 est un carrés mod p
pour exo 2 c'est b1 fait avec la formule de vieta ^^ !
exo 1 ; shur fera l'affaire
je posterais les autres solucs plus tard | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Ven 15 Oct 2010, 21:44 Ven 15 Oct 2010, 21:44 | |
| Bonsoir  Merci d'abord pour votre intérêt  - Dijkschneier a écrit:
- Merci tarask.
Exercice 1 :
1) Il s'agit de l'inégalité de Schur : la condition que a, b et c soient des longueurs de côté de triangle est inutile.
2) Équation polynomiale du troisième degré, donc trois solutions complexes d'après le théorème fondamental de l'algèbre.
Supposons par l'absurde que cette équation possède une solution double, disons a. Celle-ci devrait être alors aussi une racine du polynôme dérivé de x^3 - x - 1, qui est 3x²-1, donc a devrait être à un signe près égal à sqrt(1/3). Mais sqrt(1/3) n'est pas une solution à l'équation x^3 - x - 1. Contradiction.
Par conséquent, cette équation admet 3 solutions complexes différentes.
De plus, en notant a, b et c ces racines complexes, on arrive à dire d'après les formules de Viète que :
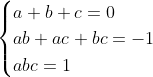 . .
Ainsi :
%20\\%20&=%20-3%20+%202%20\cdot%20\frac{3+(ab+ac+bc)-2(a+b+c)}{1-(a+b+c)+(ab+ac+bc)-abc}%20\\%20&=%20-3%20+%202%20\cdot%20\frac{3-1-2\cdot%200}{1-0+(-1)-1}%20\\%20&=%20-3%20-%204%20\\%20&=%20-7%20\end{align*})
Exercice 2 :
Sauf erreur de développement, l'inégalité présentée est équivalente à :
x² + y² + 3 + 3(x+y) + xy + 2(sqrt(x)+sqrt(y)) + 2(xsqrt(x)+ysqrt(y))-4sqrt(xy) >= 0
Et c'est largement vrai : on peut voir par exemple que 3(x+y)-4sqrt(xy) = x+y +2(sqrt(x)-sqrt(y))² >= 0.
Exercice 3 :
(x²-2)(x²+7)(x²+14)=0 => x²-2 = 0 => |x| = sqrt(2). Et puisque sqrt(2) n'est pas un entier, alors cette équation n'a pas de solution dans IN.
Je m'embrouille un peu dans la seconde partie : qu'est-ce qu'une solution modulo n ? Tes idées sont très bonnes je t'en félicite  Pour l'exercice 2 , à mon avis , développer sera une torture  J'ai pas essayé cette voie ..... Je vais poster une solution officielle après d'autres interventions. En tout cas voilà la clé en spoiler : - Spoiler:
savoir que :  puis utiliser AM-HM 
- master a écrit:
- pour le dérnier exo d'arith :
suppose P(x)=(x²-2)(x²+7)(x²+14) et N un entier t.q sa décomposition est N=(produit)p_i^alpha_i
il existe des entiers x_i t.q
P(x_1) = 0 (mod p1^alpha 1 )
P(x_2) = 0 (mod p2^alpha 2)
. .
. .
. .
P(x_n) = 0(mod pn^alpha n)
alors théo des chnois prouve l'existence d'un entier x tel que x=x_i (mod N)
d'ou P(x)=0 (mod N) a b1 une soluc
----------------------------------------------------------------------------------------------
ou on utilise la méthode classique su l'indicatrice d'uler (connu )
considérons p un nombre premier et prouvons avec le critére d'uler que 2,-7,-14 sont des carré mod p !
fermat ==> a^p-1 = 1(mod p) ==> (a^(p-1)/2-1)(a^(p-1)/2 +1 )=0 (mod p)
alors si on suppose que soit 2 soit -7 ne sont pas des carés mod p alors d'aprés critére d'uler ==> a^(p-1/2)=-1 (mod p )
pour a= 2 ==> 2^(p-1/2)=-1 (mod p )
pour a=-7 ===> -7^(p-1/2) =-1(mod p )
qui donnent ==< -14 ^(p-1/2) =1 (mod p )
alors -14 est un carrés mod p
pour exo 2 c'est b1 fait avec la formule de vieta ^^ !
exo 1 ; shur fera l'affaire
je posterais les autres solucs plus tard très jolie ta réponse pour l'exercice d'arithmétique  P.S: j'espère qu'il y aura d'autres initiatives  Et merci pour votre intérêt encore une fois  | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Ven 15 Oct 2010, 22:05 Ven 15 Oct 2010, 22:05 | |
| exo 2 :
b1 vu que (2+x+y)²>=2(1+x)(1+y) <==>2+x+y/(1+x)(1+y) >= 2/x+y+2
<==> 1/1+x + 1/1+y >= 2/x+y+2 <==> 1/2(1/1+x + 1/1+y) >=1/x+y+2
ce qui est vrais car 1+x>=2Vx ==> 2(1+x)>=(1+Vx)² | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Sam 16 Oct 2010, 13:06 Sam 16 Oct 2010, 13:06 | |
| Quelqu'un peut-il préciser le sens d'une solution modulo n ?  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Dim 17 Oct 2010, 21:39 Dim 17 Oct 2010, 21:39 | |
| - Dijkschneier a écrit:
- Quelqu'un peut-il préciser le sens d'une solution modulo n ?
 Bonsoir Dijkschneier  D'abord , je précise que c'est un exercice tiré du cours d'animath  (voir page 61  ) Bon , pour l'équation : Je vois bien de quoi tu parles : qu'est-ce qu'il a ce modulo N à faire ici ?  Moi aussi je n'avais pas bien compris cet exercice , j'ai au début songé aux complexes ... pas du tout une bonne idée  J'avais beaucoup cherché avant de proposer le test , et voilà quelques lien qui m'ont vraiment clarifié quelque chose : les résidus quadratiques !! http://www.acrypta.com/telechargements/fichecrypto_210.pdf http://www.acrypta.com/telechargements/fichecrypto_200.pdf Bonne lecture Dijkschneier et désolé pour le retard  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Dim 17 Oct 2010, 22:12 Dim 17 Oct 2010, 22:12 | |
| Bah... Les résidus quadratiques modulo n, je comprends bel et bien. Une solution modulo n, je ne vois pas encore ce que ça peut signifier  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Dim 17 Oct 2010, 22:50 Dim 17 Oct 2010, 22:50 | |
| - Dijkschneier a écrit:
- Bah...
Les résidus quadratiques modulo n, je comprends bel et bien. Une solution modulo n, je ne vois pas encore ce que ça peut signifier  A vrai dire , ça me parait étrange moi aussi !!! j'ai confirmé la réponse de master (la deuxième, je précise !! ) parce qu'elle était semblable (plus ou moins) à l'officielle(à la manière des mauvais correcteurs)  J'ai lu les deux pdfs que je t'ai filés ..... ça a commencé à s'éclaircir .... quand tout à cas ça donne plus aucun sens  P.S: Je crois que seul un étudiant au sup pourra nous expliquer celà  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 18 Oct 2010, 19:20 Lun 18 Oct 2010, 19:20 | |
| D'accord tarask.
Quelqu'un peut-il préciser le cas d'égalité (s'il existe) pour l'inégalité proposée dans l'exercice 2 histoire de vérifier mon développement ? | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 | |
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 18 Oct 2010, 21:28 Lun 18 Oct 2010, 21:28 | |
| | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 20:00 Lun 06 Déc 2010, 20:00 | |
| | |
|
  | |
Nettah108
Féru
 Nombre de messages : 35 Nombre de messages : 35
Age : 30
Localisation : Larache
Date d'inscription : 11/11/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 21:58 Lun 06 Déc 2010, 21:58 | |
| bah on dit en arithmétique que a est congru à b modulo n si et seulement si n divise a-b  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 22:44 Lun 06 Déc 2010, 22:44 | |
| - Nettah108 a écrit:
- bah on dit en arithmétique que a est congru à b modulo n si et seulement si n divise a-b
 C'est vrai ?? ça veut dire que je connais rien à l'arithmétique ! Non , mais s'il te plait , essaye de lire tout le sujet !!! | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 22:51 Lun 06 Déc 2010, 22:51 | |
| Une solution modulo N , ne serait-ce pas un nombre qui vérifie que l'équation est juste pour chaque anneau quotient , on dois alors montrer que ce ne nombre existe (en faite ça vas être une famille de nombres congru à un même nombre modulo N) et je pense que cette famille vas changé d'anneau en anneau ce qui est logique , mais la question demande de montrer seulement qu'elle existe quelque soit L'anneau ... En espérant ne pas m'être gouré :p | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 22:55 Lun 06 Déc 2010, 22:55 | |
| Généralement un polynôme à coefficients entiers admet une racine modulo un nombre entier p si et seulement si:
il existe un entier x tel que p divise P(x)
On utilise la relation de congruence modulo un nombre n (notée par les trois tirés superposés et puis le nombre n est à droite indiqué, je la noterais par '=') définie par a=b (mod n) si et seulement si: n divise a-b
En particulier P admet une racine modulo n si il existe un entier x tel que : P(x)=0 (mod n)
Pourquoi définir la relation de congruence?
La réponse est simple: car cette relation est compatible avec l'addition et la multiplication càd:
si a=b (mod n) et a'=b' (mod n) alors a+a'=b+b' (mod n) et aa'= bb' (mod n)
On a en particulier a^k=b^k (mod n ) pour tout k ( peut etre facilement montré par récurrence)
Des applications de tout ça ?
bah il y en a pleiiiin!!!
par exemple: montrer que 2^2010-1 est dévisible par 3
Réponse: ona 2=-1 (mod 3)
Donc 2^2010=(-1)^2010=1 (mod3) d'ou 3 divise 2^2010-1
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 23:16 Lun 06 Déc 2010, 23:16 | |
| Bonsoir darkpseudo et supista !! Premièrement merci pour votre intérêt . @darkpseudo : que veux tu dire par une famille au juste ?? J'ai bien saisi ton idée , toutefois , je trouve du mal à faire un lien entre l'exercice et tes propos (peut-être qu'il n'y a pas de lien..) @supista: Les propriétés que vous avez citées , je les maîtrise bien , mais revenons à notre exercice : l'équation admet √2 et -√2 comme solutions dans R , d'après l'énoncé , pour tout entier N l'équation admet une solution modulo cet entier ....  comment ça se peut ???? | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 23:34 Lun 06 Déc 2010, 23:34 | |
| ok Tarask, je vais répondre à ta question:
ça parait bizarre un peu, mais cela est vrais prenons par exemple P=X^2-2
P admet une racine modulo 7 , en effet si tu prends X=3
Généralement pour un nombre premier p >2 on a le critère suivant :
P=X^2-2 admet une racine modulo p si et seulement si p^2-1 est divisible par 16 (Euler)
Donc P admet des racines pour tout entier premier p vérifiant le critère
Donc une équation peut ne pas avoir de solution dans N mais admet des solution modulo un entier.
De plus pour Q=X^2+2 qui n'admet pas de solution dans R admet 3 pour solution modulo 11
je peux aller meme plus loin, R=X^2+1 admet des racice modulo tout nombre premier p qui s'ecrit sous la forme 4k-1 ( et il y en a une infinité...)
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 23:53 Lun 06 Déc 2010, 23:53 | |
| - supista a écrit:
- ok Tarask, je vais répondre à ta question:
ça parait bizarre un peu, mais cela est vrais prenons par exemple P=X^2-2
P admet une racine modulo 7 , en effet si tu prends X=3
Généralement pour un nombre premier p >2 on a le critère suivant :
P=X^2-2 admet une racine modulo p si et seulement si p^2-1 est divisible par 16 (Euler)
Donc P admet des racines pour tout entier premier p vérifiant le critère
Donc une équation peut ne pas avoir de solution dans N mais admet des solution modulo un entier.
De plus pour Q=X^2+2 qui n'admet pas de solution dans R admet 3 pour solution modulo 11
je peux aller meme plus loin, R=X^2+1 admet des racice modulo tout nombre premier p qui s'ecrit sous la forme 4k-1 ( et il y en a une infinité...)
Rouge : pourquoi ? (je sais que c'est le critère d'Euler , mais je vois pas d'où vient le 16 ) Désolé si je pose trop de questions (c'est minuit  ) P.S: maintenant je commence à le comprendre cet exercice . | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Lun 06 Déc 2010, 23:56 Lun 06 Déc 2010, 23:56 | |
| Au fait mon idée est un peu là même que celle de supista , même si certain de ces propos restes un peu flou à mes yeux . Mais ce que je veux dire par une famille :
par exemple si l'equation admet une solution par exemple pour l'anneau quotient de deux l'equation devien :
x^2(x^2+1)*x^2 =0 il est clair que dans ce cas 0 est une solution
Donc on peut dire que tout les nombre pair vérifient l'équation modulo 2 ( en d'autre termes si on remplace un nombre pair dans l'equation on verra qu'il est congru à 0 modulo 2 )
Maintenant reste à montré ça pour tout les N | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Mar 07 Déc 2010, 01:06 Mar 07 Déc 2010, 01:06 | |
| non ça fait plaisir de te répondre  il y a deux critère de gauss dans la théorie des résidus quadratique, l'un de ces critères dis que 2 est résidu quadratique modulo un nombre premier impaire p si et seulement si (p^2-1)/8 est pair | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Mar 07 Déc 2010, 13:40 Mar 07 Déc 2010, 13:40 | |
| Bonjour . Merci supista d'avoir pris la peine de répondre , maintenant j'ai bien compris l'exercice. Merci à toi aussi drakpseudo  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  Mar 07 Déc 2010, 14:13 Mar 07 Déc 2010, 14:13 | |
| Je crois que ce qui est à retenir est cela : - supista a écrit:
- En particulier P admet une racine modulo n si il existe un entier x tel que : P(x)=0 (mod n)
Ainsi, dans un langage différent, le problème 3 peut se traduire en : "Montrer que pour tout entier N, il existe deux entiers x et k tels que : (x²-2)(x²+7)(x²+14)=kN." | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Epreuve d'olympiades . Sujet: Re: Epreuve d'olympiades .  | |
| |
|
  | |
| | Epreuve d'olympiades . |  |
|
