| | Inégalités |  |
|
+4nmo louis Dijkschneier Azerty1995 8 participants |
| Auteur | Message |
|---|
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Inégalités Sujet: Inégalités  Lun 24 Jan 2011, 14:18 Lun 24 Jan 2011, 14:18 | |
| Salut, Exercice 1Soit x un réel strictement positif tel que: 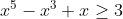 Montrez que: 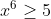 Exercice 2 Exercice 2Soit a,b,c trois réels strictement positifs tel que: 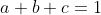 Montrez que : 1) 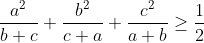 2) ^{2}}{c+1}+\frac{(b+c)^{2}}{a+1}+\frac{(c+a)^{2}}{b+1}\geq 1) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Lun 24 Jan 2011, 14:58 Lun 24 Jan 2011, 14:58 | |
| Pour le premier, la première étape est de multiplier les deux côtés par x², et d'avoir ainsi les deux relations :
x^5 - x^3 + x >= 3
x^7 - x^5 + x^3 >= 3x²
...
Le second se fait en une seule ligne avec Cauchy-Schwarz. | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Lun 24 Jan 2011, 15:31 Lun 24 Jan 2011, 15:31 | |
| On a 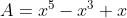 Donc x^2) Donc 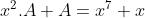 Donc =x^7+x) Donc 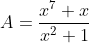 Donc A) Et puisque 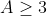 Donc ) Et on a pour tous réels positifs 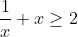 Donc 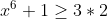 Donc 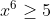 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Lun 24 Jan 2011, 18:28 Lun 24 Jan 2011, 18:28 | |
| - Dijkschneier a écrit:
- Pour le premier, la première étape est de multiplier les deux côtés par x², et d'avoir ainsi les deux relations :
x^5 - x^3 + x >= 3
x^7 - x^5 + x^3 >= 3x²
... Je ne peux pas savoir ton prochain pas, tu peux détailler. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Lun 24 Jan 2011, 18:39 Lun 24 Jan 2011, 18:39 | |
| Le prochain pas est de sommer. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Lun 24 Jan 2011, 22:14 Lun 24 Jan 2011, 22:14 | |
|
Dernière édition par M.Marjani le Mar 25 Jan 2011, 19:28, édité 1 fois | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Mar 25 Jan 2011, 12:49 Mar 25 Jan 2011, 12:49 | |
| Merci pour vos réponses.
Avez-vous une autre méthode pour le 2ème, une méthode qu'on peut utiliser aux l'olympiades?
Merci d'avance. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Mar 25 Jan 2011, 19:08 Mar 25 Jan 2011, 19:08 | |
| ًon a selon cs : 2(a^2/(b+c) +b^2/(a+c) +c^2/(a+b))(a+b+c)>=(a+b+c)^2 Avec a+b+c=1. Ce qui donne cqfd.
| |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Mar 25 Jan 2011, 19:09 Mar 25 Jan 2011, 19:09 | |
| ًon a selon cs : 2(a^2/(b+c) +b^2/(a+c) +c^2/(a+b))(a+b+c)>=(a+b+c)^2 Avec a+b+c=1. Ce qui donne cqfd.
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Mer 26 Jan 2011, 22:17 Mer 26 Jan 2011, 22:17 | |
| Salut
On a le droit d'utiliser Caushy Schwarz aux Olympiades de TC ?? | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Mer 26 Jan 2011, 23:15 Mer 26 Jan 2011, 23:15 | |
| - Azerty1995 a écrit:
- Salut
On a le droit d'utiliser Caushy Schwarz aux Olympiades de TC ?? Je crois que OUI. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Jeu 27 Jan 2011, 00:00 Jeu 27 Jan 2011, 00:00 | |
| Pour la deuxième inégalité : D'après Caushy Shwartz : Posons S=(a+b)²/(c+1)+(b+c)²/(a+1)+(a+c)²/(b+1)) donc ((a+1)+(c+1)+(b+1))S=4S>=((a+b)+(a+c)+(b+c))=2²=4 Il s'ensuit que S>=1 CQFD  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  Jeu 27 Jan 2011, 14:00 Jeu 27 Jan 2011, 14:00 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Inégalités Sujet: Re: Inégalités  | |
| |
|
  | |
| | Inégalités |  |
|
