2 EXOS

Problème 1:
Trouver les nombres a, b et c tel que: |ax²+bx+c| 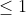( 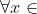[-1,1])
et la valeur de 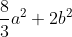soit maximale.



Problème 2:
Soit f(x) un fonction qui satisfait les deux conditions suivantes:
1)- .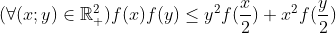
2)-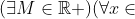[0;1])

Montrer que: .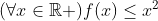

P.S: les solutions données doivent être détaillées.
Et pour la source de ces deux exos: C'est l'ancien programme de 1ere.

A VOS STYLOS.

Quelque soit M de R+ ?
Alors en prenant la limite, on a pour tout point x intérieur à [0,1], f(x)=0.
C'est bien ça ?

Une faute de frappe.
C'est plutôt Il existe
C édité.

Peut-il clarifier que veut dire elle sera maximale ?
Si c'est de l'ancien programme de 1ere, saches que la leçon majorant et minorant a été supprimé, donc on a pas les outils nécessaires de résoudre ce problème

ali-mes a écrit:

Problème 1:
Trouver les nombres a, b et c tel que: |ax²+bx+c| ( [1,1])
et la valeur de soit maximale.

C'est plutôt [-1;1]

Solution au problème 1 :

J'en suis pas sûr, j'espère qu'elle est juste :
* En prenant respectivement x=0, x=1, x=-1 nous obtenons |a+c|<=1 et |c|<=1 et |b|<=1
Donc 8/3a²<=8/3 ainsi que 2b²<=2.
De ce fait le maximum est atteint lorsque 8/3a²+2b²=14/3 Soit 8/3(a²-1)+2(b²-1)=0 puisque a²-1<=0 et b²-1<=0 donc a²=1 et b²=1

Il s'ensuit qu'il existe quatre cas : (1;1);(1-1);(-1;1);(-1;-1) et c € [-1;1].

t'as raison.
Je dois vérifier mes lunettes

C ÉDITÉ maintenant.

Ma réponse est juste ?
Je voudrais une confirmation s'il vous plaît

J'ai lu les grandes lignes, ça me parait juste.