Inégalité:

Voici l'énoncé:
Soit a et b deux rééls quelquonques.
Démontrez que .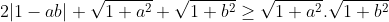
J'espère que l'inégalité est à la hauteur.
Bonne chance.

Après avoir utilisé la substitution trigonométrique a=tan(x) et b=tan(y) où x et y appartiennent à ]-pi/2, pi/2[, l'inégalité devient équivalente à 2|cos(x+y)|+|cos(x)|+|cos(y)|>=1, qui est vraie

Dijkschneier a écrit:

Après avoir utilisé la substitution trigonométrique a=tan(x) et b=tan(y) où x et y appartiennent à ]-pi/2, pi/2[, l'inégalité devient équivalente à 2|cos(a+b)|+|cos(a)|+|cos(b)|>=1, qui est vraie

Pourquoi? je ne vois pas que c'est trivial.

Il suffit donc de prouver que : 2|cos(x+y)|+|cos(x)|+|cos(y)|-1 >= 0, ce qui est vrai.
PS : la dernière inégalité peut-être prouvée en fixant y et en dérivant par rapport à x, après avoir ôté la valeur absolue en étudiant les cas où le cosinus est positif et les cas où il est négatif.