| | Bloqué sur un exo |  |
|
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Bloqué sur un exo Sujet: Bloqué sur un exo  Mer 30 Mar 2011, 12:36 Mer 30 Mar 2011, 12:36 | |
| Le plan est muni d'un repère orthonormé . Soit (H) une hyperbole dont l'équation est 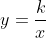 et 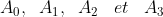 sont des points de (H). On dessine 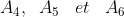 sur (H) tel que //\left%20(%20A_{0}A_{1}%20\right%20)) et //\left%20(%20A_{1}A_{2}%20\right%20)) et //\left%20(%20A_{2}A_{3}%20\right%20)) . Montrer que le trajet 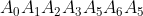 est fermé ( ou 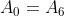 ). | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Mar 05 Avr 2011, 15:47 Mar 05 Avr 2011, 15:47 | |
| J'attends impatiemment vos réponses !!  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Mar 05 Avr 2011, 15:49 Mar 05 Avr 2011, 15:49 | |
| P.S: J'ai trouvé cet exo dans un olympiade de 1ere et dans un old-bouquain de 1ere ........ | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Ven 08 Avr 2011, 23:34 Ven 08 Avr 2011, 23:34 | |
| Finalement j'ai résolu cet exo.
Pour ceux qui sont intéressés par la solution, je vais la poster plus tard.
Dernière édition par ali-mes le Ven 08 Avr 2011, 23:52, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Ven 08 Avr 2011, 23:49 Ven 08 Avr 2011, 23:49 | |
| | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Sam 09 Avr 2011, 00:52 Sam 09 Avr 2011, 00:52 | |
| hh T'as pas constate que tu parles tout seul , hh ! just kidding  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Dim 10 Avr 2011, 02:34 Dim 10 Avr 2011, 02:34 | |
| Je sais !!! le merde c k personne ne participe dans cette rubrique c vraiment not-motivant !!! | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Jeu 14 Avr 2011, 20:22 Jeu 14 Avr 2011, 20:22 | |
| xDDD!! Parler tout seul! Meilleur chose!! Alors la solution? | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Jeu 14 Avr 2011, 23:03 Jeu 14 Avr 2011, 23:03 | |
| men ba3d o n werihalek fel 9issem mad5afxi a konika !!!  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Ven 15 Avr 2011, 07:33 Ven 15 Avr 2011, 07:33 | |
| Hello !!! Je viens de résoudre cet exo ! En fait il n’est pas difficile, il faut un peu de méthode et de l’organisation !! Soit x_n l’abscisse de A_n. Montrer que A_0=A_6 revient à dire que x_0=x_6 (puisque les deux points appartiennent à la courbe représentative d’une fonction injective) Il faut d’abord préciser que deux droites sont paralleles si et seulement si les deux coefficients directeurs sont égaux !!!!. %20\%20(A_{0}A_{1})%20\%20//%20\%20(A_{3}A_{4})\\%20Soit%20\%20a%20\%20le%20\%20coefficient%20\%20directeur%20\%20de%20\%20A_{0}A_{1}%20\%20et%20\%20A_{3}A_{4}%20\\%20\\%20ax_{0}+b=y_{0}=%20\frac{k}{x_{0}%20}%20\\%20ax_{1}+b=y_{1}=%20\frac{k}{x_{1}%20}%20\\%20Donc%20\%20\%20\%20a(x_{1}-x_{0})=%20k(%20\frac{1}{x_{1}}%20-\frac{1}{x_{0}})=%20-k(%20\frac{x_{1}-x_{0}}{x_{0}x_{1}})%20\\\%20Soit%20\%20a=\frac{-k}{x_{0}x_{1}}%20\\%20\\%20ax_{3}+b'=y_{3}=%20\frac{k}{x_{3}%20}%20\\%20ax_{4}+b'=y_{4}=%20\frac{k}{x_{4}%20}%20\\%20Donc%20\%20\%20\%20a(x_{4}-x_{3})=%20k(%20\frac{1}{x_{4}}%20-\frac{1}{x_{3}})=%20-k(%20\frac{x_{4}-x_{3}}{x_{4}x_{3}})%20\\%20Soit%20\%20a=\frac{-k}{x_{3}x_{4}}%20\\%20\\%20Donc%20\%20\%20\%20\frac{-k}{x_{3}x_{4}}%20=%20\frac{-k}{x_{0}x_{1}}%20\\%20Soit%20\%20\%20\%20\%20x_{3}x_{4}=x_{0}x_{1}%20\\%20\\%20Ainsi%20\%20\%20\%20\%20x_{4}=\frac{x_{0}x_{1}}{x_{3}}) \%20(A_{0}A_{1})%20\%20//%20\%20(A_{3}A_{4})\\%20De%20\%20la%20\%20m%C3%AAme%20\%20mani%C3%A8re%20\%20on%20\%20obtient%20\%20:%20\\%20x_{5}=\frac{x_{2}x_{1}}{x_{4}}%20\\%20En%20\%20rempla%C3%A7ant%20\%20x_{4}%20\%20par%20\%20sa%20\%20valeur%20\%20on%20\%20obtient%20\%20:%20\\%20\\%20x_{5}=\frac{x_{2}x_{3}}{x_{0}}%20\\%20\\%203)%20\%20(A_{5}A_{6})%20\%20//%20\%20(A_{2}A_{3})\\%20De%20\%20la%20\%20m%C3%AAme%20\%20mani%C3%A8re%20\%20on%20\%20obtient%20\%20:%20\\%20x_{6}=\frac{x_{3}x_{2}}{x_{5}}%20\\%20En%20\%20rempla%C3%A7ant%20\%20x_{5}%20\%20par%20\%20sa%20\%20valeur%20\%20on%20\%20obtient%20\%20:%20\\%20\\%20x_{6}=x_{0}%20\\) Voila, J’attends vos remarques !!
Dernière édition par Nayssi le Ven 15 Avr 2011, 12:28, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Ven 15 Avr 2011, 12:16 Ven 15 Avr 2011, 12:16 | |
| Parfait ....  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 | |
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Ven 15 Avr 2011, 12:28 Ven 15 Avr 2011, 12:28 | |
| Oui exactement!!!!
Je corrige! | |
|
  | |
Loliiiita
Habitué
 Nombre de messages : 18 Nombre de messages : 18
Age : 28
Date d'inscription : 23/04/2011
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  Dim 24 Avr 2011, 22:52 Dim 24 Avr 2011, 22:52 | |
| c un exo de tronc commun sa ? ^^" | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Bloqué sur un exo Sujet: Re: Bloqué sur un exo  | |
| |
|
  | |
| | Bloqué sur un exo |  |
|
