|
| | Problème |  |
| | | Auteur | Message |
|---|
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Problème Sujet: Problème  Sam 09 Avr 2011, 15:17 Sam 09 Avr 2011, 15:17 | |
| Yo.
Voici un problème pensé par Just-Abdess et qui, je pense, vous intéressera :
Soit ABCD un quadrilatère cyclique. Les diagonales AC et BD se coupent en E. Soit E_B la projection de E sur BC. On note P, N et Q les milieux de AB, CD et BC respectivement. Prouver que P, N, Q et E_B sont cocycliques. | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Problème Sujet: Re: Problème  Sam 09 Avr 2011, 17:33 Sam 09 Avr 2011, 17:33 | |
| Très Joli Problème. En lisant l'énnoncé pour la première fois, on dirait qu'il ne s'agit que d'un simple chasse d'angle, mais tous ceux qui ont essayé ce problème ont surement remarqué qu'il est loin d'être facile. Solution:Soit F le point d'intersection AD et BC, G celui de AB et DC. On note A_1, E_A, E_B et B_1 les points d'intersections du cercle de diamètre FE avec CA, FA, FB et DB respectivement. Soit M le mileu du segement FE et O le centre du cercle circonscrit au quadrilatère ABCD. Soit X le point d'intersection de OG et FE. 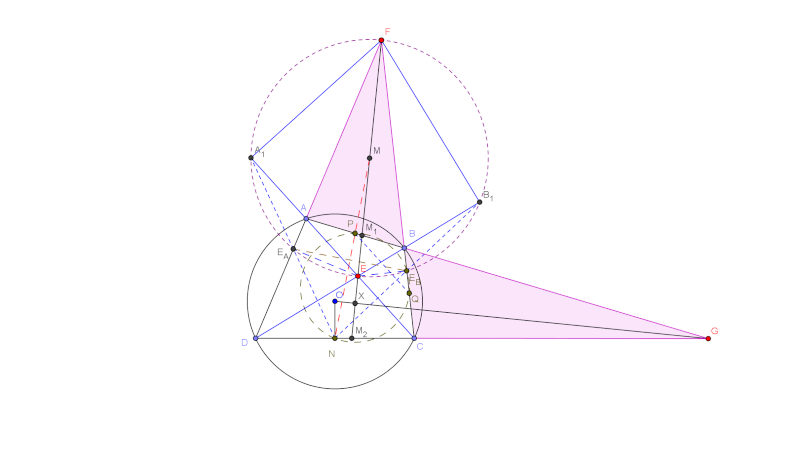 D'après le lemme que j'ai prouvé ici, le quadrilatère XONM_2 est cyclique, les quadrilatères FE_AEE_B et OPGN sont aussi cycliques, ainsi, on retrouve que: angle{NPB}+angle{BE_BE_A}=angle{GON}+angle{E_AEF}=angle{DFM_2}+angle{ADC}+angle{E_AEF}=270-angle{PBE_B}. D'où NP est perpendiculaire à E_AE_B. D'après Newton-Gauss, les points N, P et M sont collinéaires. Ainsi MN est la médiatrice de E_AE_B. (+) Soit N_1 le point d'intersection de A_1E_A et B_1E_B. En appliquant le theorème de Pascal sur l'hexagone A_1E_AFE_BB_1E, les points N_1, D et C sont collinéaires. Il est claire que angle{E_BEB}=angle{E_AEA}, donc angle{B_1FE_B}=angle{A_1FE_A} ainsi angle{B_1FE_A}=angle{A_1FE_B}, on en déduit que: angle{N_1E_BE_A}=angle{N_1E_AE_B} et par conséquent, le point N_1 appartient à la médiatrice de E_AE_B, et puisque M l'est aussi, on arrive à ce que MN_1 est la médiatrice de E_AE_B. (++) De (+) et (++) on déduit que N_1=N. De ceci, on a: angle{PNE_B}= 90-angle{E_AE_BN}=90-angle{DFB_1}=angle{ADB}=angle{PQB}. D'où on déduit finalement que P, N, Q et E_B sont cocycliques. P.S: Si il y a des erreurs dans cette solution, veuillez me les signaler pour que je puisse les corriger. | |
|   | | mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Problème Sujet: Re: Problème  Sam 09 Avr 2011, 17:50 Sam 09 Avr 2011, 17:50 | |
| - MohE a écrit:
- Très Joli Problème.
En lisant l'énnoncé pour la première fois, on dirait qu'il ne s'agit que d'un simple chasse d'angle, mais tous ceux qui ont essayé ce problème ont surement remarqué qu'il est loin d'être facile.
Solution:
Soit F le point d'intersection AD et BC, G celui de AB et DC. On note A_1, E_A, E_B et B_1 les points d'intersections du cercle de diamètre FE avec CA, FA, FB et DB respectivement. Soit M le mileu du segement FE et O le centre du cercle circonscrit au quadrilatère ABCD. Soit X le point d'intersection de OG et FE.

D'après le lemme que j'ai prouvé ici, le quadrilatère XONM_2 est cyclique, les quadrilatères FE_AEE_B et OPGN sont aussi cycliques, ainsi, on retrouve que:
angle{NPB}+angle{BE_BE_A}=angle{GON}+angle{E_AEF}=angle{DFM_2}+angle{ADC}+angle{E_AEF}=270-angle{PBE_B}. D'où NP est perpendiculaire à E_AE_B. D'après Newton-Gauss, les points N, P et M sont collinéaires. Ainsi MN est la médiatrice de E_AE_B. (+)
Soit N_1 le point d'intersection de A_1E_A et B_1E_B. En appliquant le theorème de Pascal sur l'hexagone A_1E_AFE_BB_1E, les points N_1, D et C sont collinéaires. Il est claire que angle{E_BEB}=angle{E_AEA}, donc angle{B_1FE_B}=angle{A_1FE_A} ainsi angle{B_1FE_A}=angle{A_1FE_B}, on en déduit que: angle{N_1E_BE_A}=angle{N_1E_AE_B} et par conséquent, le point N_1 appartient à la médiatrice de E_AE_B, et puisque M l'est aussi, on arrive à ce que MN_1 est la médiatrice de E_AE_B. (++)
De (+) et (++) on déduit que N_1=N.
De ceci, on a: angle{PNE_B}= 90-angle{E_AE_BN}=90-angle{DFB_1}=angle{ADB}=angle{PQB}. D'où on déduit finalement que P, N, Q et E_B sont cocycliques.
P.S: Si il y a des erreurs dans cette solution, veuillez me les signaler pour que je puisse les corriger. Super ! Bravo ! | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Problème Sujet: Re: Problème  Dim 10 Avr 2011, 15:36 Dim 10 Avr 2011, 15:36 | |
| Impressionnant.
On peut aussi imaginer une solution qui utilise les nombres complexes, puisque la configuration du problème offre un cadre idéal pour l'utilisation des complexes. | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Problème Sujet: Re: Problème  Dim 10 Avr 2011, 16:41 Dim 10 Avr 2011, 16:41 | |
| - Dijkschneier a écrit:
- Impressionnant.
On peut aussi imaginer une solution qui utilise les nombres complexes, puisque la configuration du problème offre un cadre idéal pour l'utilisation des complexes. Oui, Nos amis l'ont tous prouvé en utilisant les nombres complexes, c'est en effet la solution la plus facile à trouver pour ce problème, c'est aussi la deuxième méthode qu'on essaie lorsque le chasse angle n'abouti à aucun résultat. Mais il faut toujours chercher la beauté. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Problème Sujet: Re: Problème  | |
| |
|   | | | | Problème |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
