| | Marathon De Géométrie |  |
|
+22Oty SM.OMAR yasserito az360 boubou math momo1729 maths_lady diablo902 ali-mes SarakZit.A King Dijkschneier Bensouda majdouline Mehdi.O darkpseudo Sylphaen Sporovitch MohE nmo extrajijo Mr.Wajih 26 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 17 Mar 2011, 20:10 Jeu 17 Mar 2011, 20:10 | |
| - Sylphaen a écrit:
Problème 20 :
ABC un triangle dont les angles sont aiguës . M le milieu de [BC] . P la projection orthogonal de l'orthocentre H sur AM.
MQ : AM.PM=BM² - Spoiler:
 Soient %20\cap%20(BC)) et %20\cap%20(AB)) Soit (C) le cercle passant par A, B et P. On se propose de montrer que (MB) est tangente au cercle, ce qui permettrait de conclure en considérant la puissance de M par rapport à (C). Puisque AHP et AA'M sont semblables, il vient PMB = AHP Puisque APHC' est inscriptible, il vient AHP = AC'P = 180 - BC'P Par suite, PMB = 180 - BC'P, et C'PMB est semblable. Maintenant, MBP = MC'P = MC'C + CC'P. Or MC'C = MCC', car MCC' est isocèle, car M est le centre du triangle CBC'. On a alors : MC'C = MCC' = 90 - B = BAA'. Et : CC'P = HC'P = HAP. Par suite : MBP = BAA' + HAP = BAM, et par suite (BM) est tangente à (C).
Et je n'ai pas de problème à proposer pour le moment. | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 09:52 Ven 18 Mar 2011, 09:52 | |
| - Sylphaen a écrit:
Problème 20 :
ABC un triangle dont les angles sont aiguës . M le milieu de [BC] . P la projection orthogonal de l'orthocentre H sur AM.
MQ : AM.PM=BM² - Spoiler:
SOit A' le projeté hortogonal de A sur BC et C' le projeté horthogonal de C sur [AB]; APHC' est inscriptible et A'AB=MCC'=MC'C (car les 2 triangles AA'B et CC'A sont semblables ) ==> (MC') est tangeant au cercle (APHC') donc AP.AM=MC'²=MB² .
- Dijkschneier a écrit:
- et je n'ai pas de problème à proposer pour le moment
Probleme 21SOient A,B,C,D 4 points d'un cercle tels que (AC) et (BD) se coupent en E , (AD) et (BC) se coupent en F tel que (AB) et CD) ne sont pas parallèles. Montrer que C,D,E,F sont cocycliques si et seulement si (EF) est perpendiculaire avec (AB) | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 13:31 Ven 18 Mar 2011, 13:31 | |
| Solution : - Spoiler:
 On a C,D,E,F cocyclique <==> <ECF=<FDE = pi/2 ( car <ACB+<ADB=pi ) <==> A et l'horthocentre du triangle BEF ==> (BA) et (EF) perpendiculaire. Si (EF)et(AB) perpendiculaire , on a : <ACD=<ABD ( cocycliques ) de plus les triangles ACD et AEF sont semblables donc <ACD = <AFE on en conclu que les triangles ABD et AFT sont semblables ( T le point d'intersection ) et donc <ADB = <ATF = pi/2 vu que< ADB+<ACB=pi on a <ADB=<ACB=pi/2 et donc <ADE =<ACF=pi/2 CQFD .
Je n'ai pas de problème à proposé pour l'instant | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 15:15 Ven 18 Mar 2011, 15:15 | |
| - darkpseudo a écrit:
- Solution :
On a
C,D,E,F cocyclique <==> <ECF=<FDE = pi/2 ( car <ACB+<ADB=pi )
<==> A et l'horthocentre du triangle BEF ==> (BA) et (EF) perpendiculaire.
Si (EF)et(AB) perpendiculaire , on a :
<ACD=<ABD ( cocycliques ) de plus les triangles ACD et AEF sont semblables donc
<ACD = <AFE on en conclu que les triangles ABD et AFT sont semblables ( T le point d'intersection ) et donc <ADB = <ATF = pi/2
vu que< ADB+<ACB=pi on a <ADB=<ACB=pi/2 et donc <ADE =<ACF=pi/2 CQFD .
Je n'ai pas de problème à proposé pour l'instant Merci de bien expliquer la partie en gras -C'est quoi le point T ? -quel es l'ordre des point (A,B,C,D) que t'as choisi car cela n'est pas clair dans la figure ? -Pourquoi ACD et AEF sont semblables ? | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 17:51 Ven 18 Mar 2011, 17:51 | |
| Le point T est le point d'intersection de (AB) et (EF) .
L'ordre pris est A==>C==>B==>D .
Les deux triangles sont semblables car il y a une similitude de centre A et qui renvoi un triangle vers l'autre , cette similitude existe car l'angle <ETA est droit , maintenant quand j'ai relu la preuve je me rend compte que j'aurai juste pour m'arrêter aux deux triangles semblable vu que c'est suffisant pour dire que les points sont cocycliques .
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 18:49 Ven 18 Mar 2011, 18:49 | |
| Je n'ai pas très bien compris l'argument de darkpseudo pour la partie (<=) et en particulier l'existence de la similitude, mais je voudrais noter que cette partie peut se faire plus simplement en considérons E' = (BC) Inter (C') où (C') est le cercle passant par D,C et F et en utilisant (=>). | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 19:42 Ven 18 Mar 2011, 19:42 | |
| Tu voulais dire E'=(BD) inter (C') je présume ? Oui effectivement dans ce cas on montrerais que E'=E .
Problème 22 :
Soit CO_1 et CO_2 deux cercles de même rayon se coupant en A et B . Soit O LE Milieu de AB.
CD une corde de CO_1 qui passe par O [CD] coupe CO_2 en P ( la première intersection ) de même [EF] une corde de CO_2 qui passe par O et qui coupe CO_1 en Q ( la première intersection ) . Prouvez que AB; CQ et EP sont concourantes .
Dernière édition par darkpseudo le Dim 20 Mar 2011, 17:33, édité 1 fois | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 20:04 Ven 18 Mar 2011, 20:04 | |
| - Dijkschneier a écrit:
- Je n'ai pas très bien compris l'argument de darkpseudo pour la partie (<=) et en particulier l'existence de la similitude, mais je voudrais noter que cette partie peut se faire plus simplement en considérons E' = (BC) Inter (C') où (C') est le cercle passant par D,C et F et en utilisant (=>).
Bonsoir Dijkschneir! J'arrive toujours pas à trouver une solution simple suivant ce que tu as donné comme indices. Si tu n'y trouve aucun problème et que tu es sur de ne pas avoir commis une erreure, explique moi comment procéder si'il te plait, j'en serais très reconnaisant. Bonsoir Darkpseudo! J'arrive pas à comprendre pourquoi <ETA= 90 implique l'existence d'une similitude qui renvoie le triangle ACD au triangle AEF. Explique moi s'il te plait. Si aucune explication claire n'est proposée, le problème de Sporovitch serai toujours celui à résoudre en premier dans le jeu. En effet, une solution existe mais elle est plus compliquée que les deux tentatives déjà proposées. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 20:39 Ven 18 Mar 2011, 20:39 | |
|
Dernière édition par Dijkschneier le Mar 05 Fév 2013, 04:33, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 18 Mar 2011, 21:18 Ven 18 Mar 2011, 21:18 | |
| - darkpseudo a écrit:
- Solution :
- Spoiler:
 On a C,D,E,F cocyclique <==> <ECF=<FDE = pi/2 ( car <ACB+<ADB=pi ) <==> A et l'horthocentre du triangle BEF ==> (BA) et (EF) perpendiculaire. Si (EF)et(AB) perpendiculaire , on a : <ACD=<ABD ( cocycliques ) de plus les triangles ACD et AEF sont semblables donc <ACD = <AFE on en conclu que les triangles ABD et AFT sont semblables ( T le point d'intersection ) et donc <ADB = <ATF = pi/2 vu que< ADB+<ACB=pi on a <ADB=<ACB=pi/2 et donc <ADE =<ACF=pi/2 CQFD .
Je n'ai pas de problème à proposé pour l'instant Voilà pour donné une preuve clair : - Spoiler:
Pour la seconde partie de la démo je propose une autre approche (directement prise de celle de Dijck s'il le permet bien sûr ) ; On pose E' le point d'intersection de (BD) avec le cercle circonscrit à DCF En supposant que <ATF = pi/2 et on se propose de montrer que E'=E auquel-cas on aurait prouvé que les points sont cocycliques : On a (DF) et (BT) ce coupent en A de plus on a <E'CF=<FDE donc <ACB=<ADB=pi/2 et donc <E'CF=<FDE=pi/2 ==> (AB) (DF) et (CE') sont concourantes en l'orthocentre du triangle or (DF) et (AB) ce coupe déjà en A et donc (CE') passe par A mais on a déjà E l'intersection de (AC) et (BD) donc E=E' CQFD . 
| |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 20 Mar 2011, 12:53 Dim 20 Mar 2011, 12:53 | |
| Bonjour Darkpseudo! Un problème figure dans ta dernière solution : C'est l'ordre des points, tu ne l'as pas respecté. En tout cas voiçi une solution pour avancer le jeu. Solution 21:Lemme. Soit ABCD un quadrilatère cyclique dont les diagonals se coupent en G. Supposons que AD coupe BC en E, et que AB coupe DC en F. Alors (FG) est perpendiculaire à (EO), où O est le centre du cercle circonscrit au quadrilatère ABCD.Preuve. Soit X le point d'intersection des cercles circonscrits aux triangles ABG et DCG. D'après le theorème des axes radicaux, les points X, G et F sont collinéaires. D'un autre coté, on a: angle{BXC}=2angle{BDC}=angle{BOC} d'où BXOC est cyclique. De même AXOD est cyclique, ainsi d'après le theorème des axes radicaux, on déduit que E, X et O sont collinéaires. Or, on a: angle{OXG}= angle{BDC}+angle{OBC}=90°. D'où (FG) et (EO) sont perpendiculaires. Ceci achève la preuve du lemme. Retour au problème.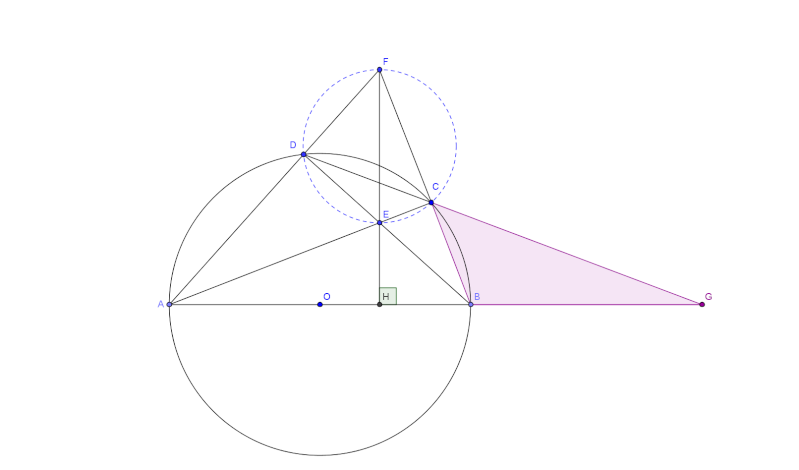 o. o. Si FDEC est cyclique: On vérifie directement que E est l'orthocentre de FAB et par conséquent (FE) est perpendiculaire à (AB). o. Si (FE) est perpendiculaire à (AB). Soit H le point d'intersection de (FE) et (AB), G celui de DC et AB ( Ce point existe d'après l'énnoncé), D'après le lemme démontré, (FE) est perpendiculaire à (OG), mais on à déjà (HG) qui est perpendiculaire à (FE), d' où O£(HG), ainsi AB est un diamètre du cercle (O), il s'ensuit que E est l'orthocentre de ABF, et par conséquent FDEC est cyclique. Le problème à résoudre maintenant est celui de Darkpseudo. @Darkpseudo. S'il te plait, relit le problème que tu as proposé. L'ordre des points n'y est pas précisé, par exemple la corde CD coupe CO_2 en deux points et on ne sait pas laquelle d'entre eux on doit choisir. Ce serait gentil de ta part si tu nous fais une figure. Merci! | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 20 Mar 2011, 17:46 Dim 20 Mar 2011, 17:46 | |
| - MohE a écrit:
- Bonjour Darkpseudo!
Un problème figure dans ta dernière solution : C'est l'ordre des points, tu ne l'as pas respecté. En tout cas voiçi une solution pour avancer le jeu.
Solution 21:
Lemme.
Soit ABCD un quadrilatère cyclique dont les diagonals se coupent en G. Supposons que AD coupe BC en E, et que AB coupe DC en F. Alors (FG) est perpendiculaire à (EO), où O est le centre du cercle circonscrit au quadrilatère ABCD.
Preuve.

Soit X le point d'intersection des cercles circonscrits aux triangles ABG et DCG.
D'après le theorème des axes radicaux, les points X, G et F sont collinéaires. D'un autre coté, on a:
angle{BXC}=2angle{BDC}=angle{BOC} d'où BXOC est cyclique.
De même AXOD est cyclique, ainsi d'après le theorème des axes radicaux, on déduit que E, X et O sont collinéaires. Or, on a: angle{OXG}= angle{BDC}+angle{OBC}=90°.
D'où (FG) et (EO) sont perpendiculaires. Ceci achève la preuve du lemme.
Retour au problème.

o. Si FDEC est cyclique:
On vérifie directement que E est l'orthocentre de FAB et par conséquent (FE) est perpendiculaire à (AB).
o. Si (FE) est perpendiculaire à (AB).
Soit H le point d'intersection de (FE) et (AB), G celui de DC et AB ( Ce point existe d'après l'énnoncé), D'après le lemme démontré, (FE) est perpendiculaire à (OG), mais on à déjà (HG) qui est perpendiculaire à (FE), d' où O£(HG), ainsi AB est un diamètre du cercle (O), il s'ensuit que E est l'orthocentre de ABF, et par conséquent FDEC est cyclique.
Le problème à résoudre maintenant est celui de Darkpseudo.
@Darkpseudo. S'il te plait, relit le problème que tu as proposé. L'ordre des points n'y est pas précisé, par exemple la corde CD coupe CO_2 en deux points et on ne sait pas laquelle d'entre eux on doit choisir. Ce serait gentil de ta part si tu nous fais une figure. Merci! Tout cela est parfait. Mais comment avez-vous eu l'idée de cette lemme, est-ce-que vous l'avez constaté directement du schéma, ou bien existe-elle déjà?  | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 20 Mar 2011, 18:39 Dim 20 Mar 2011, 18:39 | |
| L'idée d'un lemme en générale, ne vient pas par hasard, c'est souvent le résultat d'une suite de remarques et de déductions souvent jugés difficiles. Néanmoins, ce problème, étant facile, nous ramène directement à prouver ce lemme, c'est la premier chose dont on pense une fois qu'on considère le point G. De mon côté, je le connaisais déjà (très connu), mais ce que j'ai trouvé c'est la nouvelle preuve présenté ci-dessus. Pourquoi?
La première fois que j'avais affaire à ce lemme, je l'avais prouvé avec des relations métriques, la deuxième fois, j'avais pensé à une solution projective qui étais beaucoup plus simple, cette fois-ci j'ai pensé à une solution synthétique, qui est plus intelligente (le point X) et surtout beaucoup plus jolie. | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 24 Mar 2011, 19:23 Jeu 24 Mar 2011, 19:23 | |
| - Bensouda a écrit:
- SOIS a,b et c les longueurs d'un triangle et S sa surface MQ :
 Un classique : D'après la formule de Héron et l'inégalité :  on a :   Et c'est fini. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 24 Mar 2011, 20:36 Jeu 24 Mar 2011, 20:36 | |
| - darkpseudo a écrit:
Problème 22 :
Soit CO_1 et CO_2 deux cercles de même rayon se coupant en A et B . Soit O LE Milieu de AB.
CD une corde de CO_1 qui passe par O [CD] coupe CO_2 en P ( la première intersection ) de même [EF] une corde de CO_2 qui passe par O et qui coupe CO_1 en Q ( la première intersection ) . Prouvez que AB; CQ et EP sont concourantes . - Spoiler:
.  Solution : ( En effet ces droites peuvent être parallèles ... ) Il est clair que O est le milieu de [O 1O 2 ].. L'homothétie de centre O et de rapport -1 envoie (C,O 1) en (C,O 2 ) . Alors on a immédiatement OD=OP et OQ=OF . Considérons C' la seconde intersection de (OP) et (C,O 2) . On a OC=OC' et la puissance de O par rapport au cercle (C,O 2) = OE.OF=OP.OC'=OP.OC ce qui implique que : 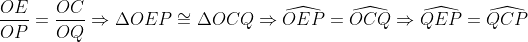 Donc les points E,C,P,Q sont cocyclique , Et d'après le théorème des axes radicaux on obtient immédiatement le résultat voulu ..
Problème 23 : Les diagonales AC et CE d'un hexagone régulier ABCDEF sont divisées respectivement par des points intérieur M et N t.q 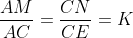 Déterminer la valuer de K pour que B,M et N soit alignés | |
|
  | |
Invité
Invité
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 27 Mar 2011, 18:24 Dim 27 Mar 2011, 18:24 | |
| voici ma solution pour ce joli p5 de 1982 : - Spoiler:
posons a=AB=BC=CD=DE=EF alors AC=CE=a*3^1/2 (al kachi dans BAC )
supposons B M N alignés
CBN est rectangle en C (ACN=60 et ACB=30) donc par pythagore BN=a*(1+3k^2)^0.5
sin MBC=sinNBC=k*3^0.5/(1+3k^2)^0.5 donc la loi des sinus dans MBC donne
MB=(a/2)*(1-k)*(1+3k^2)^0.5/k
donc MN=NB-BM=a*(1+3k^2)^0.5(1.5-0.5k)
d'autre part ,la loi des sinus dans MCN donne en tenant compte de sin MNC=a/BN
MN=1.5*(1+3k^2)^0.5*a*(1-k)
en égalisant les deux expressions obtenues de MN on trouve k=1/3^0.5
problème 24:(shortlist) soit ABC un triangle et (L) la droite passant par C et parallèle à (BA) la bisse. interne de A coupe (BC) en D et (L) en E " " "" " """"""""""de B """"""" (AC) en F et (L) en G prouver que si GF=ED alors CB =AC
Dernière édition par salimt le Mer 30 Mar 2011, 00:10, édité 1 fois |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 29 Mar 2011, 18:40 Mar 29 Mar 2011, 18:40 | |
| AC=BC, non ?  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 29 Mar 2011, 19:26 Mar 29 Mar 2011, 19:26 | |
| Si c'est en effet le cas, alors la loi des sinus kills it. | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 29 Mar 2011, 19:46 Mar 29 Mar 2011, 19:46 | |
| Apparement le problème doit être reformulé (si salim le permet bien-sûr): Problème 24:Soit ABC un triangle et (L) la droite passante par C et parallèle à AB. La bissectrice intérieures de <A coupe BC et (L) en D et E respectivement. De même, la bissectrice intérieure de <B coupe AC et (L) en F et G respectivement. Supposons que GF=DE, Prouver que CB=CA. @ salim: merci d'avoire participer dans ce jeu. - Dijkschneier a écrit:
- Si c'est en effet le cas, alors la loi des sinus kills it.
Je voudrais bien voir ta solution complète où la loi des sinus "kills it". De ma part, j'ai trouvé deux solutions, la première se base sur la loi des sinus et la trigonométrie; La deuxième est synthétique. Merci d'avance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 29 Mar 2011, 19:59 Mar 29 Mar 2011, 19:59 | |
| OK.  ACE et BCG sont isocèles. Dans DCE, la loi des sinus donne : ED = ab/(b+c) sin(B)/sin(A/2) (le théorème de la bissectrice a été utilisé) De même dans FCG : FG = ab/(a+c) sin(A)/sin(B/2) En mettant en équation, il vient (2p-a)sin(A)sin(A/2) = (2p-b)sin(B)sin(B/2), où p est le demi-périmètre, ce qui donne (2p-2Rsin(A))sin(A)sin(A/2) = (2p-2Rsin(B))sin(B)sin(B/2) Le problème est donc réduit à démontrer que la fonction f(x)=(constante-sin(x))sin(x)sin(x/2) est injective, ce qui peut se faire avec des factorisations trigonométriques. | |
|
  | |
Invité
Invité
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mer 30 Mar 2011, 00:15 Mer 30 Mar 2011, 00:15 | |
| oui c'est édité  pour la solution de Dijk. les factorisations trigonométriques c'est pas vraiment évident :à détailler ! |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mer 30 Mar 2011, 13:50 Mer 30 Mar 2011, 13:50 | |
| Je suis arrivé à factoriser f(A)-f(B) par sin(A/4-B/4) (sauf erreur) et j'ai cru par erreur que le reste était évident.
Mais non : il n'est pas facile de montrer que l'autre terme qui ressort de la factorisation ne s'annule pas (ce qui aurait pu impliquer que A=B). | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 01 Avr 2011, 16:05 Ven 01 Avr 2011, 16:05 | |
| Solution du problème 24 : Assumons que DE=FG et Montrons que ABC est isocèle en C. Tout d'abord remarquons que : 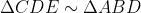 et 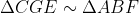 . Il s'ensuit que : \Rightarrow&space;\frac{sin(\angle&space;B)}{DE}=\frac{sin(\angle&space;\frac{A}{2})}{DC}\wedge&space;\frac{sin(\angle&space;A)}{FG}=\frac{sin(\angle&space;\frac{B}{2})}{CF}\Rightarrow&space;\frac{sin(\angle&space;A)}{sin(\angle&space;\frac{B}{2})}.CF=\frac{sin(\angle&space;B)}{sin(\angle&space;\frac{A}{2})}.DC) }{DC}=\frac{sin(\angle&space;C)}{AD}\wedge&space;\frac{sin(\angle&space;\frac{&space;B}{2})}{CF}=\frac{sin(\angle&space;C)}{BF}\Rightarrow&space;\frac{AD}{DC}.sin(\angle&space;\frac{A}{2})=\frac{BF}{CF}.sin(\angle&space;\frac{B}{2})\Rightarrow&space;\frac{sin(\angle&space;A)}{sin(\angle&space;B)}=\frac{BF}{AD}) Ainsi : 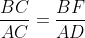 Nous savons que : ^{2})\wedge&space;AD^{2}=AB.AC(1-(\frac{BC}{AB+AC})^{2})) Maintenant pour simplifier posons 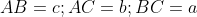 Ainsi l'équation devient : ^{2})}{bc(1-(\frac{a}{b+c})^{2})}\Leftrightarrow&space;(a+c)^{2}\frac{a}{b}=\frac{a+c-b}{b+c-a}.(b+c)^{2}\Leftrightarrow&space;a(a+c)².(b+c-a)=b(b+c)^{2}.(a+c-b)) Vu l'homogénité on peut supposer que a+b+c=1 Ainsi : ^{2}}{b(1-2b))}=\frac{(1-a)^{2}}{a(1-2a))}) Sachant que la fonction : =\frac{(1-x)^{2}}{x(1-2x)}) est injective , cela nous permet de conlure finalement que 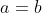 CQFD  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 01 Avr 2011, 16:17 Ven 01 Avr 2011, 16:17 | |
| xD, après 5 mintutes j'ai revu ma solution. En effet, à l'étape : 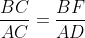 et les deux triangles BCF et ADC ont un angle commun C, et 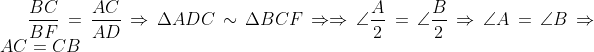 | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 02 Avr 2011, 13:26 Sam 02 Avr 2011, 13:26 | |
| Problème 25 :
Soit ABC est un triangle. Soit D un point de [AC] tel que BD=AB. Le cercle inscrit de ABC touche [AB] et [AC] en K et L respectivement. Soit J le centre du cercle inscrit de BDC.
Montrez que [KL] coupe [AJ] en son milieu.
Dernière édition par Mehdi.O le Mar 12 Avr 2011, 19:17, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  | |
| |
|
  | |
| | Marathon De Géométrie |  |
|
