| | MARATHON (un peu de géo) |  |
|
|
| Auteur | Message |
|---|
Ahmed Taha
Maître
 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: MARATHON (un peu de géo) Lun 17 Fév 2014, 22:32 | |
| salut a tous Je lance ce nouveau marathon pour bien se préparer aux olympiades de cette année (incha allah) les règles ils ont claire comme toujours : 1- chaque problème posté devrai avoir un numéro.
2- Les Solutions devrai être en spoiler .
3-Celui qui a trouvé la réponse, il doit poster un autre problème. Mais si la solution n'est pas trouvée pendant 3 jours, celui qui a posté le problème doit poster une réponse.
4- Veiller à ne pas répéter les problèmes .
5- Si quelqu'un arrive à trouver une solution sans avoir un nouveau exercice qu'il indique pour que quelqu'un d'autre le fait .
6- Expliciter les notations utilisées , si nécessaire .
7- Ne pas poster des solutions incomplètes et par conséquent , ne pas attendre de confirmation pour proposer un nouveau problème .
8- De préférence les énoncés et les solutions devraient être rédigé en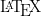 
Bon , commençons par ce problème : Problème 1 :On considère un trapèze ABCD tel que AB // CD, AB = 84 Et CD = 25. On suppose qu’il existe un cercle inscrit dans ce trapèze. Quel est le périmètre de ce trapèze. | |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: MARATHON (un peu de géo) Lun 17 Fév 2014, 23:18 | |
| Sol 1:- Spoiler:
Soit S la surface de ABCD, il est facile de prouver que S=pr/2 avec p le perimetre de ABCD, et r le rayon du cercle inscrit.
Or on sait également que S=(AB+CD).h/2 avec h=2r
=> p=2(AB+CD)= 218
RQ : il est possible de finir le probleme directement avec l'implication connue:
Un quadrilatère ABCD est circonscriptible <=> AB+CD=BC+AD
| |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| |
| | |
L-W-P
Maître
Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
| | Sujet: Re: MARATHON (un peu de géo) Mar 18 Fév 2014, 12:34 | |
| - solution 2:
solution exercice 2:
(a)
AM(vecteur)=AN(vecteur) ----> (AN)//(ME) (1)
BEC rectangle en E et N le milieu de l'hypoténuse [BC] alors NE=NC ----> NE=AM (2)
de (1) et (2) on aura que ANEM est un trapèze isocèle.
(b)
on a S(ANEM)=S(ABN)+S(AEN) (on a ABN et MDN des triangles isométriques)
alors S(ANEM)=1/2(S(ABN)+S(MDC))+S(AEN)
on a S(MEC)+S(AME)=((BE/2)*AM)/2+((BE/2)*EC)=S(AEN)
alors S(ANEM)=1/2(S(ABN)+S(MDC))+1/2(S(AEN)+S(AEN))
ce qui donne que
S(ANEM)= 1/2 S(ABCD)
Dernière édition par L-W-P le Mar 18 Fév 2014, 12:43, édité 1 fois | |
|
| | |
L-W-P
Maître
Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
| | Sujet: Re: MARATHON (un peu de géo) Mar 18 Fév 2014, 12:37 | |
| Jusqu'à maintenant j'ai pas d'exercice à poster, quelqu'un qu'il poste. | |
|
| | |
L-W-P
Maître
Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
| | Sujet: Re: MARATHON (un peu de géo) Mar 18 Fév 2014, 13:02 | |
| Problème 3
Les diagonales d'un trapèze ABCD de bases [AB] et [CD] se coupent en P.
Monter que S(PAB)+S(PCD)> S(PBC)+S(PDA). | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| |
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: MARATHON (un peu de géo) Mar 18 Fév 2014, 17:35 | |
| Solution peu elegante :'( - Solution au problème 4:
On considère le repère (D;DC,DA) => D(0;0) et C(1;0) et A(1;0) et D(1;1) On prend E(a,1), on a dès lors les équations (DE): y=(1/a).x et (AC): y=-x+1 P=(DE) inter AC => P( a/(1+a) ; 1/(1+a) ) Vu que (PF) est perpendiculaire à (ED) , on peut deduire que: (PF ): y=-ax+[(1+a²)/(1+a)] Et ensuuite on en deduit que F(1; (1-a)/(1+a) ) Mtn ayant les coordonnées des 3 points il est facile de verifier l'égalité donnée  Sauf erreur
| |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| |
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: MARATHON (un peu de géo) Jeu 20 Fév 2014, 17:41 | |
| - Indice :
vous pouvez considérer un point P de (CI) tel que PI=PB, Et montrer dès lors que ce point est bel et bien O ( en montrant que PI=PA), par chasse angles si vous voulez (Remarquez que APBC est inscriptible) .
| |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Jeu 20 Fév 2014, 18:31 | |
| Suite aux indices de legend-crush on peu en déduire que l'angle API = IPB (1), et du moment que I est dans (CI) et (CI) est la bissectrice de ABC donc (IP) bissectrice de AIB ce qui veut dire que l'angle AIP=PIB (2), (1) et (2) ==> les triangles API et PIB sont semblables et on a AP=PI donc AP =BP d’où le résultat | |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Jeu 20 Fév 2014, 19:17 | |
| Si vous confirmez ma solution, je poste un nouveau problème... | |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: MARATHON (un peu de géo) Jeu 20 Fév 2014, 21:44 | |
| - DAMP a écrit:
- Si vous confirmez ma solution, je poste un nouveau problème...
Desolé, je ne peux me concentrer complètement avec votre solution car je dois reviser pour des exam de demain, Mais ça parait correct à vue d'ensemble, et vous pouvez proposer un nouveau problème | |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Jeu 20 Fév 2014, 22:13 | |
| Soit ABC un triangle, les bissectrices des angles A, B et C coupe une deuxième fois le cercle circonscrit de ABC dans P,Q et R, respectivement. Montrez que AB+BC+AC<AP+BQ+AC | |
|
| | |
Lonely.Guy
Débutant
Nombre de messages : 8
Age : 27
Date d'inscription : 13/02/2014
| | Sujet: Re: MARATHON (un peu de géo) Ven 21 Fév 2014, 11:37 | |
| - DAMP a écrit:
- Soit ABC un triangle, les bissectrices des angles A, B et C coupe une deuxième fois le cercle circonscrit de ABC dans P,Q et R, respectivement. Montrez que AB+BC+AC<AP+BQ+AC
tu veux dire RC à la place de AC au 2éme sens n'est pas ! | |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Dim 23 Fév 2014, 22:19 | |
| Oui c'est ça pardon ! Devrai-je posté la solution ? | |
|
| | |
elmrini
Maître
 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
| | Sujet: Re: MARATHON (un peu de géo) Mer 26 Fév 2014, 13:28 | |
|
Dernière édition par elmrini le Mer 26 Fév 2014, 15:22, édité 1 fois | |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Mer 26 Fév 2014, 15:02 | |
| Euh le cercle circonscrit est le cercle autour du triangle (cercle passant par tous les sommets du triangle) ... (P,R,Q sont hors du triangle) | |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Mer 26 Fév 2014, 15:06 | |
| Bon, faire avancer les choses: voila quelques indices: - Spoiler:
Loie des sinus... Chasse d'angles... petit manipulation des formules trigonométriques
 | |
|
| | |
elmrini
Maître
Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
| | Sujet: Re: MARATHON (un peu de géo) Mer 26 Fév 2014, 15:24 | |
| - DAMP a écrit:
- Bon, faire avancer les choses: voila quelques indices:
- Spoiler:
Loie des sinus... Chasse d'angles... petit manipulation des formules trigonométriques
inattention dsl | |
|
| | |
elmrini
Maître
Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
| | Sujet: Re: MARATHON (un peu de géo) Mer 26 Fév 2014, 15:50 | |
| donc sa sera très facile. | |
|
| | |
DAMP
Féru
Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
| | Sujet: Re: MARATHON (un peu de géo) Mer 26 Fév 2014, 22:20 | |
| Bon voila la réponse pour faire avancer le marathon: Loi des sinus: 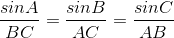 Par une chasse d'angles on montre que: 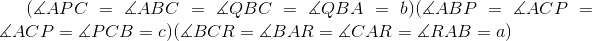 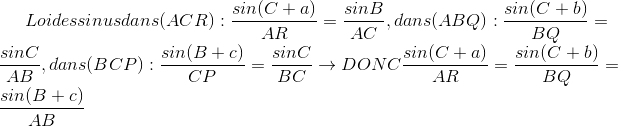 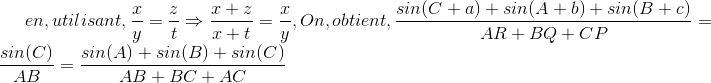  Enfin: AB+BC+AC<AR+BQ+RC Si quelqu’un a un exo qu'il le poste  | |
|
| | |
elmrini
Maître
Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
| | Sujet: Re: MARATHON (un peu de géo) Jeu 27 Fév 2014, 21:58 | |
| Problème 6 :
Soit ABC un triangle à angles aigus. Les pieds des hauteurs issues des sommets A,B et C sont respectivement D,E et F.
Montrer que DE+EF < BC, et déterminer les triangles pour lesquels l’égalité est réalisée. | |
|
| | |
elmrini
Maître
Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
| |
| | |
elmrini
Maître
Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
| | Sujet: Re: MARATHON (un peu de géo) Lun 03 Mar 2014, 15:39 | |
| voici un autre
Problème 7 :
Soit ABC un triangle est un point D a l’intérieur de celui-ci tel que : <DAC=<DCA=30 et <DBA=60 . soit E le milieu de [BC] . F un point de AC tel que : AF=2FC . Prouver que (DE) et (EF) sont perpendiculaire . | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: MARATHON (un peu de géo) | |
| |
|
| | |
| | MARATHON (un peu de géo) | |
|
