| | Marathon |  |
|
+12galillee56 younesmath2012 Humber Oty somat BTBICL aymas amigo-6 Top-Math alidos boubou math Yassirkirua 16 participants |
|
| Auteur | Message |
|---|
Yassirkirua
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 27
Date d'inscription : 03/02/2013
 |  Sujet: Marathon Sujet: Marathon  Sam 15 Juin 2013, 15:04 Sam 15 Juin 2013, 15:04 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 15 Juin 2013, 15:35 Sam 15 Juin 2013, 15:35 | |
| Solution exo 1 : - SOL:
Pour m=0 , on obtient : =f(f(n))+f(f(0))) , on pose f(f(0))=a et on remplace , dans l’équation initial , on a donc : =f(m)+f(n)-2a) ou encore -2a=f(m)-2a+f(n)-2a) (pour tous m,n entiers naturels) , on pose : =f(m)-2a) ,l’équation précédente s’écrit : \in&space;IN):g(m+n)=g(m)+g(n)) qui n'est rien d'autre que l'équation de Caushy,on a donc =\alpha&space;n) avec alpha entier naturel , on remplaçant dans l’équation initial , on trouve que seulement la fonction nul et l’identité sont des solutions
| |
|
  | |
Yassirkirua
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 27
Date d'inscription : 03/02/2013
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 15 Juin 2013, 15:37 Sam 15 Juin 2013, 15:37 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 15 Juin 2013, 15:47 Sam 15 Juin 2013, 15:47 | |
| EXO 2 :
Dans le triangle ABC, la bissectrice de l'angle au sommet C intersecte le cercle circonscrit et la médiatrice des côtés BC et CA aux points R, P et Q, respectivement. Les milieux de
BC et CA sont S et T, respectivement. Démontrer que les triangles RQT et RPS ont la même aire. | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 15 Juin 2013, 17:46 Sam 15 Juin 2013, 17:46 | |
| Mr Boubou vérifie stp est ce que l'énoncé est juste  | |
|
  | |
Top-Math
Féru
 Nombre de messages : 59 Nombre de messages : 59
Age : 27
Date d'inscription : 11/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 15 Juin 2013, 18:32 Sam 15 Juin 2013, 18:32 | |
| Désolé, je n'ai pas le temps pour y penser complètement mais je vous propose de distinguer deux cas :
AC=BC
AC différent de BC.
Puisque dans le premier le résultat est trivial.
Goodbye. | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 | |
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 15:05 Dim 16 Juin 2013, 15:05 | |
| L'exo est resté sans solution pour longtemps, pour ne pas bloquer le marathon dés le debut , je poste ma solution en spoiler :   " /> - SOL:
facile à remarquer que CQT et CSP sont semblable on a donc:  et <CQT=<SPC implique <TQR=<SPR et donc pour montrer que les deux triangle ont la même surface ,il suffit de montrer que  et donc il suffite de montrer que :  notons O le centre du cercle circonscrit ,on a donc 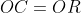 et donc <OCQ=<ORP,et on a deja <OPR=CQO , et puisque OPQ=<CQT=<OQP alors 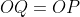 d'ou  et donc QC=PR .CQFD ps : dans ma solution ,j'ai supposé que C,Q,P sont dans cet ordre ,l'autre cas se traite de la même façon .
Dernière édition par boubou math le Dim 16 Juin 2013, 15:42, édité 3 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 15:24 Dim 16 Juin 2013, 15:24 | |
| EXO 3: Trouver toutes les fonction :  :tels que pour tous m,n entier naturel : )/(f(m)^2+n)) | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 16:25 Dim 16 Juin 2013, 16:25 | |
| SOL EX3)
P(m,n):f(m)²+n=k(m²+f(n))
P(0.0):f(0)²=kf(0)
Si f(0)=0 alors P(m,0)donne f(m)=mracine k en remplacant dans l equation initiale on trouve que k=1 donc f(m)=m est bien une solution
si f(0)=/=0
alors k=f(0)
donc P(0,n):f(0)²+n=f(0)(f(n))
f(n)=f(0)+1/f(0)xn
en remplacant dans l equation initial avec k=1 on trouve que m(f(0)^3-1)-2f(0)²=0
pour tout m donc f(0) admet deux valeurs ce qui est absurde donc f(0)=0 donc l identité est la seule solution sauf erreur | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 16:51 Dim 16 Juin 2013, 16:51 | |
| Solution de l'exercice 3 m²+f(n) | f(m)² +n pour m=n=1 1+f(1) |f(1)²+1 a partir d'ici f(1)=1 ou f(1)=0 si f(1)=0 alors 1+f(n) |n pour n=p alors alors f(p) = p-1 pour tout premier p si m=n=p on voit dans l'EF initiale que la relation n'est pas satisfaite pour tout premier p ainsi si f(1)=1 alors 1+f(n) |n+1 alors f(p-1)=p-1 pour tout premier p dans l'EF initiale pour m=p-1 on (p-1)²+f(n) |(p-1)²+n ainsi n >= f(n) (*) pour n= p-1 on a m²+p-1 | f(m)² +p-1 ainsi f(m)² >= m² et puisque f est défini de IN vers IN alors f(n) >= n pour tout entier naturelle n conclusion f(n) =n  | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 16:59 Dim 16 Juin 2013, 16:59 | |
| Exercice 4comme j'ai décidé d'éviter une inégalité monstrueuse  je propose ce joli exercice trouvez tous les triplets (m,p,q) tels que m est entier naturelle et p ,q deux nombres premiers satisfaisant  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 17:15 Dim 16 Juin 2013, 17:15 | |
| - Citation :
- Citation :
- comment tu as abouti à k=1 ?? et je pense qu'on ne peut pas remplacé k =1 vers la fin puisque k est dépendant de n et m .
amigo-6
SOL EX3)
P(m,n):f(m)²+n=k(m²+f(n))
P(0.0):f(0)²=kf(0)
Si f(0)=0 alors P(m,0)donne f(m)=mracine k en remplacant dans l equation initiale on trouve que k=1 donc f(m)=m est bien une solution
si f(0)=/=0
alors k=f(0)
donc P(0,n):f(0)²+n=f(0)(f(n))
f(n)=f(0)+1/f(0)xn
en remplacant dans l equation initial avec k=1 on trouve que m(f(0)^3-1)-2f(0)²=0
pour tout m donc f(0) admet deux valeurs ce qui est absurde donc f(0)=0 donc l identité est la seule solution sauf erreur | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 17:55 Dim 16 Juin 2013, 17:55 | |
| [url=<a] =a&space;\\&space;pour&space;\&space;m=n=1&space;\&space;on&space;\&space;a&space;\&space;\&space;a+1/a^{2}+1=&space;(a-1)(a+1)+2\Rightarrow&space;a+1/2&space;\\&space;donc&space;\&space;a=1&space;\&space;ou&space;\&space;a=0&space;\&space;,&space;\&space;mais&space;\&space;ce&space;\&space;dernier&space;\&space;cas&space;\&space;conduit&space;\&space;a&space;\&space;une&space;\&space;contradiction&space;\\&space;puisque&space;\&space;l'equation&space;fonctionnelle&space;\&space;nous&space;\&space;donne&space;\&space;que&space;\&space;f(n)\geq&space;n&space;\&space;pour&space;\&space;tout&space;\&space;n&space;\\&space;Or&space;\&space;a=1&space;\&space;implique&space;\&space;si&space;\&space;on&space;\&space;remplace&space;\&space;(n;m)&space;\&space;par&space;\&space;(0;1)&space;f(0)&space;+&space;1&space;/&space;1&space;\&space;donc&space;\&space;f(0)=0&space;\\&space;maintenant&space;\&space;si&space;\&space;on&space;\&space;remplace&space;\&space;d'une&space;\&space;part&space;\&space;n&space;\&space;par&space;\&space;0&space;\&space;et&space;\&space;d'autre&space;\&space;part&space;\&space;m&space;\&space;par&space;0&space;\&space;on&space;\&space;a&space;\&space;f(m)=m&space;\&space;pour&space;\&space;tout\&space;m&space;.&space;\\) [/url] | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 18:11 Dim 16 Juin 2013, 18:11 | |
| SOLUTION pour exo 4: - SOL:
l’équation est équivalente à S) d'ou  , on écrit  avec k entier naturel inférieure ou égale à m et a entier naturel impair (il est bien connue que tous nombre entier naturel peut s’écrire sous cette forme d'une façon unique) on a donc  et on à  d'ou a divise p et donc a=1 ou a=p ou a=p² . cas a=1 :  et puisque S est impaire alors m=k ,d'ou l'equation initial s'ecrit : ^4+....+1)\Leftrightarrow&space;p^2-1=(2^m+1)^4+....+(2^m+1)) ,et donc pour m>=3 p²=5[8] donc forcement m=0 , m=1 ,ou m=2 et donc q=2 ou q=3 ou q=5 ,on examine ces cas et on trouve que p=11,m=1,q=3 est la seul solution. cas a=pon remplace dans l’équation initial : on trouve que  et donc  et S étant impair on aura  et donc m=<k mais puisque k=<m alors k=m et donc q-1=p d'ou q=3 et p=2 mais aucune valeur de m n'est valable dans ce cas CAS a=p²l’équation s’écrit  cette dernière équation n'admet évidement aucune solution entière. Conclusion : p=11,m=1,q=3 sont les seuls solution (sauf erreur)
Dernière édition par boubou math le Dim 16 Juin 2013, 23:08, édité 2 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 18:50 Dim 16 Juin 2013, 18:50 | |
| (q^{4}+q^{3}+q^{2}+q+1)\\&space;il&space;\&space;est&space;\&space;clair&space;\&space;que&space;\&space;q&space;\&space;est&space;\&space;impaire&space;\&space;pour&space;\&space;m&space;\geq&space;1&space;\&space;d'ou&space;\&space;q^{4}+q^{3}+q^{2}+q+1&space;est&space;\&space;impaire&space;\&space;est&space;\&space;q-1&space;\&space;est&space;\&space;paire\\&space;puisque&space;\&space;q\geq&space;1&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;2^{m}=q-1&space;\&space;et&space;\&space;que&space;\&space;q^{4}+q^{3}+q^{2}+q+1=p^{2}&space;\\) " &space;\&space;est&space;\&space;solution&space;\&space;ssi&space;\&space;(x;-y)&space;\&space;l'est&space;\&space;aussi&space;.&space;\\&space;on&space;\&space;peut&space;\&space;supposer&space;\&space;donc&space;\&space;que&space;\&space;y\geq&space;0&space;\\&space;on&space;\&space;a&space;\&space;l'equivalence&space;\&space;entre&space;\&space;x^{4}+x^{3}+x^{2}+x+1=y^{2}&space;\\&space;et&space;\&space;\&space;(2x^{2}+x)^{2}&space;+&space;\left&space;(&space;3x^{2}+4x+4&space;\right&space;)=\left&space;(&space;2y&space;\right&space;)^{2}&space;\&space;\left&space;(&space;1&space;\right&space;)&space;\\&space;(2x^{2}+x+1)^{2}-(x-3)(x+1)=(2y)^{2}&space;\&space;\left&space;(&space;1&space;\right&space;)&space;\\&space;Notons&space;\&space;que&space;\&space;3x^{2}+4x+4>&space;0&space;\&space;et&space;\&space;2x^{2}+x+1&space;>&space;0&space;.\\) " / &space;\&space;et&space;\&space;2y>&space;2x^{2}+x+1&space;\&space;par&space;\&space;\left&space;(&space;2&space;\right&space;)&space;\&space;impossible&space;.\&space;de&space;\&space;meme&space;\&space;lorsque&space;\&space;x<&space;-1&space;.&space;\\&space;Finalement&space;\&space;pour&space;\&space;les&space;\&space;valeurs&space;\&space;-1;0;1;2;3&space;\&space;un&space;\&space;calcule&space;\&space;simple&space;\&space;montre&space;\&space;que&space;\&space;\left&space;(&space;x;y&space;\right&space;)&space;=&space;(-1&space;;1&space;);(&space;0;&space;1);(&space;3;11&space;);(3&space;;-11&space;)&space;\\&space;d'ou&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;(p&space;;&space;q&space;;&space;m)=(&space;2;3;1&space;)\) Conclusion (p;q;m)=(11;3;1)
Dernière édition par aymas le Dim 16 Juin 2013, 19:05, édité 3 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 18:54 Dim 16 Juin 2013, 18:54 | |
| si m=0 par un raisonnement semblable on ne trouve aucune solutions .
OOOooof | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 18:58 Dim 16 Juin 2013, 18:58 | |
| je propose l'exercice suivant Exercice 5trouver toutes les fonctions de R* vers R* tel que)=\frac{f(xy)}{f(x)}+f(f(x)))
Dernière édition par aymas le Dim 16 Juin 2013, 22:54, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 19:11 Dim 16 Juin 2013, 19:11 | |
| Boubou math je pense qu'il y aune faute dans ta solution .  alors il te reste le cas a=p² et je pense que tu as commis une faute lors de la reciproque puisque la solution est (11;3;1) et non (11;3;2) | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 21:14 Dim 16 Juin 2013, 21:14 | |
| re les amis  ,pour la démostration d'aymas l'étape ou on doit chercher les entiers q tels que q^4+q^3+q^2+q+1 =p² n'est qu'un Shortlist 91 , Bravo Aymas  | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 22:36 Dim 16 Juin 2013, 22:36 | |
| Solution de l' exercice 5 - Spoiler:
Dernière édition par aymas le Dim 16 Juin 2013, 22:54, édité 2 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 22:36 Dim 16 Juin 2013, 22:36 | |
| a vous de propose un autre exercice | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 | |
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 16 Juin 2013, 23:54 Dim 16 Juin 2013, 23:54 | |
| EXO 6 : Soit a,b,c des réel positifs tels que a+b+c=3,Prouver que :
Dernière édition par boubou math le Lun 17 Juin 2013, 13:52, édité 2 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon Sujet: Re: Marathon  | |
| |
|
  | |
| | Marathon |  |
|
