| | Marathon |  |
|
+12galillee56 younesmath2012 Humber Oty somat BTBICL aymas amigo-6 Top-Math alidos boubou math Yassirkirua 16 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 23 Juin 2013, 22:34 Dim 23 Juin 2013, 22:34 | |
|
Dernière édition par Mehdi.O le Lun 24 Juin 2013, 00:04, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 23 Juin 2013, 23:09 Dim 23 Juin 2013, 23:09 | |
| oui Merci Mehdi tu as raison , deja mon erreur (celle qui ma poussé a poursuivre la suite de ma démarche) est dans cette ligne f(1)=f(1f(1)) >= 0 (j'ai pas fait fait attention je pensais a f(f(1))=f(1) , sa m'apprendra a utilisé un brouillon ) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 23 Juin 2013, 23:20 Dim 23 Juin 2013, 23:20 | |
| Problème 18 :
Trouver toutes les fonctions définie de Z vers lui même qui vérifient la condition suivantes :
pour tout entier m et n (qui ne sont pas forcément distinct )
pgcd(m,n) divise f(m)+f(n) . | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 23 Juin 2013, 23:59 Dim 23 Juin 2013, 23:59 | |
|
Dernière édition par aymas le Lun 24 Juin 2013, 03:33, édité 5 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 | |
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 00:55 Lun 24 Juin 2013, 00:55 | |
| Puisque je vois que vous etes interesse par les equations fonctionnelles voici l'exercice suivant. Exercice 19-x)=2x)
Et j'aimerais bien propose une amelioration a l'exercice propose par Oty (facultative mais on aimerais egalement voir vos belles solutions .) \wedge&space;f(n)&space;\&space;divise&space;\&space;mn+f(mn)&space;\\) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 10:59 Lun 24 Juin 2013, 10:59 | |
| - aymas a écrit:
- Puisque je vois que vous etes interesse par les equations fonctionnelles voici l'exercice suivant.
Exercice 19
-x)=2x)
ma solution , comme f est définie sur R+* on a f(x)-x > 0 on pose : g(x)=f(x)-x > 0 l’équation devient )+g(x)-2x=0) soit u_{n} la suite des itéré de g on a 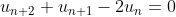 ce qui donne ^{n}) et donc : =a-2b&space;=>&space;b=\frac{x-g(x)}{3},&space;a=\frac{2x+g(x)}{3}) donc ^{n}}u_{n}=\frac{a}{(-2)^{n}}+b) ce qui donne : comme u_{n} >= 0 ^{2n}}\leq&space;b\leq&space;\frac{-a}{(-2)^{2n+1}}) en faisant tendre n vers l'infinie on obtient b=0 et par suite : g(x)=x pour tout x > 0 => f(x)=2x pour tout x > 0 qui est bien solution . sauf erreur . | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 11:03 Lun 24 Juin 2013, 11:03 | |
| Ma solution pour exo 17: - SOL:
-(1) f est injective Soit a,b des réel tels que f(a)=f(b) :f(bf(b))=b^2) :f(af(a))=a^2) :f(af(b))+f(bf(a))=2ab) On combine les trois relation , on trouve que (a-b)²=0 d'ou a=b -(2) f(1)=1 ou f(1)=-1:f(xf(x))=x^2) ,1):f(f(1)^2)+f(f(f(1)))=2f(1)) et on d’après ce qui précède f(f(1))=1 on obtient donc : ,1):f(f(1)^2)=f(1)) d'ou f(1)²=1 d'ou f(1)=1 ou f(1)=-1. On a f(0) et f injective donc =0&space;\Leftrightarrow&space;x=0) d'ou pour tous x réel non nul ,\frac{1}{x}):f(xf(x)f(\frac{1}{x}))+f(\frac{1}{x}f(xf(x)))=2f(x)\Leftrightarrow&space;f(xf(x)f(\frac{1}{x}))+f(x)=2f(x)\Leftrightarrow&space;f(xf(x)f(\frac{1}{x}))=f(x)\Leftrightarrow&space;f(\frac{1}{x})=\frac{1}{f(x)}) =f(xf(\frac{1}{x}))+f(\frac{f(x)}{x})=2\Leftrightarrow&space;f(\frac{x}{f(x)})+\frac{1}{f(\frac{x}{f(x)})}=2) la dernier équation est équivalente à : )=1) si f(1)=1 si f(1)=1et donc f(x)=x pour tous x non nul , et puisque f(0)=0 alors f=id si f(1)=-1de même on trouve f(x)=-id
Dernière édition par boubou math le Lun 24 Juin 2013, 13:13, édité 2 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 11:03 Lun 24 Juin 2013, 11:03 | |
| maxime mea culpa pour le retard j'avais pas mis ma preuve la derniere fois la surjectivite mais vous y etes arrive moi j'ai fais autrement 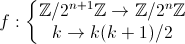 si f(x)=f(y0 alors x=y ou x+y+1=0 dans Z/2^nZ chaque element ademt au plus 2 antecedent et en considerant le cardinal on se rend que chaque element admet exactement 2 antecedent pour l exo 19 j'ai fais la meme solution que oty mais il a ete plus rapide ^^ | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 11:08 Lun 24 Juin 2013, 11:08 | |
| - aymas a écrit:
Et j'aimerais bien propose une amelioration a l'exercice propose par Oty (facultative mais on aimerais egalement voir vos belles solutions .)
Merci aymas , j'avais proposé cette exercice juste parce qu'il etait tres abordable pour qu'il y ait plus de participation du coté des membres du forum , | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 | |
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 12:01 Lun 24 Juin 2013, 12:01 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 12:16 Lun 24 Juin 2013, 12:16 | |
| j'ai remarque que personne n'avait poster d'exo de combinatoire du coup je me permet de poster celui la:
exo 21:
Dans une suite finie de nombre reels la somme de sept terme consecutifs quelconques est negative et la somme de onze termes consecutifs quelconques est positif. determiner le nombre maximum de terme de la suite. | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 14:05 Lun 24 Juin 2013, 14:05 | |
| &space;\&space;et&space;\&space;x&space;\&space;on&space;\&space;le&space;\&space;meme&space;\&space;signe&space;.\\&space;Puisque&space;\&space;f&space;\&space;est&space;\&space;surjective&space;\&space;\exists&space;u&space;\&space;tel&space;\&space;que&space;\&space;f(u)=x&space;\\&space;Remplacant&space;\&space;ce&space;\&space;resultat&space;\&space;on&space;\&space;trouve&space;\&space;que&space;\&space;f(\frac{x+f(x)}{2})=x&space;\\&space;Or&space;\&space;on&space;\&space;trouve&space;\&space;facilement&space;\&space;que&space;\&space;f(x^{2})=2xf(x)-x^{2}&space;\\&space;D'ou&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;f(\left&space;(\frac{x+f(x)}{2}&space;\right&space;)^{2})=x^{2}&space;\\&space;Afin&space;\&space;de&space;\&space;conclure&space;\&space;que&space;\&space;f&space;\&space;est&space;\&space;positive&space;\&space;sur&space;\&space;R+&space;\&space;il&space;\&space;suffit&space;\&space;de&space;\&space;montrer&space;\&space;que&space;\\&space;g(x)=x+f(x)&space;\&space;est&space;\&space;surjective&space;\\&space;Plus&space;\&space;que&space;\&space;ca&space;\&space;on&space;\&space;montre&space;\&space;que&space;\&space;g&space;\&space;est&space;\&space;une&space;\&space;bijection&space;\&space;de&space;\&space;R&space;\&space;vers&space;\&space;R&space;\.&space;Soit&space;\&space;y&space;\&space;de&space;\&space;R&space;\&space;et&space;\&space;x&space;\&space;de&space;\&space;R&space;\.&space;On&space;\&space;a&space;\\&space;g(x)=y\Leftrightarrow&space;\frac{x+f(x)}{2}=\frac{y}{2}\Leftrightarrow&space;f(\left&space;(\frac{x+f(x)}{2}&space;\right&space;))=f(\frac{y}{2})\Leftrightarrow&space;x&space;=f(\frac{y}{2})&space;D'ou&space;\&space;la&space;\&space;conclusion&space;\\.) " /> | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 24 Juin 2013, 20:04 Lun 24 Juin 2013, 20:04 | |
| Pour l'exo 21
je pense que les inegalites sont strictes puisque sinon on prend une suite nulle
d'onc il y a de maximum dans ce cas . les indices ne sont pas majores
Dernière édition par aymas le Lun 24 Juin 2013, 20:09, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 25 Juin 2013, 22:47 Mar 25 Juin 2013, 22:47 | |
| EXO:21- SOL:
Soit n le nombre de terme d'une suite _{n\geq&space;1}) qui satisfait les conditions du problème On va prouver que si 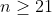 alors une telle suite n'existe pas On a : 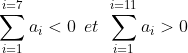 d'ou 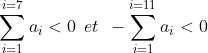 et donc si on fait la somme : 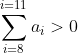 de la même façon : 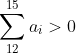 d'ou : 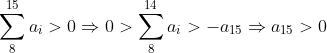 de la même façon on prouve que : 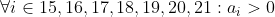 d'ou: 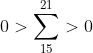 .absurde Il ne reste plus que trouver une suite avec 20 terme qui satisfait les conditions .
| |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 25 Juin 2013, 22:53 Mar 25 Juin 2013, 22:53 | |
| EXO 22:
Soit ABC un triangle aigu avec D, E, F les pieds des altitudes situées sur BC, AC, BC respectivement. L'un des points d'intersection de la ligne EF et le cercle circonscrit est P, les lignes BP et DF rencontrent au point Q prouver: AP = AQ | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 25 Juin 2013, 23:32 Mar 25 Juin 2013, 23:32 | |
| - boubou math a écrit:
- EXO:21
- SOL:
Soit n le nombre de terme d'une suite _{n\geq&space;1}) qui satisfait les conditions du problème On va prouver que si 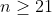 alors une telle suite n'existe pas On a : 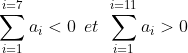 d'ou 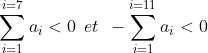 et donc si on fait la somme : 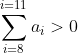 de la même façon : 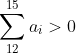 d'ou : 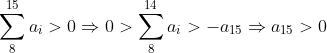 de la même façon on prouve que : 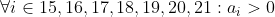 d'ou: 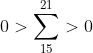 .absurde Il ne reste plus que trouver une suite avec 20 terme qui satisfait les conditions .
je ne suis pas du tout d'accord avec vous Boubou maths  mais en sommant les termes on se rend compte qu ils sont positifs et negatif donc ca ne peut depasser 16 et il existe une suite de terme qui verifie cela bon apres il faut la trouver | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 25 Juin 2013, 23:46 Mar 25 Juin 2013, 23:46 | |
| Tu as tout a fait raison Galilee 56 . mais je pense que Boubou math avait le bon raisonnement . On tout cas je pose ma solution pour l'exercice 22&space;\\&space;=\angle&space;AME&space;\\&space;=&space;\angle&space;AFE&space;(AFME&space;cyclique)&space;\\&space;afin&space;\&space;de&space;\&space;conclure&space;\&space;il&space;\&space;suffit&space;\&space;de&space;\&space;montrer&space;\&space;que&space;\&space;AFQP&space;\&space;est&space;\&space;cyclique&space;.\\&space;On&space;\&space;a&space;\&space;\angle&space;AFQ&space;=&space;180&space;-&space;\angle&space;BFD&space;\\&space;=&space;180&space;-\angle&space;BMD&space;\\&space;=&space;180&space;-&space;\angle&space;AME&space;\\&space;=&space;180&space;-\angle&space;AFE&space;\\&space;=&space;180&space;-&space;\angle&space;APQ&space;\&space;d'ou&space;\&space;la&space;\&space;conclusion&space;\\)

Dernière édition par aymas le Mer 26 Juin 2013, 00:24, édité 3 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 25 Juin 2013, 23:48 Mar 25 Juin 2013, 23:48 | |
| a vous de propose un nouveau exercice | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mer 26 Juin 2013, 00:08 Mer 26 Juin 2013, 00:08 | |
| - galillee56 a écrit:
- boubou math a écrit:
- EXO:21
- SOL:
Soit n le nombre de terme d'une suite _{n\geq&space;1}) qui satisfait les conditions du problème On va prouver que si 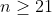 alors une telle suite n'existe pas On a : 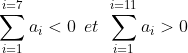 d'ou 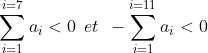 et donc si on fait la somme : 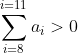 de la même façon : 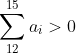 d'ou : 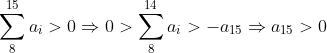 de la même façon on prouve que : 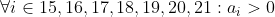 d'ou: 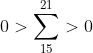 .absurde Il ne reste plus que trouver une suite avec 20 terme qui satisfait les conditions .
je ne suis pas du tout d'accord avec vous Boubou maths

mais en sommant les termes on se rend compte qu ils sont positifs et negatif donc ca ne peut depasser 16
et il existe une suite de terme qui verifie cela bon apres il faut la trouver Mon raisonnement était juste et comme j'avais dit ,il fallait trouver une suite qui satisfait cela pour finir la solution chose que je n'ai pas fait   ,mais il s'est avéré qu'il y a une meilleur majoration , il ne reste plus que chercher une suite cette fois . | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mer 26 Juin 2013, 00:37 Mer 26 Juin 2013, 00:37 | |
| Oui le raisonnement est bon c est juste qu il a dit qu il existe une suite a 20 je paris juste qu il s est trompe en calculant mais le raisonnement est nickel bien joue | |
|
  | |
BTBICL
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 28
Date d'inscription : 25/08/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mer 26 Juin 2013, 02:06 Mer 26 Juin 2013, 02:06 | |
| tonsina homom l watani:  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Ven 28 Juin 2013, 16:44 Ven 28 Juin 2013, 16:44 | |
| - BTBICL a écrit:
- tonsina homom l watani:
 Je propose une solution (qui doit être numéroté 23): On note: 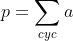 , 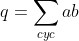 et 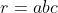 . On a selon l'inégalitré arithmético-géométrique: (c+a)\le(a+p)^2) , et deux autres inégalités similaires. Par conséquent, on aura: ^2}\le\sum_{cyc}\frac{1}{4(a+b)(c+a)}=\sum_{cyc}\frac{b+c}{4(a+b)(b+c)(c+a)}) . Soit donc: ^2}\le\frac{2p}{4(a+b)(b+c)(c+a)}) . Il suffit donc de prouver que (b+c)(c+a)}\le\frac{3}{16}) . Soit encore }\le\frac{3}{16}) ou bien ) .==>(1). La condition donnée s'écrit: 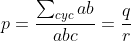 , d'où 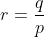 . En reportant dans 1, on trouve qu'il suffit encore de prouver: 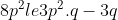 .==>(2) On a aussi d'après l'inégalité de Caushy-Schwartz: ^2) , donc 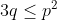 . Donc 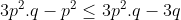 . Ainsi, pour prouver 2, il suffit de montrer que 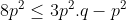 ce qui se réduit à 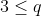 . Or, on a d'après l'inégalité de Caushy-Schwartz: ^2) , donc 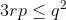 ou encore 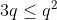 , ce qui donne: 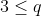 . L'égalité a lieu si et seulement si 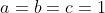 . CQFD. Sauf erreurs. | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Ven 28 Juin 2013, 17:19 Ven 28 Juin 2013, 17:19 | |
| l'exercice de Mr BTBICL n'est qu'un Shortlist 2009 Exercice 24soit (a,b,c) des réels positifs prouver que  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon Sujet: Re: Marathon  | |
| |
|
  | |
| | Marathon |  |
|
