| | Marathon |  |
|
+12galillee56 younesmath2012 Humber Oty somat BTBICL aymas amigo-6 Top-Math alidos boubou math Yassirkirua 16 participants |
|
| Auteur | Message |
|---|
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 12:45 Lun 17 Juin 2013, 12:45 | |
| oui tu as raison j'ai oublier de l'indique
pour montrer que f est impaire on a d'apres ce qui preced pour tout x de R*
f(x+1)=-f(-x)+1
f(x+1)=f(x)+1
on comparant ces deux resultats on obtient que f est impaire d'ou la conclusion | |
|
  | |
BTBICL
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 28
Date d'inscription : 25/08/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 13:59 Lun 17 Juin 2013, 13:59 | |
| ex 6
l'inég. est équivalente à sigma ab²/(1+b²) =< 3/2
d'après iag il sufit de prouver que sigma ab²/(2b)=<3/2 or
sigma ab²/(2b) = 1/2 sigma a = 3/2 donc c fini | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 14:04 Lun 17 Juin 2013, 14:04 | |
| Bien ,à toi de proposer un exercice . | |
|
  | |
BTBICL
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 28
Date d'inscription : 25/08/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 14:13 Lun 17 Juin 2013, 14:13 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 18:26 Lun 17 Juin 2013, 18:26 | |
| Solution de l'exercice 7- Spoiler:
Dernière édition par aymas le Lun 17 Juin 2013, 20:56, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 18:26 Lun 17 Juin 2013, 18:26 | |
| a vous de proposer un autre exercice
Dernière édition par aymas le Lun 17 Juin 2013, 23:35, édité 2 fois | |
|
  | |
somat
Débutant
 Nombre de messages : 3 Nombre de messages : 3
Age : 29
Date d'inscription : 24/02/2012
 | |
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 20:29 Lun 17 Juin 2013, 20:29 | |
| je pense que j'ai aboutit a une solution pour l'exercice 8- Spoiler:
Soit   le cercle circonscrit de ABC et S le projete orthogonal de P sur (BC). D'apres le theoreme de Simson les points Q ;R;S sont alignes sur une droite   . et soit M et N les points d'intersection de la hauteur issue de A dans ABC avec respectivement  et  ; et soit D le point d'intersection de  avec (PS). Puisque A;N;P;D sont cocycliques et (AN) et (DP) sont paralleles on trouve facilement que  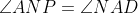 OR puisque (A;D;C;P) et (S;C;R;P) sont cocycliques une petite chasse au angle montre que (AD) et  sont paralleles d'ou  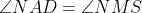 . Et puisque et (MN) et (SP) sont paralleles le trapeze MNPS est isocele. donc PM=SN . Or puisque le point symetrique de H par rapport a (BC) appartient a  ce dernier point est N. on deduit que SN=SH. Ainsi SH=PM et le triangle HSN est isocele en S. D'ou puisque MNPS est isocele. On en deduit que (SH) et (PM) sont paralleles. Et puisque (MH) et (PS) sont paralleles puisqu'ils sont toutes les deux orthogonales a (BC) on deduit que HMPS est un parallelogrames. d'ou la conclusion .
Dernière édition par aymas le Lun 17 Juin 2013, 20:54, édité 2 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 20:34 Lun 17 Juin 2013, 20:34 | |
|
Dernière édition par aymas le Lun 17 Juin 2013, 23:35, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 21:24 Lun 17 Juin 2013, 21:24 | |
| Solution du problème 8 - SOL:
On résout l'exercice dans le plan complexe muni du cercle circonscrit à ABC comme étant le cercle unitaire .on appelle l'affixe d'un point X par x Lemme(1): un point Z appartient à (AB) si et seulement si : z-(a-b)\bar{z}+a\bar{b}+\bar{a}b=0) Lemme(2) Lemme(2)Soit M un point du plan, Z appartient à la droit qui passe par M et perpendiculaire à (AB) si et seulement si : z+(a-b)\bar{z}-m(\bar{a}-\bar{b})-\bar{m}(a-b)=0) on utilisant les deux lemme on trouve que : ) ) On utilisant le Lemme 2 trois fois sur les cotée du triangle ABC,on trouve que 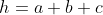 On a d'une part \Leftrightarrow&space;\frac{m-p}{m-h}=\frac{\bar{m}-\bar{p}}{\bar{m}-\bar{h}}&space;\Leftrightarrow&space;\frac{m-p}{m-(a+b+c)}=\frac{\bar{m}-\frac{1}{p}}{\bar{m}-(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})}\Leftrightarrow&space;m(\frac{1}{p}-(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}))+\bar{m}(a+b+c-p)+p(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})-\frac{1}{p}(a+b+c)=0) Et d'autre part : \Leftrightarrow&space;\frac{q-r}{q-m}=\frac{\bar{q}-\bar{r}}{\bar{q}-\bar{m}}\Leftrightarrow&space;\frac{q-r}{q-m}=\frac{1}{2}.\frac{\bar{b}-\bar{c}-\bar{a}p(\bar{b}-\bar{c})}{\bar{q}-\bar{m}}\Leftrightarrow&space;\frac{q-r}{q-m}=&space;\frac{1}{2}.\frac{(\bar{b}-\bar{c})(1-p\bar{a})}{\bar{q}-\bar{m}}\Leftrightarrow&space;\frac{(b-c)(1-a\bar{p})}{q-m}=\frac{(\bar{b}-\bar{c})(1-\bar{a}p)}{\bar{q}-\bar{m}}\Leftrightarrow&space;\frac{(b-c)(p-a)}{p(q-m)}=\frac{(c-b)(a-p)}{pabc(\bar{q}-\bar{m})}\Leftrightarrow&space;(q-m)=abc(\bar{q}-\bar{m})) Si on combine les deux relation ,on peut finalement isoler m , on trouve que 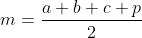 .fin ps: la preuve des deux lemme se fait facilement si on tient en compte le fait que 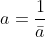
Dernière édition par boubou math le Mar 18 Juin 2013, 10:34, édité 4 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 17 Juin 2013, 21:43 Lun 17 Juin 2013, 21:43 | |
| Exercice 9Soit  n une suite de reels strictement positifs telle que pour tout  * U²n+1 = Un + 1Montrer que la suite  n contient des termes irrationnels. | |
|
  | |
Yassirkirua
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 27
Date d'inscription : 03/02/2013
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 10:53 Mar 18 Juin 2013, 10:53 | |
| e  ON UTILISONS: IAG 3 fois rac(x/(Z+1)(X+1))<1/2 (X/(X+1)+1/(Z+1) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 12:03 Mar 18 Juin 2013, 12:03 | |
| salut , l'exo 9 me parait bien intéressant voici une tentative de résolution : tout d'abord d'aprés l'equation on a : u_{n} > 1 . on suppose par l'absurde que tout les termes de la suites sont des rationnels positives . on peux donc écrire u_{n}=a_{n}\b_{n} , avec a_{n} ^ b_{n}=1 , on remplace dans l’équation on obtient : =a^{2}_{n+1}&space;b_{n}) pour tout n dans N* or comme an et bn sont premier entre eux on a bien bn | b²_{n+1} et b²_{n+1}|bn donc on a : ^{\frac{1}{2^{n}}}) qui doit être un entiers pour tout n dans N* , en faisant tendre n a l'infinie on obtient ; b_{n+1}=1 pour tout n > p . (car comme b_{n} est une suites d'entiers naturels qui converges elle est stationnaire ) , et par conséquent u_{n} appartient a N* pour tout n > p , ce qui induit a u_{n}>= 2 , pour tout n > p . AINSI on obtient une suite strictement décroissante d'entier strictement positif ce qui est impossible ( U_{n+1} < u_{n} dans ce cas )
Dernière édition par Oty le Jeu 04 Juil 2013, 11:19, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 | |
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 15:16 Mar 18 Juin 2013, 15:16 | |
| Salut,
Sur quoi est-ce que vous vous focalisez le plus pour la préparation ? | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 15:30 Mar 18 Juin 2013, 15:30 | |
| Désolé pour l'absence chers amis ....... Exercice 10 Montrer que pour tout réel (a,b,c,d) 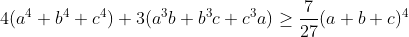 | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 16:39 Mar 18 Juin 2013, 16:39 | |
| Solution de l'exercice 10- Spoiler:
Dernière édition par aymas le Mar 18 Juin 2013, 16:58, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 16:40 Mar 18 Juin 2013, 16:40 | |
| a vous de proposer un nouveau exercice | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 17:11 Mar 18 Juin 2013, 17:11 | |
| EX11
Determinez les fonctions f:]-1;+inf[ -->]-1;+inf[ qui verifient
1) pour tous reels x,y >-1 f(x+f(y)+xf(y))=y+f(x)+yf(x)
2)la fonction x-->f(x)/x est strictement croissante sur ]-1;0[ et sur R+* | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 19:48 Mar 18 Juin 2013, 19:48 | |
| Solution pour l'exo 11- Spoiler:
| |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 20:02 Mar 18 Juin 2013, 20:02 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 20:43 Mar 18 Juin 2013, 20:43 | |
| ma solution pour l'exo 12 :
sa vient de l'identité : 2LHS=(1-a)(1-b)(1-c)+(1+a)(1+b)(1+c) >= 0 . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 | |
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 23:25 Mar 18 Juin 2013, 23:25 | |
| distinguons 3 cas p=103 ca donne modulo p 102=0 mod 103 impossible si 103<p on p|103 (fermat) impossible donc p<103 donc on a ceci 103-E(103/p)=0 mod p p=2,3 | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 18 Juin 2013, 23:30 Mar 18 Juin 2013, 23:30 | |
| n enfants sont assis en cercle. Dolpha donne un bonbon au premier
enfant, saute le second, donne un bonbon au troisieme, saute les deux suivants, donne un
bonbon au prochain enfant, puis saute les trois suivants, et ainsi de suite. Pour quelle valeur
de n, tous les enfants auront-ils au moins un bonbon au bout d’un certain nombre de tours ? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon Sujet: Re: Marathon  | |
| |
|
  | |
| | Marathon |  |
|
