Marathon

Solution de l'exercice 13 (une approche générale )

Spoiler:

Solution de l'exercice 13
Marathon - Page 3 974965_1386605834886766_942656222_n

Marathon - Page 3 975584_1386603918220291_158798023_n

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

L'exercice 14 est resté trop longtemps sans solution
Je propose un autre exo
exo15:
Trouver toutes les fonction 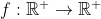$Marathon - Page 3 Gif$ tels que pour tous réels positifs (x,y)
$Marathon - Page 3 Gif$

Solution exercice 15

Spoiler:

Pour l'exercice 14 j'ai trouver une solution dont le principe est de montrer qu'on ne peut pas definir une application surjective f d'un ensemble A vers f(A) tel que f(A) soit un system residue modulo n pour des valeurs de n supérieur stictement a 2 donc il reste de verifier les cas n=1 et n=2 qui sont bien une solution.
Qu'est ce que tu pense Gallilee56 apropos de cette solution .

Exercice 16
(a) Prouver que $Marathon - Page 3 F4eedf95007caab5355c1a6f6c299ae42abcefd6$ est un entier pour $Marathon - Page 3 856d831311a96a37375cbc067d92fda74d64769c$

(b) soit $Marathon - Page 3 13fbd79c3d390e5d6585a21e11ff5ec1970cff0c$ un entier positive, determiner le plus petit entier positive $Marathon - Page 3 F135ebdc8e8df9d9935e50b12e9c50e74fa5b19f$ tel que
$Marathon - Page 3 D06587028b02a3c60e18cac3bd2ecd911d32db06$ est entier pour tout $Marathon - Page 3 41d2cfeb517b0c7eb66501f06411067f4dccd845$

Bonjour mr aymas c ca l idee exactement il faut montrer que pour un certain un n f(k)=k(k+1)/2 est surjective sur z/nz je suis d accord c un peu compliquer c des olympiade de moscou je pense que vous etes sur la bonne piste essayer de creuser en fait n est un puissace de 2 je metterai la solution ce soir

MERCI pour ta reponse je vais essayer un peu a le resoudre tout de suite

Ce que j'ai trouver jusqu'a ce moment
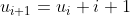Soit $Marathon - Page 3 Gif$ la place de l'enfant n (les indices sont considere modulo n )
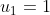Il est clair que le choix des enfants verifie la relations reccurente suivant $Marathon - Page 3 Gif$
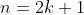et on choisit $Marathon - Page 3 Gif$ . On trouve donc que $Marathon - Page 3 Gif$
Alors pour que le problem, soit verifier il suffit que la fonction
$Marathon - Page 3 N\mathbb{Z}$
Pour une premiere constation cela n'est pas verifier si n est impaire puisque
Posons $Marathon - Page 3 Gif$ on a $Marathon - Page 3 Gif$ mod n ce qui n'est pas permit puisque si $Marathon - Page 3 N\mathbb{Z}$ alors tout les images de f doivent avoir des restes modulo n differentes.
Maintenant on va raisonner sur les premiers qui divise n .
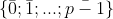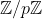soit p un diviseur premier de n . Alors d'apres la construction de f il est clair qu'elle doit verifie aussi une surjection de $Marathon - Page 3 Gif.latex?\left&space;\{&space;\bar{0};\bar{1};..$ " vers $Marathon - Page 3 P\mathbb{Z}$ par le meme argument précédant p doit etre paire
d'ou p=2
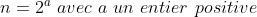alors n est de la forme $Marathon - Page 3 Gif$
Il suffit maintenant monter que n une puissance de 2 resout le problem .

aymas a écrit:: Ce que j'ai trouver jusqu'a ce moment
Soit $Marathon - Page 3 Gif$ la place de l'enfant n (les indices sont considere modulo n )
Il est clair que le choix des enfants verifie la relations reccurente suivant $Marathon - Page 3 Gif$
et on choisit $Marathon - Page 3 Gif$ . On trouve donc que $Marathon - Page 3 Gif$
Alors pour que le problem, soit verifier il suffit que la fonction
$Marathon - Page 3 N\mathbb{Z}$
Pour une premiere constation cela n'est pas verifier si n est impaire puisque
Posons $Marathon - Page 3 Gif$ on a $Marathon - Page 3 Gif$ mod n ce qui n'est pas permit puisque si $Marathon - Page 3 N\mathbb{Z}$ alors tout les images de f doivent avoir des restes modulo n differentes.
Maintenant on va raisonner sur les premiers qui divise n .
soit p un diviseur premier de n . Alors d'apres la construction de f il est clair qu'elle doit verifie aussi une surjection de $Marathon - Page 3 Gif.latex?\left&space;\{&space;\bar{0};\bar{1};..$ " vers $Marathon - Page 3 P\mathbb{Z}$ par le meme argument précédant p doit etre paire
d'ou p=2
alors n est de la forme $Marathon - Page 3 Gif$
Il suffit maintenant monter que n une puissance de 2 resout le problem .

@aymas ce qui est en rouge n'est pas claire , il faut une preuve .

dsl pour le retard j'etais un peu deborder hier voila
on voit facilement que le k enfant qui recoit un bonbon est congrue k(k+1)/2 modulo n montrons que l application est surjective si et seulement n est une puissance de 2
premiere implication:soit p un nombre premier divisant n et different de 2 donc tout les residu modulo sont atteint soit c tel 2c=1 mod p donc k(k+1)/2=ck(k+1) mod p si k= 0,-1 mod p on atteindra jamais donc restera sans bonbon (ce qui est dommage) donc p est forcement paire p=2 n=2^n
apres il faut verifier que cela marche
c la meme idee que ayamas
Marathon - Page 3 Codeco22

et prouver que c'est surjectif
PS: bien joue Mr ayamas Very Happy

aymas a écrit:: $Marathon - Page 3 P\mathbb{Z}&space;\&space;on&space;\&space;un&space;\&space;antecedant&space;\\&space;par&space;\&space;f&space;\&space;dans&space;\&space;\left&space;\{&space;0;1;..;n-1&space;\right&space;\}&space;\&space;et&space;\&space;puisque&space;\&space;on&space;\&space;travail&space;\&space;mod&space;p&space;\&space;\&space;et&space;\&space;n\geq&space;p&space;\\&space;on&space;\&space;peut&space;\&space;toujours&space;\&space;limite&space;\&space;l'ensemble&space;\&space;de&space;\&space;depart&space;\&space;pour&space;\&space;les&space;\&space;valeurs&space;\left&space;\{&space;0;1.$

désolé aymas mais je ne vois pas que ceci est une preuve que f ''doit"" etre une surjection de Z\pZ => Z\pZ ,
en faite je pense que l'argument de que pour montrer que n est une puissance de 2 , le fait que f(p-1)=f(0)mod p , n'est pas suffisant a part si tu prouve que f doit vraiment etre une surjection de Z\pZ vers Z\pZ ,
sinon il faut prouver que f(p-1)=f(0) ''mod n '' et non mod p c'est pas pareil .

galillee56 a écrit:: dsl pour le retard j'etais un peu deborder hier voila
on voit facilement que le k enfant qui recoit un bonbon est congrue k(k+1)/2 modulo n montrons que l application est surjective si et seulement n est une puissance de 2
premiere implication:soit p un nombre premier divisant n et different de 2 donc tout les residu modulo sont atteint soit c tel 2c=1 mod p donc k(k+1)/2=ck(k+1) mod p si k= 0,-1 mod p on atteindra jamais donc restera sans bonbon (ce qui est dommage) donc p est forcement paire p=2 n=2^n
apres il faut verifier que cela marche
c la meme idee que ayamas

et prouver que c'est surjectif
PS: bien joue Mr ayamas

et ou est la preuve Mr Galillee 56 ? et pourquoi tu as choisie Z\2^{n+1}Z comme ensemble de depart ?

Oty je pense que ce que tu veut dire apropos de la surjectivite est prouve .
Sinon il parait que je n'ai pas bien saisie ce que tu veux dire. amicalement.

aymas a écrit:: Oty je pense que ce que tu veut dire apropos de la surjectivite est prouve .
Sinon il parait que je n'ai pas bien saisie ce que tu veux dire. amicalement.

ce que je veux dire aymas , c'est quand tu travaille modulo p c'est que tu considère p enfants qui sont parmis c'est n enfant , j'entends dire que par exemple n=24 on a prenant p=2 l'application est sujerctif pour c'est 2 enfants mais pas pour les 24 enfants , donc il te faut impérativement prouvé que que f est belle est bien surjectif de Z\pZ => Z\pZ avec p premier , en effet en supposant qu'elle est surjectif dans Z\nZ => Z\nZ , tout élément Z\nZ admet un antécédent et comme p est un diviseur de n alors Z\pZ est inclus dans Z\nZ donc toute élément de Z\pZ admettent eux aussi des antécédents , il reste a prouvé que c'est antécédant appartiennent a Z\pZ , pour pouvoir affirmé que c'est f est aussi surjective de Z\pZ => Z\pZ , quand tu dis par définissions de f qu'entends tu dire par cela ? merci
me concernant j'avais prévu d'essayer ce probleme durant ce weekend inchallah .
en tout cas tres interessant probleme .
amicalement .

galillee56 a écrit:: n enfants sont assis en cercle. Dolpha donne un bonbon au premier
enfant, saute le second, donne un bonbon au troisieme, saute les deux suivants, donne un
bonbon au prochain enfant, puis saute les trois suivants, et ainsi de suite. Pour quelle valeur
de n, tous les enfants auront-ils au moins un bonbon au bout d’un certain nombre de tours ?

on numérote les enfants de 1 à n
Il s'agit de montrer que :
n est une puissance de 2 <==> pour k de 1 à n, l'équation : k+tn=s(s+1)/2 admet au moins une solution (t,s) dans N² ( t+1= nombre de tours)

exercice 14 :
on numérote les enfants de 1 a n .

[img]http://latex.codecogs.com/gif.latex?on~~pose~~a_{k}~~le~~numero~~de~~l'enfant~~ayant~~recu~~le~~bonbon~~on~~\\a_{1}=1~~a_{2}=a_{1}+2=3,~~a_{3}=a_{2}+3=6,~~par~~suite~~on~~a~~a_{k}\equiv&space;a_{k-1}+k&space;[n].&space;\\il~~s'agit~~que~~la~~suite~~a_{k}~~&space;prenne~~toute~~~les~~valeurs~~de~~l'ensemble~~\\&space;\{0,1,..,n-1\}.\\on~~pose~~f(k)=\frac{k(k+1)}{2},&space;ainsi~~a_{k}\equiv&space;f(k)[n]&space;.&space;\\Considerant~~2~~cas&space;.&space;\\n~~impair&space;,~~on~~a~~f(k+n)\equiv&space;f(k)[n]&space;,~~donc~~on~~a~~seulement~~besoin~~d'etudier~~les~~n~~premiere~~valeurs~~&space;et~~par~~consequant~~la~~suite~~peut~~prendre~~toute~~les~~valeurs~~voulu~~si~~tout~~les~~&space;\\a_{1},a_{2},...a_{n},~~sont~~distincts.~~Mais~~on~~a~~aussi~~f(n-k)\equiv&space;f(k)[n]~~et~~par~~consequent~~il~~y~~a~~au~~plus~~\frac{n+1}{2}~~valeurs~~differente~~\\ce~~qui~~ne~~verifie~~pas~~la~~condition~~demander.\\Maintenant~~si~~n~~est~~pair~~on~~f(k+2n)\equiv&space;f(k)[n]&space;,~~et~~donc~~on~~seulment~~besoin~~de~~regarder~~les~~~2n~~premiere~~valeurs.\\Mais~~f(2n-1-k)\equiv&space;f(k)[n]~~et~~f(2n-1)\equiv&space;0[n][/img]
[img]http://latex.codecogs.com/gif.latex?et~~donc~~la~~suite~~prend~~toute~~les~~valeurs~~si~~a_{1},a_{2},..,a_{n-1}~~&space;prennent~~les~~valeurs~~\\&space;1,2,...,n-1&space;\\on~~peut~~verifier~~en~~testant~~differente~~valeur\\de~~n~~que~~pour~~n=2,4,8,16~~sa~~marche~~ce~~qui~~n'est~~pas~~le~~cas~~pour~~\\n=6,10,12,14~~ce~~qui~~suggere~~que~~n~~doit~~etre~~une~~puissance~~de~~2.\\On~~suppose~~n~~une~~puissance~~de~~2.\\supposant~~qu'il~~existe~~0<s<r<n~~tel~~que~~\\&space;f(r)\equiv&space;f(s)[n]\Rightarrow&space;(r-s)(r+s+1)\equiv&space;0[n].~~puisque~~les~~deux~~facteurs~~sont~~inferieur~~strictement~~a~~n~~~tout~~les~~deux~~ne~~peuvent\\etre~~divisible~~par~~n~~et~~donc~~il~~sont~~forcement~~tout~~les~~deux~~pair~~ce~~qui~~est~~impossible~~car~~leur~~somme~~est~~\\2r+1&space;(il~~n'ont~~pas~~la~~meme~~parite).~~et~~donc~~l'application~~f~~est~~injective~~pour~~\\[[1,n-1]],~~ainsi~~f(1),f(2),...,f(n-1)~~sont~~des~~restes~~differents~~modulo~~n~~reste~~a~~prouver~~qu'ils~~ne~~peuvent~~etre~~0~~modulo~~n~~\\ce~~qui~~est~~vrai~~car~~2n~~ne~~peut~~pas~~diviser~~r(r+1)[/img]
[img]http://latex.codecogs.com/gif.latex?pour~~0<r<n~~et~~donc~~n~~ne~~peut~~pas~~diviser~~f(r)~~par~~le~~meme~~argument~~precedent~~et~~donc~~f(1),f(2),...,f(n),prennent~~&space;toute~~&space;les~~&space;valeurs~~\\1,2,...,n-1&space;~~et~~donc~~toute~~les~~puissances~~de~~2~~marchent.&space;\\Maintenant~~soit~~n~~une~~solution~~au~~probleme~~et~~m~~un~~diviseur~~de~~n~~si\\f(k)\equiv&space;a[n]\Rightarrow&space;f(k)\equiv&space;a[m]~~donc~~m~~est~~aussi~~une~~solution.&space;\\comme~~on~~a~~deja~~montrer~~que~~les~~nombres~~impair~~ne~~sont~~pas~~solutions~~au~~probleme~~\\il~~s'ensuit~~que~~n~~doit~~etre~~une~~puissance~~de~~2[/img]

sauf erreur .

Oty j'ai essayer de lire ta preuve et il me parait que tu fais la meme preuve que la mienne sauf que tu as monter que f doit etre injective de Z/nZ vers Z/nZ ce qui est trivial puisque tout application surjective d'un ensemble fini vers lui est une injection . Or comme tu l'as dis n est solution et m diviseur n alors m est solution et c'est ca ce que j'ai voulu dire lorsque j'ai parler de la definition de f . de plus il me parait que lorsque tu as etudier l'ensemble des diviseur de n il te suffit de travailler sur un diviseur premier de n est montrer qu'il ne peut pas etre que 2 ce qui est fait dans ma preuve .
Mais on ce qui concerne la verfication que pour n puissance de 2 on atteint notre objective il me parait que c'est bon .
mais on tout cas bonne solution .
note: la preuve n'ai pas lisible (directement) . il te faut la réécrire .

on aimerait egalement que quelqu'un repond a la question que j'ai propose a fin qu'on puisse continuer ce marathon . Sinon je peut la changer . j'attend la confirmation des membres .

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

Exo 17 :
Trouver toutes les fonctions f :IR---->IR ,tels que :
$Marathon - Page 3 Gif$

boubou math a écrit:: Exo 17 :
Trouver toutes les fonctions f :IR---->IR ,tels que :
$Marathon - Page 3 Gif$

Edit : solution fausse ....

Oty a écrit:

boubou math a écrit:: Exo 17 :
Trouver toutes les fonctions f :IR---->IR ,tels que :
$Marathon - Page 3 Gif$

jolie problème , voici ma solution
x=y=0 => f(0)=0 .
x=1 , y, => f(f(y))+f(yf(1))=2y pour tout y (T)
x=y=1 , f(f(1))=1 .
x= y=f(1)=> f(1)²=1
x=y => f(xf(x))=x² >=0 pour tout x
donc f(1)=f(1.f(1)) >= 0 => f(1)=1 .
donc (T) devient
f(f(y))+f(y)=2y pour tout y dans R .
soit u_n la suite des itéré de f , f^{0) (x)=x u_{1}=f(x) , u_{n+1)=f(u_{n})
on a d’après la relation précédente
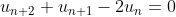
$Marathon - Page 3 Gif$
l'equation caractéristique est :
r²+r-2=0 => r1=-2 et r2=1 ;
donc
$Marathon - Page 3 Gif$
ce qui donne :
$Marathon - Page 3 Gif$
or toujour d'apres la relation (T) on a f est injective et donc strictement monotones et par conséquent u_{n} est strictement monotone ceci
est possible si et seulement si b=0 ce qui donne f(x)=x quelque soit x dans R , qui vérifie bien l'equation
sauf erreur .

Pour que f inj => f st monotone soit vraie, il faut que f soit continue, et même si on suppose que f est st monotone, on a pas nécessairement u_n st monotone, il suffit de prendre une involution ( par ex: x-> a-x )

» Marathon
» Marathon
» MARATHON (un peu de géo)
» Marathon De Géométrie
» Marathon de combinatoire