| | Marathon |  |
|
+12galillee56 younesmath2012 Humber Oty somat BTBICL aymas amigo-6 Top-Math alidos boubou math Yassirkirua 16 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 29 Juin 2013, 12:50 Sam 29 Juin 2013, 12:50 | |
| - alidos a écrit:
- l'exercice de Mr BTBICL n'est qu'un Shortlist 2009
Exercice 24
soit (a,b,c) des réels positifs prouver que
 Je propose une approche que j'espère être juste: L'inégalité proposée s'écrit: +\frac{1+\frac{b}{c}+\frac{c}{a}+\frac{a}{b}}{1+\frac{a}{c}+\frac{b}{a}+\frac{c}{b}}\ge7) . On pose:  ,  et  . On a: 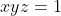 . On pose encore: 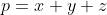 , 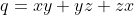 . L'inégalité devient: +\frac{1+x+y+z}{1+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\ge7) . Ou encore: }+\frac{1}{x(1+z)}+\frac{1}{y(1+x)}\bigg)+\frac{1+p}{1+q}\ge7) . Soit (1+x)}{\prod_{cyc}(1+x)}\bigg)+\frac{1+p}{1+q}\ge7) ou bien  . Et ainsi:  . On pose  . L'inégalité devient:  , soit après simplification: \ge 2pq+4q+3q^2) . On a:  , il suffit donc de montrer que: \ge 4q(1+q)) ou bien  . Je n'ai pas pus démontrer ce résultat, mais j'ai pensé à une chose: puisque l'ingalité de départ est homogène, on peut supposer une contrainte sur les variables initiales, ce qui va faciliter la tâche... Sauf erreurs. | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 | |
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Dim 30 Juin 2013, 18:23 Dim 30 Juin 2013, 18:23 | |
| continue...  | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 11:26 Lun 01 Juil 2013, 11:26 | |
| - younesmath2012 a écrit:
- exercise 25:
 Je propose une solution: Vu l'homogénité de l'inégalité, on peut supposer que: 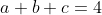 . L'inégalité proposée s'écrit  ou encore ((a-b)^2+(b-c)^2+(c-a)^2)\le4abc) après factorisation. Ou bien ^2+(b-c)^2+(c-a)^2\le abc) après simplification. Mais, l'inégalité est symétrique: on peut donc supposer que  . On a  [  ], donc  et ainsi: ^2\le|a-b|) et de même pour les autres. D'où: ^2+(b-c)^2+(c-a)^2\le |a-b|+|b-c|+|c-a|=a-b+b-c+a-c=2(a-c)) . Et il reste à démontrer que: \le abc) ou encore \le 2c) . Cela est vrai, car:  et  découle du fait que ) (  et  ). Le cas d'égalité est bien évidemment: =(2,1,1)) en plus des permutation, vu la symétrie du problème. Sauf erreurs. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 11:31 Lun 01 Juil 2013, 11:31 | |
| Je propose un nouveau problème: Problème 26:Soit 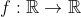 une fonction qui vérifie: \in\mathbb{R}^2):|f(x+y)+\sin{(x)}+\sin{(y)}|\le2) . Montrez que: :|f(x)|\le1+\cos{(x)}) . Bonne chance.
Dernière édition par nmo le Lun 01 Juil 2013, 15:11, édité 1 fois | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 15:04 Lun 01 Juil 2013, 15:04 | |
| est ce que vous etes sur Mr''nmo'' que c'est juste ? car si oui on aura  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 15:13 Lun 01 Juil 2013, 15:13 | |
| - younesmath2012 a écrit:
- est ce que vous etes sur Mr''nmo'' que c'est juste ?
car si oui on aura  Oui, je suis sûr de l'énoncé. Tu peux vérifier ici: http://www.artofproblemsolving.com/Forum/viewtopic.php?f=38&t=541208. | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 18:00 Lun 01 Juil 2013, 18:00 | |
| Je propose ma solution pour Problème 26:+sin(x)+sin(y)&space;\right&space;|\leq&space;2&space;\\&space;\Leftrightarrow&space;-2\leq&space;f(x+y)+sin(x)+sin(y)\leq&space;2&space;\\&space;Soit&space;\&space;P(x,y)&space;\&space;l'assertion&space;\&space;de&space;\&space;cette&space;\&space;derniere&space;\&space;inegalite&space;\\&space;On&space;\&space;a&space;\&space;P(x,-y)&space;\&space;on&space;\&space;a&space;\&space;-2\leq&space;f(x-y)+sin(x)-sin(y)\leq&space;2&space;\\&space;or&space;\&space;on&space;\&space;remplacant&space;\&space;(x,y)&space;\&space;par&space;\&space;(\frac{pi}{2}+x,\frac{pi}{2}+y)&space;\&space;dans&space;\&space;cette&space;\&space;derniere&space;\&space;inegalite&space;\&space;on&space;\&space;a&space;\\&space;-2\leq&space;f(x-y)+cos(x)-cos(y)\leq&space;2&space;\\&space;pour&space;\&space;y=0&space;\&space;dans&space;\&space;cette&space;\&space;relation&space;\&space;on&space;\&space;a&space;\&space;f(x)\geq&space;-1-cos(x)&space;\&space;pour&space;\&space;tout&space;\&space;x&space;\\&space;pour&space;\&space;x=0&space;\&space;et&space;\&space;y\rightarrow&space;-x&space;\&space;on&space;\&space;a&space;\&space;f(x)\leq&space;1+cos(x)&space;\&space;pour&space;\&space;tout&space;\&space;x&space;\\&space;D'ou&space;\&space;la&space;\&space;conclusion) | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 18:02 Lun 01 Juil 2013, 18:02 | |
| a vous de propose un nouveau exercice | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 18:03 Lun 01 Juil 2013, 18:03 | |
| qqs x,y dans R, |f(x)|=<2-|sin(x-y)+sin(y)|=2-2|sin(x/2)cos(x/2-y)|
on pose g(y)=2-2|sin(x/2)cos(x/2-y)|
Montrer que g(y)=<1+cos(x) | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 18:09 Lun 01 Juil 2013, 18:09 | |
| Je pense que le resultat que vous avez propose Mr abdelbaki.attioui est faux prend y=x/2+pi/2
donc ce que vous propose est equivalent a 1=<cos(x) pour tout x ce qui est clairement faux | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 18:45 Lun 01 Juil 2013, 18:45 | |
| Je propose un problème, qui est plus difficile: Problème 27:Soit  un entier. Déterminez toutes les fonctions 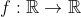 qui satisfont: \in\mathbb{R}*^2): f(x^k.y^k)=x.y.f(x).f(y)) et =0) . Bonne chance.P.S: Une autre solution du problème 26 est proposée dans le site déjà cité. | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 22:33 Lun 01 Juil 2013, 22:33 | |
| Je propose ma solution pour l'exercice 24&space;\&space;l'assertion&space;\&space;de&space;\&space;l'equation&space;\&space;fonctionnelle&space;\&space;f(x^{k}y^{k})=xyf(x)f(y)&space;\\&space;P(1,1)&space;\Rightarrow&space;\&space;f(1)=1&space;\&space;ou&space;\&space;f(1)=0&space;\\&space;1-&space;\&space;Si&space;\&space;f(1)=0&space;\\&space;P(x,1)&space;\&space;f(x^{k})=0&space;\\&space;P(x,x)&space;\&space;f(x)=0&space;\&space;pour&space;\&space;tout&space;\&space;x&space;\\&space;2-&space;\&space;Si&space;\&space;f(1)=1&space;\\&space;P(x,1)&space;\&space;f(x^{k})=xf(x)&space;\\&space;D'ou&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;f(xy)=f(x)f(y)&space;\&space;pour&space;\&space;tout&space;\&space;x&space;\&space;et&space;\&space;y&space;\\&space;On&space;\&space;suppose&space;\&space;que&space;\&space;\exists&space;a&space;\neq&space;0&space;\&space;tel&space;\&space;que&space;\&space;f(a)=0&space;\\&space;on&space;\&space;remplacant&space;\&space;(x,y)&space;\&space;par&space;\&space;(\frac{x}{a},a)&space;\&space;dans&space;\&space;cette&space;\&space;derniere&space;\&space;relation&space;\&space;on&space;\&space;a&space;\\&space;f(x)=0&space;\&space;pour&space;\&space;tout&space;\&space;x&space;\&space;contradiction&space;\&space;.&space;\&space;donc&space;\&space;f(x)=0\Leftrightarrow&space;x=0&space;\\) [img]http://latex.codecogs.com/gif.latex?On&space;\&space;prouve&space;\&space;facilement&space;\&space;par&space;\&space;reccurence&space;\&space;que&space;\&space;f(x^{k})=f(x)^{k}&space;\\&space;Donc&space;\&space;P(x,1)&space;\&space;implique&space;\&space;que&space;\&space;f(x^{k})=xf(x)&space;\\&space;Par&space;\&space;la&space;\&space;remarque&space;\&space;precedante&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;f(x)^{k-1}=x&space;\&space;et&space;\&space;f(x^{k-1})=x&space;\&space;et&space;\&space;f(x^{k-1})=f(x)^{k-1}&space;\\&space;D'ou&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;k&space;\&space;doit&space;\&space;etre&space;\&space;paire&space;\&space;puisque&space;\&space;x&space;\leq&space;0&space;\Rightarrow&space;\&space;f(x)^{k-1}\leq&space;0&space;\\&space;Maintenant&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\\&space;f(x)=\sqrt[k-1]{x}&space;\&space;si&space;\&space;x\geq&space;0&space;\\&space;f(x)=-\sqrt[k-1]{-x}&space;\&space;si&space;\&space;x&space;\leq&space;0&space;\\&space;Synthese&space;:&space;\&space;les&space;\&space;solutions&space;\&space;sont&space;\\&space;f(x)=\sqrt[k-1]{x}&space;\&space;si&space;\&space;x\geq&space;0&space;\\&space;f(x)=-\sqrt[k-1]{-x}&space;\&space;si&space;\&space;x&space;\leq&space;0\\&space;et&space;\&space;f(x)=0&space;\&space;pour&space;\&space;tout&space;\&space;x[/img]
Dernière édition par aymas le Lun 01 Juil 2013, 23:01, édité 3 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 01 Juil 2013, 22:57 Lun 01 Juil 2013, 22:57 | |
| a vous de proposer un nouveau exercice | |
|
  | |
Yassirkirua
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 27
Date d'inscription : 03/02/2013
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 02 Juil 2013, 00:37 Mar 02 Juil 2013, 00:37 | |
|
Dernière édition par Yassirkirua le Mar 02 Juil 2013, 00:57, édité 1 fois | |
|
  | |
Yassirkirua
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 27
Date d'inscription : 03/02/2013
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 02 Juil 2013, 00:40 Mar 02 Juil 2013, 00:40 | |
|
Dernière édition par Yassirkirua le Mar 02 Juil 2013, 00:57, édité 1 fois | |
|
  | |
Yassirkirua
Habitué
 Nombre de messages : 16 Nombre de messages : 16
Age : 27
Date d'inscription : 03/02/2013
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 02 Juil 2013, 00:53 Mar 02 Juil 2013, 00:53 | |
| [[img]<a href="http://www.codecogs.com/eqnedit.php?latex=\[&space;\frac{a}{b^2+1}+\frac{b}{c^2+1}+\frac{c}{a^2+1}\geq\frac{3}{4}(a\sqrt{a}+b\sqrt{b}+c\sqrt{c})^2&space;\]\sum" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\[&space;\frac{a}{b^2+1}+\frac{b}{c^2+1}+\frac{c}{a^2+1}\geq\frac{3}{4}(a\sqrt{a}+b\sqrt{b}+c\sqrt{c})^2&space;\]\sum" title="\[ \frac{a}{b^2+1}+\frac{b}{c^2+1}+\frac{c}{a^2+1}\geq\frac{3}{4}(a\sqrt{a}+b\sqrt{b}+c\sqrt{c})^2 \]\sum" /></a>[/img] | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 02 Juil 2013, 00:55 Mar 02 Juil 2013, 00:55 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Mar 02 Juil 2013, 00:59 Mar 02 Juil 2013, 00:59 | |
| a vous de proposer un nouveau exercice
| |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 20 Juil 2013, 16:29 Sam 20 Juil 2013, 16:29 | |
| - younesmath2012 a écrit:
- probleme 29:
 Voici une démarche à suivre lorsqu'il faut profiter de l'outil informatique: On pose 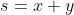 et 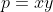 . On a ^2=x^2+y^2+2xy=x^2+y^2+2p) , donc  . On a encore: ^3=x^3+y^3+3xy(x+y)=x^3+y^3+3ps) , donc  . On a finalement ^2=(x^2+y^2)^2=(s^2-2p)^2) , donc  . La condition initiale devient alors:  . Qui s'écrit encore: +s+s^2+s^3+s^4-8=0) . Vu comme une équation du second degré en p, son discriminent est: ^2-8(s+s^2+s^3+s^4-8 )=8s^4+16s^3+17s^2+4s+68) , qui est strictement positif. (Ces résultats sont confirmé par wolfram alpha). ***Si:  . L'inégalité à démontrer s'écrit:  ou bien  . Ce qui est vrai: http://www.wolframalpha.com/input/?i=s^2+-+s+-+2\left%28\frac{4+s^2-\sqrt{8+s^4%2B16+s^3%2B17+s^2%2B4+s%2B68}%2B3+s%2B2}{4}\right%29+\geq+0 . ***Et si  . L'inégalité à démontrer s'écrit:  ou bien  . Ce qui n'est pas vrai: http://www.wolframalpha.com/input/?i=s^2+-+s+-+2\left%28\frac{4+s^2%2B\sqrt{8+s^4%2B16+s^3%2B17+s^2%2B4+s%2B68}%2B3+s%2B2}{4}\right%29+\geq+0 . Il faut prendre le premier p pour avoir le résultat. Cependant, je ne sais pas pourquoi? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Sam 20 Juil 2013, 16:48 Sam 20 Juil 2013, 16:48 | |
| Je propose un nouveau problème, respectant les règles du jeu: Problème 30:Déterminez tous les fonctions 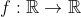 qui satisfont \in\mathbb{R}\times\mathbb{R}):f(x+y)^2=f(x)^2+2f(xy)+f(y)^2) . Bonne chance.P.S: même s'il n'y a plus de membres actifs... | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 29 Juil 2013, 00:56 Lun 29 Juil 2013, 00:56 | |
| Soit P(x,y) l'assertion,
P(x,1/x) donne f(x+1/x)²=f(x)²+2f(1)+f(1/x)² (*)
Soit la fonction Q(x)=f(x)²
L'équation devient Q(x+1/x)=Q(x)+Q(1/x)+2f(1) (**)
On va montrer qu'il n'y a qu'une seule solution f(x)=cx ou Q1(x)=(cx)² et c'est celle qui saute aux yeux dès le premier regard.
Pour cela supposons qu'il en existe une autre et soit la fonction P(x)=Q1(x)-Q2(x)
En soustrayant les deux équations des deux fonctions on obtient : P(x+1/x)=P(x)+P(1/x) ce qui donne P(x)=kx pour tout x avec k dans IR.
Donc Q1(x)=Q2(x)+kx. Ce qui veut dire que l'équation admet au plus deux solutions, ainsi l'autre solution éventuelle pour (**) est Q(x)=cx²+kx, Cependant, en prenant en compte le fait que Q(x)>=0 pour tout x dans IR cette solution n'est plus valable pour (*).
La solution restante est donc f(x)=kx
Résumé : f(x)=kx pour tout k dans IR | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Marathon Sujet: Re: Marathon  Lun 29 Juil 2013, 03:43 Lun 29 Juil 2013, 03:43 | |
| - nmo a écrit:
- Spoiler:
- younesmath2012 a écrit:
- probleme 29:
 Voici une démarche à suivre lorsqu'il faut profiter de l'outil informatique: On pose 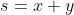 et 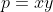 . On a ^2=x^2+y^2+2xy=x^2+y^2+2p) , donc  . On a encore: ^3=x^3+y^3+3xy(x+y)=x^3+y^3+3ps) , donc  . On a finalement ^2=(x^2+y^2)^2=(s^2-2p)^2) , donc  . La condition initiale devient alors:  . Qui s'écrit encore: +s+s^2+s^3+s^4-8=0) . Vu comme une équation du second degré en p, son discriminent est: ^2-8(s+s^2+s^3+s^4-8 )=8s^4+16s^3+17s^2+4s+68) , qui est strictement positif. (Ces résultats sont confirmé par wolfram alpha). ***Si:  . L'inégalité à démontrer s'écrit:  ou bien  . Ce qui est vrai: http://www.wolframalpha.com/input/?i=s^2+-+s+-+2\left%28\frac{4+s^2-\sqrt{8+s^4%2B16+s^3%2B17+s^2%2B4+s%2B68}%2B3+s%2B2}{4}\right%29+\geq+0 . ***Et si  . L'inégalité à démontrer s'écrit:  ou bien  . Ce qui n'est pas vrai: http://www.wolframalpha.com/input/?i=s^2+-+s+-+2\left%28\frac{4+s^2%2B\sqrt{8+s^4%2B16+s^3%2B17+s^2%2B4+s%2B68}%2B3+s%2B2}{4}\right%29+\geq+0 . Il faut prendre le premier p pour avoir le résultat.
Cependant, je ne sais pas pourquoi? C'est parce que 4p =< s² < 2+3s+4s²+racine(...+68) . Ce cas est donc impossible parcequ'il n'y a pas de valeurs de x et y qui satisfont le deuxième " si " | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon Sujet: Re: Marathon  | |
| |
|
  | |
| | Marathon |  |
|
