- younesmath2012 a écrit:
- probleme 29:

Voici une démarche à suivre lorsqu'il faut profiter de l'outil informatique:
On pose
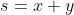
et
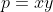
.
On a
^2=x^2+y^2+2xy=x^2+y^2+2p)
, donc

.
On a encore:
^3=x^3+y^3+3xy(x+y)=x^3+y^3+3ps)
, donc

.
On a finalement
^2=(x^2+y^2)^2=(s^2-2p)^2)
, donc

.
La condition initiale devient alors:

.
Qui s'écrit encore:
+s+s^2+s^3+s^4-8=0)
.
Vu comme une équation du second degré en p, son discriminent est:
^2-8(s+s^2+s^3+s^4-8 )=8s^4+16s^3+17s^2+4s+68)
, qui est strictement positif.
(Ces résultats sont confirmé par wolfram alpha).
***Si:

.
L'inégalité à démontrer s'écrit:

ou bien

.
Ce qui est vrai: http://www.wolframalpha.com/input/?i=s^2+-+s+-+2\left%28\frac{4+s^2-\sqrt{8+s^4%2B16+s^3%2B17+s^2%2B4+s%2B68}%2B3+s%2B2}{4}\right%29+\geq+0 .
***Et si

.
L'inégalité à démontrer s'écrit:

ou bien

.
Ce qui n'est pas vrai: http://www.wolframalpha.com/input/?i=s^2+-+s+-+2\left%28\frac{4+s^2%2B\sqrt{8+s^4%2B16+s^3%2B17+s^2%2B4+s%2B68}%2B3+s%2B2}{4}\right%29+\geq+0 .
Il faut prendre le premier p pour avoir le résultat.
