| | Marathon De Géométrie |  |
|
+22Oty SM.OMAR yasserito az360 boubou math momo1729 maths_lady diablo902 ali-mes SarakZit.A King Dijkschneier Bensouda majdouline Mehdi.O darkpseudo Sylphaen Sporovitch MohE nmo extrajijo Mr.Wajih 26 participants |
|
| Auteur | Message |
|---|
az360
Expert grade2
 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
| | Sujet: Re: Marathon De Géométrie Sam 25 Fév 2012, 06:43 | |
| moi je suis avec vous les gars !!!  | |
|
| | |
yasserito
Expert sup
Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
| | Sujet: Re: Marathon De Géométrie Sam 25 Fév 2012, 14:23 | |
| Je suis avec vous, j'essairais de faire de mon mieux..  | |
|
| | |
SM.OMAR
Habitué
Nombre de messages : 16
Age : 29
Date d'inscription : 14/02/2011
| | Sujet: Re: Marathon De Géométrie Sam 25 Fév 2012, 19:14 | |
| je suis avec vous (moi aussi je passerai le deuxieme stage) | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: Marathon De Géométrie Sam 21 Avr 2012, 13:49 | |
| | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Marathon De Géométrie Sam 21 Avr 2012, 22:50 | |
| - Mehdi.O a écrit:
- ali-mes a écrit:
- Je propose ce problème:
Problème 31:
Soit ABC un triangle, considérons le point B' tel que [BB'] est un diamètre dans le cercle circonscrit au triangle ABC, soit I le centre du cercle inscrit au triangle ABC, et M le point de contact du cercle inscrit au triangle ABC avec le côté AC, on construit les points K et L sur les côtés AB et BC respectivement tel que BK=MC et LB=AM.
Montrer que (B'I) et (LK) sont perpendiculaires. J'attends de toi que tu changes le problème, il est erroné. Merc d'avance Je ne pense pas cher Mehdi.O, je t'invite à lire les solutions figurant dans ce lien et ceux dans un lien qui gisait dedans: http://www.artofproblemsolving.com/Forum/viewtopic.php?f=47&t=471777. Je partage avec toi l'idée de le changer, car le jeu est bloqué à cause de ce problème une longue durée. Au plaisir! | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Marathon De Géométrie Sam 21 Avr 2012, 23:43 | |
| Je propose donc un autre problème:
Problème 31':
Considérons un quadrilatère inscriptible ABCD, soient P l'intersection de (AB) et (CD) et Q l'intersection de (AD) et (BC). Les tangentes au cercle circonscrit au quadrilatère ABCD issues du point Q touchent le cercle aux points E et F.
Montrer que P, E et F sont collinéaires. | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: Marathon De Géométrie Lun 23 Avr 2012, 23:43 | |
| Solution au problème 31 :- Spoiler:
Soit O le centre du cercle circonscrit au quadrilatère ABCD et G le point d'intersection des diagonales, d'après un résultat connu les droites OQ et PG sont perpendiculaires, soit X le point d'intersection de FE et OQ, aussi il est clair que FE et OQ sont perpendiculaires et ainsi X est milieu de FE, on suppose que PG intersecte le cercle (ABCD) en une corde E'F' différente de EF, on aura donc X' l'intersetion de F'E' est milieu de ce segment, et ainsi si T est l'intersection de EE' et FF' ( en supposant que l'ordre des points ne change pas puisque la situation est symétrique) on aura T appartient à OQ médiatrice des deux segments EF et E'F', et ainsi on aura TE' et TF' des tangentes à ce cercle, ainsi on a par une chasse d'angle EF' est parallèle à OF et de même pour FE' parallèle à OE, en supposant bien sûr que la corde EF est plus proche à O que E'F', ainsi si E" est l'antipode de E par rapport au cercle (ABCD) on aura les points E"; F et T sont collinéaires et ainsi les points E", F' et F sont collinéaires, mais puisque ces trois points appartiennent au même cercle, on a nécessairement deux de ces points sont confondus. Si E"=F alors EF est diamètre de (ABCD) et ainsi X=O et ainsi les points P, E et F sont trivialement collinéaires. Sinon, on aura F'=F et ainsi par une démonstration similaire on aura E'=E ainsi les points P, E, G et F sont collinéaires. Sauf erreur .
Problème 32 :Soit M le milieu d'un segment BC d'un triangle ABC isocèle AC=AB. Soit X un point dans le petit arc MA du cercle circonscrit au triangle ABM, Soit T un point à l'intérieur de l'angle BMA tel que <TMX=90 et TX=BX. Montrer que <MTB-<MTC ne dépend pas du choix de X. | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Marathon De Géométrie Mar 24 Avr 2012, 22:46 | |
| Solution au problème 32:  Soit Y l'intersection du cercle circonscrit au triangle MTX, avec BT. alors: %20\perp%20(BT)) et puisque le triangle XTB est isocèle, il s'en suit que Y est le mileu de [BT]. Et on a M est le mileu de [BC], donc par la réciperoque de Thalès: (MY) // (CT). D'où:  (Car (MY) // (CT) )  (le quadrilatère TXMY est inscriptible)  (le triangle XBT est isocèle est Y le mileu de [BT], donc (XY) est la bissectrice de angle{TXB})  . CQFD Problème 33:Soit ABCD un parallélogramme. Soient E£[AB], F£[BC], G£[CD], H£[DA] tels que AE = DG, EB = GC, AH = BF, HD = FC. Montrer que (BH)inter(DE), (EG)inter(FH) et C sont alignés. | |
|
| | |
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Marathon De Géométrie Mer 25 Avr 2012, 15:23 | |
| un petit retour , pour proposer ma démo pour le problème 33 : On dénote P l'intersection de BH et DE et Q l'intersection de EG et HF , on a donc les points D , P ,E sont alignés ainsi en appliquant Menelaus au triangle HAB , on a :  (1) , mais il est claire que :  et  On remplace dans (1) on obtient l'égalité qu'il fallait prouver dans le triangle BHF pour conclure une nouvelle fois par Menelaus ... Problème 34 On se donne un quadrilatère ABCD inscrit dans un cercle de diamètre BD . Soit A' et B' les symétrique de A et B par apport a BD et AC respectivement , on dénote P l'intersection de A'C et BD et Q l'intersection de AC et B'D , Démonter que les droite PQ et AC sont perpendiculaire . | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Marathon De Géométrie Mer 25 Avr 2012, 21:47 | |
| Salut, voici ma réponse qui est un peu longue avec beaucoup de trigo  : Solution au problème 35:  Clairement, A' appartient à (C) le cercle circonscrit au quadrilatère ACDB. B' est la symétrique de B par rapport à (AC), donc: \perp%20(AC)) , ainsi il suffit montrer que: \parallel%20(BB%27)) , ce qui est équivalent à démontrer par la réciperoque de Thalès que:  . Soient: \cap%20(BD)) , et \cap%20(AC)) . On a: }{\sin(\angle%20DPC)}\times%20\frac{DC}{DB}) . Et:  .  . Donc: }{\sin(\angle%20BAC-\angle%20ABD)}\times%20\frac{DC}{DB}) }{DB.\sin(\pi%20-%20\angle%20BDC-%20\angle%20ABD)}=\frac{DC.\sin(\angle%20ABD)}{DB.\sin(%20\angle%20BDC+%20\angle%20ABD)}) Et on a: }{DB%27\sin%20(%20\angle%20DQC)}=\frac{DC.\sin(\angle%20DCA)}{(DQ+QB%27)\sin%20(%20\angle%20DQC)}=\frac{DC.\sin(\angle%20DCA)}{DQ.\sin(\angle%20DQC)+QB%27.\sin(\angle%20B_1QB)}) }{DC.\sin(\angle%20DCQ)+QB.\frac{BB_1}{QB}}=\frac{DC.\sin(\angle%20DCA)}{DC.\sin(\angle%20DCA)+BB_1}) ( QB'=QB car Q appartient à la médiatrice de [BB']) }{DC.\sin(\angle%20DCA)+AB.\sin{(\angle%20BAB_1)}}=\frac{DC.\sin(\angle%20ABD)}{DC.\sin(\angle%20ABD)+AB.\sin{(\angle%20BDC)}}) }{DC.\frac{AD}{BD}+AB.\frac{BC}{BD}}=\frac{DC.\sin(\angle%20ABD)}{BD\left%20(\frac{DC}{BD}.\frac{AD}{BD}+\frac{AB}{BD}.\frac{BC}{BD}%20\right%20)}=\frac{DC.\sin(\angle%20ABD)}{BD\left%20(\cos(\angle%20BDC).\sin(\angle%20ABD)+\cos(\angle%20ABD).\sin(\angle%20BDC)%20\right%20)}) }{BD.(\sin(\angle%20ABD+\angle%20BDC)%20)}%20=\frac{DP}{DB}) ... Le résultat en découle immédiatement. Problème 35:Soit (C) un demi cercle de [PQ] son diamètre, un cercle (Gamma) est tangent intérieurement à (C) et à segment [PQ] dans C. Soit (AB) la tangente à (Gamma) et perpendiculaire sur (PQ) tel que A£(C) et B£[CQ]. Montrer que (AC) est la bissectrice de angle{PAB}. | |
|
| | |
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Marathon De Géométrie Mar 15 Mai 2012, 22:40 | |
| je propose ma solution pour le problème 35 , moche mais sa reste une solution ! il suffit de montrer que le triangle AQC est isocèle , pour conclure . on va essayé de montrer que QA=QC , pour ce faire en exprime les deux longueurs en fonctions de paramètre fixe , soit ici R le rayon du grand cercle que je note son centre O , et r le rayon du petit cercle que je note son centre I .On pose :  on a =\frac{IC}{IO}=\frac{r}{R-r}\rightarrow&space;r=\frac{Rsin(\alpha)}{sin(\alpha)+1}) , d'ou cos(\alpha)+R\rightarrow&space;CQ=(1+\frac{cos(\alpha)}{sin(\alpha)+1})R) . Poson maintenant ) , notons que : =\frac{OC-r}{R}=\frac{cos(\alpha)-sin(\alpha)}{1+sin(\alpha)}) ,ce qui nous permet d'exprimé QA en utilisant une des formules de transformation du cosinus (cos(2x)) : +1}{sin(\alpha)+1})) qui est par chance belle est bien le carré de QC d'ou le résultat sauf erreur ... (je posterai un nouveau problème vendredi soir inchallah ) . | |
|
| | |
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Marathon De Géométrie Mer 23 Mai 2012, 01:00 | |
| Problème 36 : soit ABC un triangle est un point D a l’intérieur de celui-ci tel que : <DAC=<DCA=30 et <DBA=60 . soit E le milieu de [BC] . F un point de AC tel que : AF=2FC . Prouver que (DE) et (EF) sont perpendiculaire .
| |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Marathon De Géométrie Dim 27 Mai 2012, 17:38 | |
| Solution problème 36:  Problème 37: soit ABCD un quadrilatère convexe tel que  et  et  .Les diagonales [AC] et [BD] se coupent au point P . Determiner la mesure de l'angle 
Dernière édition par abdelkrim-amine le Lun 02 Juil 2012, 02:03, édité 3 fois | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Marathon De Géométrie Lun 28 Mai 2012, 13:15 | |
| | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Marathon De Géométrie Lun 28 Mai 2012, 14:13 | |
| - ali-mes a écrit:
- @ abdelkrim-amine: Pourriez vous donner la définition des points H et G pour suivre la démo ? Sinon, pour ton problème, il est très connu, et a déjà apparu sur le forum: https://mathsmaroc.jeun.fr/t16954p45-marathon-de-geometrie (Le commentaire de Mohe).
H et G les milieux de [AC] et [CD] respectivement | |
|
| | |
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Marathon De Géométrie Lun 09 Juil 2012, 00:24 | |
| Problème 38 (Proposé par un ami): ABC un triangle, H son orthocentre, M et K sont les milieux de AB et CH. Soit X l'intersection de la bissectrice intérieure de l'angle C^BH et celle de l'angle CÂH. Prouver que X, M et K sont colinéaires.  Bonne chance | |
|
| | |
Geo
Habitué
Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
| | Sujet: Re: Marathon De Géométrie Ven 13 Juil 2012, 13:23 | |
| Solution au probleme 38:- Spoiler:
1)On remarque que H_BHH_AC est inscriptible: XBA + XAB=1/2 (HBC +HAC)+ 180 -AHB= 1/2 (180-2C)+AHH_B =90-C + 90 -CAH=90 donc AXB=90, par conséquent AH_BXH_AB est inscriptible. On a H_BAX=XAH donc arc(XH_B)=arc(XH_A) donc XH_B=XH_A d'une autre part on a MX=MH_B=MH_A d'où (XM) est la médiatrice de [H_BH_A]. 2) Dans le quadrilatère H_BHH_AC (KM) est la ligne de Gauss et (H_BH_A) est la ligne d'Aubert .Il est très connu que la ligne (KM) est perpendiculaire à (H_AH_B) de 1 et 2 on déduit que 
Probleme 39:Soit ABC un triangle, I le centre de son cercle inscrit et F,D et E les projections orthogonales de I sur AB,BC et AC, respectivement.Soit Met N les milieux de BC et BA. Prouver que les droites MN,EF et CI sont concourantes. | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Marathon De Géométrie Ven 13 Juil 2012, 16:38 | |
| - Geo a écrit:
Probleme 39:
Soit ABC un triangle, I le centre de son cercle inscrit et F,D et E les projections orthogonales de I sur AB,BC et AC, respectivement.Soit Met N les milieux de BC et BA. Prouver que les droites MN,EF et CI sont concourantes.  Premièrement , notons que IFBD et IFAE sont inscipribles. Et soit L l'intersection de (CI) et (EF). Ainsi, il suffit montrer que les points L, N et M sont collinéaires. D'après un lemme facilement démontrable (que j'ai déjà posté ici sur le forum , mais je n'arrive pas à trouver son lien ): le pentagone FLBDI est inscriptible. Il suffit montrer que L appartient à (FID): -\frac{\angle%20C}{2}=\pi%20-%20\frac{\pi}{2}-\angle%20IAF-\frac{\angle%20C}{2}=\frac{\pi}{2}-\frac{\angle%20A}{2}-\frac{\angle%20C}{2}=\frac{\angle%20B}{2}=%20\angle%20FBI) . Donc:  .Soit X l'intersection de (BL) et (AC), on a: angle{BLC}=angle{XLC} et angle{LCB}=angle{LCX}, et puisque les deux triangles CLX et CLB ont une base commune, on conclut qu'il sont isométriques, et par conséquence LB=LX , d'où L est le milieu de [BX], et on a: (MN)//(AC), et (LN)//(AX)=(AC), il s'en suit que les points L, N et M sont collinéaires et le résultat en découle... Problème 40:Soient (Gamma_1) et (Gamma_2) deux cercles qui s'intersectent en A et B, (XY) est une droite tangente commune aux deux cercles tel que (XY) est proche de A que B, et X appartient à(Gamma_1) et Y appartient à (Gamma_2). (AX) coupe (Gamma_2) la deuxième fois dans C, et (AY) coupe (Gamma_1) la deuxième fois dans D. On note E=(DX)inter(CY). Montrer que si Q est la deuxième intersection de (ECD) est (EXY), alors angle{QXE}=angle{QBA}. (ECD)=le cercle circonscrit au triangle ECD, et même chose pour (EXY). | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: Marathon De Géométrie Sam 06 Juil 2013, 21:30 | |
| Pour faire revivre ce marathon , je propose ce lien qui contient une solution de ce problemme http://www.artofproblemsolving.com/Forum/viewtopic.php?p=1899886#p1899886
EXO 41
The side BC of the triangle ABC is extended beyond C to D so that CD = BC. The side CA is extended beyond A to E so that AE = 2CA. Prove that, if AD = BE, then the triangle ABC is right-angled.
| |
|
| | |
aymas
Maître
Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
| | Sujet: Re: Marathon De Géométrie Sam 06 Juil 2013, 23:23 | |
| Je propose ma solution pour l'exo 41 &space;\&space;AB^{2}+AD^{2}=2AC^{2}+\frac{1}{2}BD^{2}=2AC^{2}+2BC^{2}&space;\&space;et&space;\\&space;(2)&space;\&space;AB^{2}+AE^{2}=2AH^{2}+\frac{1}{2}BE^{2}\Leftrightarrow&space;AB^{2}+4AC^{2}=\frac{1}{2}AD^{2}+\frac{1}{2}AD^{2}=AD^{2}&space;\\&space;de&space;\&space;(1)&space;\&space;et&space;\&space;(2)&space;\&space;on&space;\&space;deduit&space;\&space;que&space;\&space;AB^{2}+AC^{2}=BC^{2}&space;\&space;CQFD) | |
|
| | |
aymas
Maître
Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
| |
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Marathon De Géométrie Dim 07 Juil 2013, 00:48 | |
| - boubou math a écrit:
- EXO 41
The side BC of the triangle ABC is extended beyond C to D so that CD = BC. The side CA is extended beyond A to E so that AE = 2CA. Prove that, if AD = BE, then the triangle ABC is right-angled. La solution de aymas est correcte, je propose une solution alternative: Supposons que le plan est complexe muni d'un repère orthonormé (B,C,I) (où I est un point d'affixe i), dont l'origine est B d'affixe 0, C d'affixe 1. On suppose que l'affixe de A est x. Il vient immédiatement d'après les hypothèses que l'affixe de D est 2, celui de E est 3x-2. On pose: 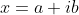 . On suppose qu'on a: 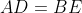 . Il s'ensuit que  , soit  une fois les calculs faits. On a d'autre part: +1=1=BC^2) . On en conclût que le triangle ABC est rectangle en A, par le biais de la réciproque du théorème de phytagore... CQFD. Sauf erreurs. | |
|
| | |
aymas
Maître
Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
| | Sujet: Re: Marathon De Géométrie Dim 07 Juil 2013, 18:45 | |
| Vu que person n'a pu resoudre le problem precedant il parait que je n'ai pas bien choisi l'exercice pour commencer ce marathon donc je vous propose l'exercice suivant Exrcice 43  | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: Marathon De Géométrie Dim 07 Juil 2013, 22:17 | |
| Sol EXO 43Soit E le milieu de [AB] , on veut prouver que FHEB est cocyclique Prenons E comme étant le centre d'un repaire complexe , prenons A(1),B(-1) On a C(c) ,F((c+1)/2) on a \rightarrow&space;-3m=b+2a=1\Rightarrow&space;M(-1/3)) On a H ,A,M aligné d'ou  De même H le pied perpandiculaire de M sur AF d'ou  après on résout le système pour trouver 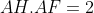 mais on a 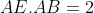 d'ou FHEB est cocyclique on a (FE) // (AC) est donc <ABC=ACB=<FEB=<FHB
Dernière édition par boubou math le Dim 07 Juil 2013, 22:18, édité 1 fois | |
|
| | |
aymas
Maître
Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
| | Sujet: Re: Marathon De Géométrie Dim 07 Juil 2013, 22:17 | |
| je propose ma solution pour l'exo 43&space;\&space;et&space;\&space;(EM)&space;\\&space;on&space;\&space;a&space;\&space;donc&space;\&space;(EM)&space;\&space;parallele&space;\&space;avec&space;\&space;(AC)&space;\\&space;Alors&space;\&space;EMB&space;\&space;est&space;\&space;isocele&space;\&space;donc&space;\&space;EB=EM&space;\\&space;et&space;\on&space;\&space;appliquant&space;\&space;le&space;\&space;theoreme&space;\&space;de&space;\&space;thales&space;\\&space;On&space;\&space;a&space;\&space;\frac{EM}{AC}=\frac{1}{3}=\frac{EF}{FC}=\frac{ED}{AC}&space;\Rightarrow&space;ED=EM&space;\\&space;Donc&space;\&space;ED=EM=EB&space;\&space;alors&space;\&space;le&space;\&space;triangle&space;\&space;DBM&space;\&space;est&space;\&space;rectangle&space;\&space;en&space;\&space;B&space;\&space;d'ou&space;\\&space;\angle&space;DBM&space;=&space;90&space;=\angle&space;DHM&space;\\&space;Alors&space;\&space;les&space;\&space;points&space;\&space;D&space;,&space;B&space;,M,H&space;\&space;sont&space;\&space;cocyclique&space;\&space;donc&space;\&space;on&space;\&space;a&space;\\&space;\angle&space;FHB&space;=&space;\angle&space;EMB&space;=&space;\angle&space;CAB&space;=&space;\angle&space;ABC=\angle&space;FBM) | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Marathon De Géométrie | |
| |
|
| | |
| | Marathon De Géométrie | |
|
