|
| | Marathon De Géométrie |  |
|
+22Oty SM.OMAR yasserito az360 boubou math momo1729 maths_lady diablo902 ali-mes SarakZit.A King Dijkschneier Bensouda majdouline Mehdi.O darkpseudo Sylphaen Sporovitch MohE nmo extrajijo Mr.Wajih 26 participants | |
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 27 Mai 2011, 20:23 Ven 27 Mai 2011, 20:23 | |
| Solution au problème 26:- Spoiler:
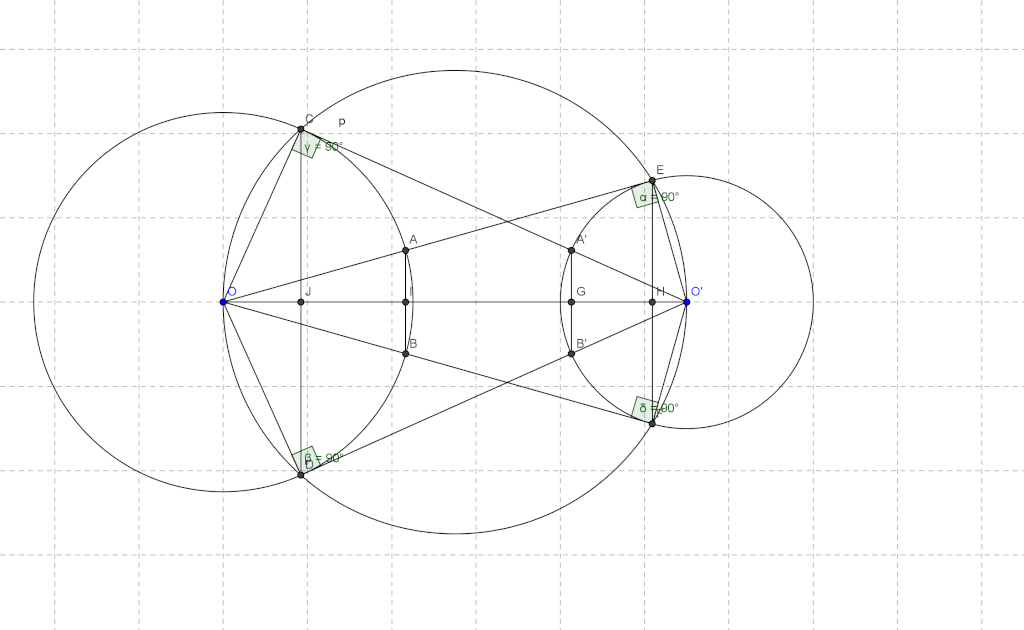 Notons C et D les points d'intersection des tangentes menées par O' avec (C), et E et F les points d'intersection des tangentes menées par O avec (C'). Nous avons clairement l'hexagone OCEO'FD est inscriptible, et que OE=OF et O'C=O'D ( puissance d'un point par rapport à un cerlce). D'autre part par cocylclicité nous avons [OO') est bissectrice de l'angle <EOF, et [O'O) est bissectrice de l'angle <CO'D, et nous avons aussi 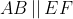 et 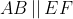 car OAB et O'A'B' sont aussi des triangles isocèles. Ainsi [OO'] est une médiatrice commune des segments [AB],[CD],[A'B'] et [EF] ce qui assure le fait que 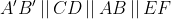 . Notons J,I,G et H les points d'intersections de (OO') avec [CD],[AB],[A'B'] et [EF] respectivement. D'après Thalès il vient que : 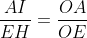 et 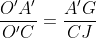 , ce qui donne 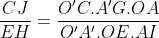 .=> (1)D'autre part, Ptolémée dans les quadrilatères inscriptibles OEO'F et OCO'D nous donne : 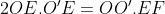 et 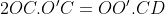 ainsi : 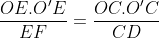 , donc 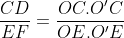 => (2). Et compte tenu du fait que : 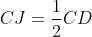 et que 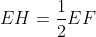 . Donc de (1) et de (2) on conclut que : 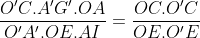 Ainsi : 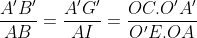 . On pose R et r les rayons des cerlces (C) et (C') respectivement donc : ainsi : 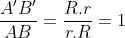 CQFD.
| |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 29 Mai 2011, 16:41 Dim 29 Mai 2011, 16:41 | |
| Problème 27:
Soit ABC un triangle, le centre de son cercle inscrit est I. Les bissectrices [AI) et [BI) et [CI) coupent BC,AC et AB en D et E et F respectivement. La médiatrice de [AD] coupe BI et CI en M et N respectivement. Montrez que les points A,I,M et N sont cocycliques. | |
|   | | Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 29 Mai 2011, 21:24 Dim 29 Mai 2011, 21:24 | |
| Mehdi , Je t'avais dit que Je posterai ma solution au problème 26 :
Il est facile de remarquer que les points (O,O',C,E) et (C,A,A',E) sont cocycliques => angle(EAA')=ang(EOO') => (AA') (OO') et (BB') sont parallèles.
Notons F le point d'intersection de (AA') et (C') => 90=B'EO'+BEO=EB'O'+B'FE ==> [B'F] est un diamètre de (C') => (A'B') et (AA') sont perpendiculaires . et puisque (AB) et (AA') sont aussi perpendiculaires ( on peut la prouver de la meme manière ) ==> (AB) // (A'B') => AA'BB' est un rectangle. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 05 Juil 2011, 16:48 Mar 05 Juil 2011, 16:48 | |
| - Mehdi.O a écrit:
- Problème 27:
Soit ABC un triangle, le centre de son cercle inscrit est I. Les bissectrices [AI) et [BI) et [CI) coupent BC,AC et AB en D et E et F respectivement. La médiatrice de [AD] coupe BI et CI en M et N respectivement. Montrez que les points A,I,M et N sont cocycliques. Ilsemblerait que personne n'a trouvé la solution. Merci de proposer une, si tu l'as. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 05 Juil 2011, 17:37 Mar 05 Juil 2011, 17:37 | |
| Suite à la demande de nmo je pospose la solution du problème 27: Solution au problème 27: Notons M_1 l'intersection du cercle circonscrit de ABD avec [BI), nous avons angle{DAM_1}=angle{M_1BD}=angle{M_1BA}=angle{ADM_1} ce qui implique que AM_1=DM_1, soit M_1 appartient à la médiatrice de [AD], ce qui coincide avec M, ainsi M=M_1 et ainsi le quadrilatère AMDB est inscriptible, de même on trouve que ANDC est inscriptible. Et ainsi : angle{AMI}+angle{ANI}=angle{AMB}+angle{ANC}=angle{ADB}+angle{ADC}=180. Ainsi les points A,N,I et M sont cocycliques. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 05 Juil 2011, 18:51 Mar 05 Juil 2011, 18:51 | |
| - Mehdi.O a écrit:
- Suite à la demande de nmo je pospose la solution du problème 27:
Solution au problème 27:
Notons M_1 l'intersection du cercle circonscrit de ABD avec [BI), nous avons angle{DAM_1}=angle{M_1BD}=angle{M_1BA}=angle{ADM_1} ce qui implique que AM_1=DM_1, soit M_1 appartient à la médiatrice de [AD], ce qui coincide avec M, ainsi M=M_1 et ainsi le quadrilatère AMDB est inscriptible, de même on trouve que ANDC est inscriptible.
Et ainsi : angle{AMI}+angle{ANI}=angle{AMB}+angle{ANC}=angle{ADB}+angle{ADC}=180.
Ainsi les points A,N,I et M sont cocycliques. Très bonne solution. Personnellement, j'ai silloné vainement plusieurs chemins et j'ai gaspillé une très grande durée sans résultats. Encore une fois, merci pour la solution. Je crois que c'est à toi de proposer un nouveau problème. | |
|   | | SarakZit.A
Habitué

 Nombre de messages : 11 Nombre de messages : 11
Age : 57
Localisation : Chine
Date d'inscription : 02/07/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 05 Juil 2011, 18:58 Mar 05 Juil 2011, 18:58 | |
| si Mehdi.O le permé, je propose : Problème 28 :Soit ABC un triangle et soient D et E des points sur [AB] et [AC], respectivement, tels que (DE) soit parallèle à (BC). Soit P un point quelconque intérieur au triangle ADE, et soient F et G les intersections de (DE) avec (BP) et (CP) respectivement. Soit Q la seconde intersection des cercles circonscrits aux triangles PDG et PFE. Prouver que A,P et Q sont colinéaires.  | |
|   | | ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 15 Sep 2011, 22:18 Jeu 15 Sep 2011, 22:18 | |
| Solution au problème 28:- Spoiler:
 On note (C) le cercle circonscrit au triangle PDG, et (C') le cercle circonscrit au triangle PFE. On note H l'intersection de (C) avec la droite (AB), et I l'intersection de (C') avec la droite (AC). Le quadrilatère HDPG est inscriptible donc: <HPC=<HPG=<HDG=180-<ADG=180-<ADE=180-<ABC=180-<HBC. Donc le quadrilatère HPCB est inscriptible, donc H appartient au cercle circonscrit au triangle BPC.Le quadrilatère PIEF est inscriptible donc: <BPI=<FPI=180-<IEF=180-<IED=180-<AED=180-<ACB=180-<ICB. Donc le quadrilatère PICB est inscriptible, donc I appartient au cercle circonscrit au triangle BPC.On conclut que le quadrilatère DICB est inscriptible. On a: <HIE=<HIC=180-<HBC=180-<ABC=180-<ADE=<EDH. Donc le quadrilatère DIEH est inscriptible, on note (C'') son cercle circonscrit. On a donc: (PQ) est l'axe radical de (C) et (C'), la droite (HD)=(AB) est l'axe radical de (C) et (C'') et (IE)=(AC) est l'axe radical de (C') et (C''). Donc d'après la théorème des axes radicaux, les droite (AB), (AC) et (PQ) sont concourantes, et puisques les droite (AB) et (AC) partagent un point A, il s'en suit que Q, P et A sont collinéaires.
Problème 30:Soit ABC un triangle rectangle en A, soit D la projection orthogonale de A sur (BC). La bissectrice de l'angle <BAD coupe le côté [BC] en E. La parallèle à (AE) passant par C coupe (AD) en F. Montrer que (EF) recoupe (AB) en son milieu. | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 18 Oct 2011, 21:41 Mar 18 Oct 2011, 21:41 | |
| | |
|   | | maths_lady
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 29
Localisation : tétouan
Date d'inscription : 11/03/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 10 Nov 2011, 14:27 Jeu 10 Nov 2011, 14:27 | |
|
- ABCD شبه منحرف
- M et N milieux de [CD] et [BC] dans cet ordre
- soit P ta9ato3 (AM) et (DN)
- Montrez que si : AP = 4 PM alors ABCD est un parallélograme.
| |
|   | | momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 12 Nov 2011, 18:33 Sam 12 Nov 2011, 18:33 | |
|
Dernière édition par momo1729 le Dim 01 Avr 2012, 13:15, édité 1 fois | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 12 Nov 2011, 19:01 Sam 12 Nov 2011, 19:01 | |
| Math lady solution posté dans le forum du tronc commun | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 12 Nov 2011, 21:09 Sam 12 Nov 2011, 21:09 | |
| @math-lady : Prière de supprimer ton problème, le problème de ali-mes est encore en jeu. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 12 Nov 2011, 23:43 Sam 12 Nov 2011, 23:43 | |
| Solution au problème 29:- Spoiler:
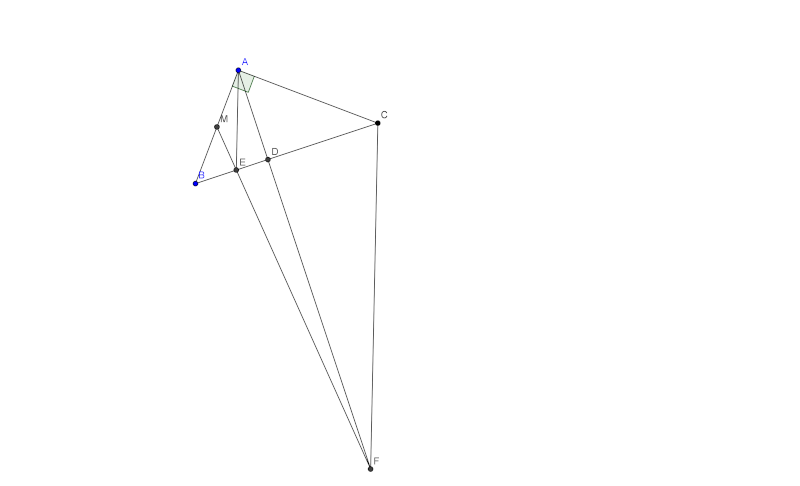 Notons M le point d'intersection de EF avec AB. D'après les données du problème nous avons la collinéarité des points F,E et M. Ainsi en appliquant Ménélaus dans le triangle ABD nous obtenons 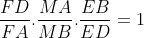 Ainsi on se doit de prouver que MA=MB mais d'après le théorème de la bissectrice intérieur il suffit de prouver que : 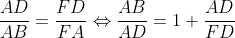 . D'autre part, puisque les deux triangles ADE et DCF sont isométriques nous avons : 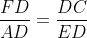 . Maintenant soit  l'angle <EDA. Nous avons : 2(alpha)=<ACB. On pose y=ED.Et ainsi : =\frac{AD}{DC}=tan(2\alpha&space;)=\frac{2tan(\alpha&space;)}{1-tan^{2}(\alpha&space;)}=\frac{2\frac{y}{AD}}{1-\frac{y^2}{AD^2}}=\frac{2y.AD}{AD^2-y^2}) ce qui donne y=ED=AC-DC. Ainsi il suffit de prouver que : 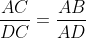 ce qui est vrai puisque les deux triangles ADC et ABC sont isométriques. Sauf erreur 
| |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 13 Nov 2011, 12:14 Dim 13 Nov 2011, 12:14 | |
| - Mehdi.O a écrit:
- Solution au problème 29:
- Spoiler:
 Notons M le point d'intersection de EF avec AB. D'après les données du problème nous avons la collinéarité des points F,E et M. Ainsi en appliquant Ménélaus dans le triangle ABD nous obtenons 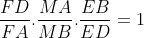 Ainsi on se doit de prouver que MA=MB mais d'après le théorème de la bissectrice intérieur il suffit de prouver que : 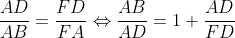 . D'autre part, puisque les deux triangles ADE et DCF sont isométriques nous avons : 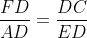 . Maintenant soit  l'angle <EDA. Nous avons : 2(alpha)=<ACB. On pose y=ED.Et ainsi : =\frac{AD}{DC}=tan(2\alpha&space;)=\frac{2tan(\alpha&space;)}{1-tan^{2}(\alpha&space;)}=\frac{2\frac{y}{AD}}{1-\frac{y^2}{AD^2}}=\frac{2y.AD}{AD^2-y^2}) ce qui donne y=ED=AC-DC. Ainsi il suffit de prouver que : 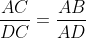 ce qui est vrai puisque les deux triangles ADC et ABC sont isométriques. Sauf erreur 
Il me parait Juste  ; Poste ton problème | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 13 Nov 2011, 12:50 Dim 13 Nov 2011, 12:50 | |
| Je n'ai pas de problèmes à proposer libre à quelqu'un de proposer un problème ( de niveau ) ... | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 13 Nov 2011, 14:10 Dim 13 Nov 2011, 14:10 | |
| - Mehdi.O a écrit:
- Je n'ai pas de problèmes à proposer libre à quelqu'un de proposer un problème ( de niveau ) ...
 Je Poste un ; J’espère qu’il soit de niveauProblème 30:Deux triangles équilatéraux sont inscrits dans un cercle de rayon r. Soit "A" l’aire de la partie contenant tous les points intérieurs aux deux triangles. Montrer que 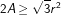 | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Lun 20 Fév 2012, 18:46 Lun 20 Fév 2012, 18:46 | |
| Bon, il est clair que l'activité de ce topic n'est plus comme avant, d'autant plus que le problème 30 est un problème de Shortlist, pour revivre je propose ce problème qui ( je crois ) sera à la portée de plusieurs forumistes, et j'espère que la participation sera plus accrue, vu que le 3ème et 4ème test approchent ainsi que les APMO, sans oublier le stage 2, on espère avoir de résultats honorants aux IMO cette année, mais la participation des forumistes n'est pas aussi active que ceux de l'an dernier. J'ai aussi eu l'idée de créer un topic afin de nous préparer de plus en plus aux phases qui nous restent cette année afin d'améliorer notre niveau et qui sera surjectif on entamera des problèmes d'inégalités, équations fonctionelles, géométrie, arithmétique et combinatoire ,et ( pourquoi pas ) pouvoir aborder des problème du niveau des olympiades internationales, j'attend vos confirmations si vous êtes intéressés. Bref, voici le problème 30 qui assez abordable pour remplacer le précédent :
Problème 30 :
Soit ABC un triangle t.q : BÂC#90, O le centre de son cercle circonscrit et (C) le cercle circonscrit de BOC. Supposons que (AB) intersecte (C) en P#B, et (AC) intersecte (C) en Q#C. Et N un point diamétralement opposé à O dans le cercle (C) ( i.e : ON est un diamètre de (C)). Montrer que : APNQ est un parallélogramme. | |
|   | | ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 21 Fév 2012, 13:00 Mar 21 Fév 2012, 13:00 | |
| jolie initiative  ! Solution au problème 30: On a: 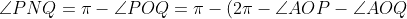) 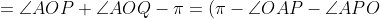+(\pi-\angle{OAQ}-\angle{AQO})-\pi) 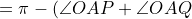-(\angle{APO}+\angle{AQO})=\pi-\angle{PAQ}-(\angle{BPO}+\angle{CQO})) 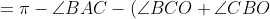=\pi-\angle{A}-(\pi-\angle{BOC})) 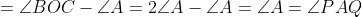 . Et on a [ON] est un diamètre dans (C), donc: 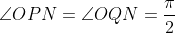 , et le triangle OBC est isocèle donc: 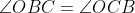 . D'où: 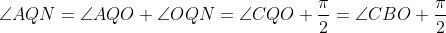 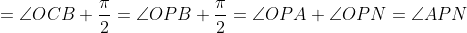 . Il s'en suit que le quadrilatère APNQ est un parallélogramme car ses angles opposés sont égaux. Je propose ce problème: Problème 31:Soit ABC un triangle, considérons le point B' tel que [BB'] est un diamètre dans le cercle circonscrit au triangle ABC, soit I le centre du cercle inscrit au triangle ABC, et M le point de contact du cercle inscrit au triangle ABC avec le côté AC, on construit les points K et L sur les côtés AB et BC respectivement tel que BK=MC et LB=AM. Montrer que (B'I) et (LK) sont perpendiculaires.
Dernière édition par ali-mes le Mar 21 Fév 2012, 20:21, édité 1 fois | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 21 Fév 2012, 13:30 Mar 21 Fév 2012, 13:30 | |
| - Mehdi.O a écrit:
- Bon, il est clair que l'activité de ce topic n'est plus comme avant, d'autant plus que le problème 30 est un problème de Shortlist, pour revivre je propose ce problème qui ( je crois ) sera à la portée de plusieurs forumistes, et j'espère que la participation sera plus accrue, vu que le 3ème et 4ème test approchent ainsi que les APMO, sans oublier le stage 2, on espère avoir de résultats honorants aux IMO cette année, mais la participation des forumistes n'est pas aussi active que ceux de l'an dernier. J'ai aussi eu l'idée de créer un topic afin de nous préparer de plus en plus aux phases qui nous restent cette année afin d'améliorer notre niveau et qui sera surjectif on entamera des problèmes d'inégalités, équations fonctionelles, géométrie, arithmétique et combinatoire ,et ( pourquoi pas ) pouvoir aborder des problème du niveau des olympiades internationales, j'attend vos confirmations si vous êtes intéressés. Bref, voici le problème 30 qui assez abordable pour remplacer le précédent :
Problème 30 :
Soit ABC un triangle t.q : BÂC#90, O le centre de son cercle circonscrit et (C) le cercle circonscrit de BOC. Supposons que (AB) intersecte (C) en P#B, et (AC) intersecte (C) en Q#C. Et N un point diamétralement opposé à O dans le cercle (C) ( i.e : ON est un diamètre de (C)). Montrer que : APNQ est un parallélogramme. Bonne initiative , la deuxième phase des olympiade pour première approche aussi,ça sera un bon entrainement  | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 21 Fév 2012, 19:22 Mar 21 Fév 2012, 19:22 | |
| - boubou math a écrit:
- Mehdi.O a écrit:
- Bon, il est clair que l'activité de ce topic n'est plus comme avant, d'autant plus que le problème 30 est un problème de Shortlist, pour revivre je propose ce problème qui ( je crois ) sera à la portée de plusieurs forumistes, et j'espère que la participation sera plus accrue, vu que le 3ème et 4ème test approchent ainsi que les APMO, sans oublier le stage 2, on espère avoir de résultats honorants aux IMO cette année, mais la participation des forumistes n'est pas aussi active que ceux de l'an dernier. J'ai aussi eu l'idée de créer un topic afin de nous préparer de plus en plus aux phases qui nous restent cette année afin d'améliorer notre niveau et qui sera surjectif on entamera des problèmes d'inégalités, équations fonctionelles, géométrie, arithmétique et combinatoire ,et ( pourquoi pas ) pouvoir aborder des problème du niveau des olympiades internationales, j'attend vos confirmations si vous êtes intéressés. Bref, voici le problème 30 qui assez abordable pour remplacer le précédent :
Problème 30 :
Soit ABC un triangle t.q : BÂC#90, O le centre de son cercle circonscrit et (C) le cercle circonscrit de BOC. Supposons que (AB) intersecte (C) en P#B, et (AC) intersecte (C) en Q#C. Et N un point diamétralement opposé à O dans le cercle (C) ( i.e : ON est un diamètre de (C)). Montrer que : APNQ est un parallélogramme. Bonne initiative , la deuxième phase des olympiade pour première approche aussi,ça sera un bon entrainement  Euh ça sera pour les 2ème BAC en quête de se préparer pour les IMO  , mais les premières sont aussi les bienvenus  bien évidemment, ( j'attends la confirmation de quelqu'un en terminale .. ) | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 21 Fév 2012, 19:24 Mar 21 Fév 2012, 19:24 | |
| | |
|   | | ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 21 Fév 2012, 20:20 Mar 21 Fév 2012, 20:20 | |
| | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 23 Fév 2012, 13:15 Jeu 23 Fév 2012, 13:15 | |
| - Mehdi.O a écrit:
- Bon, il est clair que l'activité de ce topic n'est plus comme avant, d'autant plus que le problème 30 est un problème de Shortlist, pour revivre je propose ce problème qui ( je crois ) sera à la portée de plusieurs forumistes, et j'espère que la participation sera plus accrue, vu que le 3ème et 4ème test approchent ainsi que les APMO, sans oublier le stage 2, on espère avoir de résultats honorants aux IMO cette année, mais la participation des forumistes n'est pas aussi active que ceux de l'an dernier. J'ai aussi eu l'idée de créer un topic afin de nous préparer de plus en plus aux phases qui nous restent cette année afin d'améliorer notre niveau et qui sera surjectif on entamera des problèmes d'inégalités, équations fonctionelles, géométrie, arithmétique et combinatoire ,et ( pourquoi pas ) pouvoir aborder des problème du niveau des olympiades internationales, j'attend vos confirmations si vous êtes intéressés.
Je viens de jeter un coup d'oeuil sur tes deux messages. Certes, les amateurs de matématiques actifs et qualifiés pour le deuxième stage ne sont que trois: moi (nmo), toi (Medi.O) et lui (az_360) (Cela me rapelle la leçon des pronoms en primaire). Même Dijkschneier n'est pas actif. - Mehdi.O a écrit:
- Euh ça sera pour les 2ème BAC en quête de se préparer pour les IMO
 , mais les premières sont aussi les bienvenus , mais les premières sont aussi les bienvenus  bien évidemment, ( j'attends la confirmation de quelqu'un en terminale .. ) bien évidemment, ( j'attends la confirmation de quelqu'un en terminale .. ) En effet, j'ai un penchant pour les matématiques et j'admire le défi... Le sujet que tu as déjà ouvert dans la section de terminale ne peut pas résister; son sort fatal est de mourir. Si je vais participer, il faut éviter les fautes commises dans ce topic ou bien changer notre stratégie de préparation. Je propose de faire un tournoi, à l'instar des JOPSMs, comme alternative. (Je pense que l'idée est réalisable vu le nombre médiocre des intéréssés.) Je te laisse assumer la responsabilité de l'organisation, et à bientôt... | |
|   | | momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 24 Fév 2012, 21:26 Ven 24 Fév 2012, 21:26 | |
| Salut !
Je suis tout aussi intéressé que vous (et je passe le deuxième stage ^^) ! | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  | |
| |
|   | | | | Marathon De Géométrie |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
