| | Marathon De Géométrie |  |
|
+22Oty SM.OMAR yasserito az360 boubou math momo1729 maths_lady diablo902 ali-mes SarakZit.A King Dijkschneier Bensouda majdouline Mehdi.O darkpseudo Sylphaen Sporovitch MohE nmo extrajijo Mr.Wajih 26 participants |
|
| Auteur | Message |
|---|
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 07 Juil 2013, 22:44 Dim 07 Juil 2013, 22:44 | |
| EXO 44
Let ABC be a triangle with incentre I. The angle bisectors AI, BI and CI meet [BC], [CA] and [AB] at D, E and F, respectively. The perpendicular bisector of [AD] intersects the lines BI and CI at M and N, respectively. Show that A, I, M and N lie on a circle.
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 07 Juil 2013, 23:32 Dim 07 Juil 2013, 23:32 | |
| - boubou math a écrit:
- EXO 44
Let ABC be a triangle with incentre I. The angle bisectors AI, BI and CI meet [BC], [CA] and [AB] at D, E and F, respectively. The perpendicular bisector of [AD] intersects the lines BI and CI at M and N, respectively. Show that A, I, M and N lie on a circle.
Voir le problème 27 de ce même marathon  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 07 Juil 2013, 23:56 Dim 07 Juil 2013, 23:56 | |
| Poste quelque chose  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Lun 08 Juil 2013, 00:18 Lun 08 Juil 2013, 00:18 | |
| Problème 45:
Soit ABCDE un pentagone convexe tq (BC)||(AE), et AB=BC+AE et <ABC=<CDE, soit M le milieu de CE et O le centre du cerlce circonscrit du triangle BCD, supposons que <DMO=90° , montrer que 2<BDA=<CDE | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mer 31 Juil 2013, 08:10 Mer 31 Juil 2013, 08:10 | |
| Shortlist 2010, G5. Il n'est pas très difficile et il y a de très belles solutions pour ce problème.
Pour faire avancer le marathon, voici un problème plus simple.
Problème.
Soit ABC un triangle acutangle avec angle(B) > angle(C). Soit M le mileu de BC. Soit D et E les projections orthogonales de B et C sur AC et AB respectivement. Soit K et L les mileux de ME et MD respectivement. KL coupe la droite passant par A parallèlement à BC en T. Montrer que TA=TM. | |
|
  | |
naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 | |
  | |
naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 23 Juin 2018, 13:49 Sam 23 Juin 2018, 13:49 | |
| 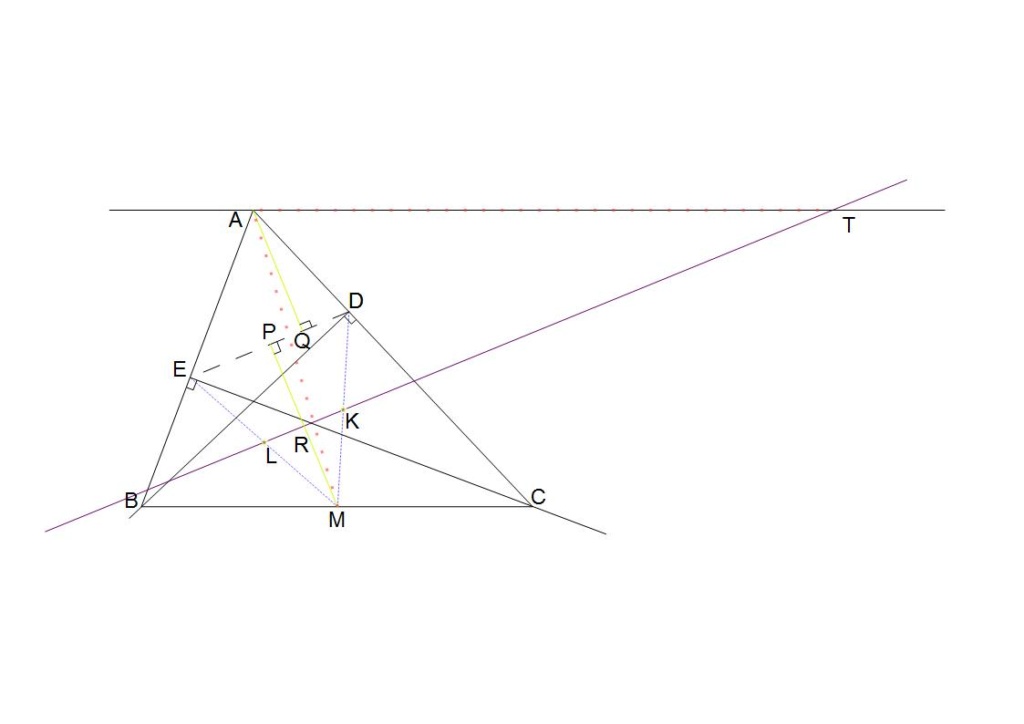 باسم الله
: بين أن AM/ [2 cos(TAM)] = TA | |
|
  | |
naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 28 Juin 2018, 04:04 Jeu 28 Juin 2018, 04:04 | |
| CDEB est un quadrilatère inscriptible car CDB = CEB. De plus, ceux-ci valent 90°, donc M est le centre du cercle circonscrit au quadrilatère cyclique. Alors le triangle MDE est isocèle de sommet M, et puisque K et L sont les milieux de ses segments [MD] et [ME], (KL) est parallèle à (ED) donc perpendiculaire à (MP) l'axe de symétrie du triangle, et passe par le milieu de la hauteur-médiane [MP], R, car KM/KD = LM/LE = 1. Aussi DME = 2 DCE = 2 DBE = 2(90°- CAB) d'une part et DMP = PME = 1/2 DME, par conséquent MR = RP = 1/2 MP = 1/2 BC/2 cos(90°- CAB) = BC/4 sin(CAB).
AED=ACB & ADE= ABC donc ADE et ABC sont deux triangles similaires. La hauteur [AQ] est alors dans leur rapport de similitude avec la hauteur [AA'] du triangle ABC, AE/AC= AD/AB= cos(BAC)= ED/BC : AQ = cos(CAB).AA' = cos(CAB).sin(CAB) AB AC /BC. Enfin, pour définir les dimensions du polygone TAQPR, il resterait à calculer :
PQ = cos(CAB).A'M = DP- DQ = DE/2- cos(ADE) AD = cos(BAC).[BC/2- cos(ABC) AB],
QAT = PMB = PME + EMB = 90°- CAB + 180°- 2 ABC = 90°- ABC+BCA.
TA = (AQ + PR) /cos(QAT) ; PT^2 = TR^2+PR^2; (TR- PQ) /TR = (AQ+ PR) /(AQ+ PR+ PQ /tan(QAT))
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  | |
| |
|
  | |
| | Marathon De Géométrie |  |
|
