Une autre

Trouver toutes les applications monotones sur $Une autre Gif$ , tel qu'il existe un nombre entier n tel que $Une autre Gif$ .

Avec $Une autre Gif.latex?f^n=%20\underset{n\;%20fois}{\underbrace{f\,%20o\,%20f\,%20o\,%20...$ .

ENJOY.

Expert sup Nombre de messages : 678 Date d'inscription : 06/06/2006

ali-mes a écrit:: Trouver toutes les applications monotones sur $Une autre Gif$ , tel qu'il existe un nombre entier n tel que $Une autre Gif$ .

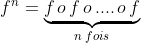Avec $Une autre Gif.latex?f^n=%20\underset{n\;%20fois}{\underbrace{f\,%20o\,%20f\,%20o\,%20...$ .

ENJOY.

Bonjour,

Notation : je note f^n la composée n fois de f.
si f est monotone f^2 est croissante et donc f^(2p) est croissante et ne peut valoir -Id.
Donc n est impair et bien sûr f est décroissante

f^n=-Id implique que f(-x)=-f(x) et f est impaire

Si f(x)>-x pour un certain x :
f(f(x))<f(-x)=-f(x)<x
f(f(f(x)))>f(x)>-x
et donc par récurrence f^(2p)(x)<x et f^(2p+1)(x)>-x et en particulier f^n(x)>-x, impossible

De même :
Si f(x)<-x pour un certain x :
f(f(x))>f(-x)=-f(x)>x
f(f(f(x)))<f(x)<-x
et donc par récurrence f^(2p)(x)>x et f^(2p+1)(x)<-x et en particulier f^n(x)<-x, impossible

Donc f(x)=-x pour tout x, ce qui constitue bien une solution (dès lors que n est impair, bien sûr)

» UNE AUTRE !!!
» Une autre
» un autre
» Une autre
» un autre exo